Polynomial division
The polynomial division , also called partial division , is a mathematical calculation method in which one polynomial is divided by another. The result is a "whole part" polynomial and possibly a remainder polynomial. The procedure is analogous to the usual division of numbers with the remainder, which is taught in schools . While smaller decimal places are temporarily ignored and the next digit of the result is guessed if necessary, the next coefficient is determined exactly by dividing the remaining highest coefficient.
General
Informal
In the following, let and natural numbers including zero ( ) and for the sake of simplicity be the quantities and always whole numbers , i.e. elements of . You now have two polynomials, for example
and
so under certain formal conditions they can be divided by one another in a similar way to whole numbers, i.e. the arithmetic problem
to solve. The result is then two polynomials: a polynomial that corresponds to the integer quotient in the number division with remainder, and a polynomial that can no longer be divided further and that corresponds to the remainder in the number division :
or in analogy to the school spelling
The method of finding this solution, consisting of and , is polynomial division .
The fact that it can not be further divided by this means that the degree of the polynomial is smaller than that of , which is why this is also required as a termination condition in the formal definition of the calculation rule ( algorithm ) . In the number division with remainder, the remainder must be smaller than the divisor . Both secondary conditions ensure that the rest of the process is clearly defined in the respective process .
In the formal definition of the procedure, some additional conditions are observed. This is because you can generally define polynomials much more broadly than has been done here for the sake of simpler explanation or you know it from school, for example. The coefficients of a polynomial can then come from any rings . But then again the coefficients of the two polynomials must not come from different rings. Therefore, one defines that the polynomials must lie in a common polynomial ring . Also, it is not enough to demand that the "highest" coefficient ( leading coefficient ) of employees must not zero. Rather, one has to demand that it must also be a unit of the ring. Or the pseudo division method described below is used.
Formally
In the case of polynomial division, two polynomials and a polynomial ring are given, with a commutative ring with and the leading coefficient of being a unit in , and it becomes the equation
for the polynomials sought and solved, in such a way that the degree of is less than that of .
Remarks
- Because the polynomials and in are uniquely determined.
- The polynomial is generally no inner join on , because as a result of the division of two polynomials in general not a single , but two polynomials in yield, and thus there is no assignment of the mold can make. However, if this is possible in individual cases, the result is a field with the polynomial division as the inverse of the polynomial multiplication .
- Is the polynomial for each arbitrary pair of two polynomials from possible, then a Euclidean ring of the polynomial function related.. This is exactly the case when there is a body.
Applications
- One application is solving higher degree equations .When a solution ( zero ) is known, polynomial division is used to decrease the degree of the equation by one. This procedure is called “splitting off a zero”.
- The polynomial division is also used in the discussion of curves with the determination of the approximation curves of a rational function .
- The polynomial division is also required for the partial fraction decomposition of rational functions.
- When calculating checksums , the polynomial division is used over the ring of integers modulo 2, see CRC polynomial .
- After the polynomial division has taken place, the same procedure can be used again for the divisor and remainder and thus calculate another remainder, and so on. A so-called residual polynomial sequence is then obtained .
calculation
Manual process
The procedure works for polynomials with integer coefficients just like the written division of integers with remainder and can be solved with the same scheme (procedure, procedure). Here are the individual steps using the example
explained:
- As with the division of whole numbers, the highest degree summand of the polynomial is eliminated first. For this purpose, the summand of the highest degree of is first divided by the summand of the highest degree of . The result is . Then with multiplied and subtracted.
- The rest remains . Its degree is not less than that of the divisor .
- In the next step, the summand of the highest degree is eliminated from this remainder, until a remainder is created in several such steps (here:) which can no longer be eliminated because its degree is smaller than the degree of the divisor .
- Further examples
algorithm
The following code fragment in BASIC shows the core of the calculation:
For i = GradZ - GradN To 0 Step -1
Quotient(i) = Zähler(i + GradN) / Nenner(GradN)
For j = GradN To 0 Step -1
Zähler(i + j) = Zähler(i + j) - Nenner(j) * Quotient(i)
Next j
Next i
For j = GradN - 1 To 0 Step -1
Rest(j) = Zähler(j)
Next j
The variable counter () is a field (array) which contains the coefficients of the numerator polynomial, so that counter (i) contains the coefficient of the power . Analogously, denominator () is another field that contains the coefficients of the denominator polynomial in the same way. The result is a polynomial which is output as quotient () and remainder (). The variables GradN and GradZ contain the respective polynomial degrees of the numerator and denominator.
In an optimized program, the inner loop would run from 0 to (GradN-1) and the results would be written back to the counter (), so that the quotient () and remainder () variables would be omitted. For the sake of simplicity, it has not been used here.
Pseudo division
The method for polynomial division described above can only be used if the leading coefficient of the divisor is a unit in the base ring. This is always the case when the base ring is a body . However, this does not always have to be the case with general basic rings. This is why a so-called pseudo division is defined that works across all integrity rings. It does not solve the above equation, but the slightly varied equation
where the polynomials and are given and a constant and polynomials and are searched for. Here, too, the degree of should again be smaller than that of .
The procedure is similar to normal polynomial division. However, in the division step not only the polynomial but also suitable factors are multiplied in order to achieve that the leading coefficients cancel each other out.
example
As an example, a pseudo division in the polynomial ring is to be carried out over the whole numbers. Be
A normal polynomial division is not possible here, since the leading coefficient of , in cannot be inverted . But we can with multiply. Now you can with pull multiplied and receives
The degree of is smaller than that of but not yet smaller than that of . If we now subtract times from this intermediate result , we get
Since the constant polynomial has a smaller degree than , we are done here. Insert backwards results
or reshaped
A sample confirms this.
algorithm
The procedure should now be illustrated by the algorithm. This recursive algorithm has as arguments two polynomials and , whereby the zero polynomial must not be, as well as the variable with respect to which the pseudodivision has to take place. The result is a triple consisting of polynomials and and a constant , so that and applies.
pseudoDivision(p, q, x) =
if d < 0
then (1, 0, p)
else (c * a, c * t + s, r) where
d = grad(p, x) - grad(q, x)
a = lcoeff(q, x)
b = lcoeff(p, x)
t = b*xd
(c,q,r) = pseudoDivision(a*p - t*q, q, x)
Here supplies the degree and the leading coefficient of a polynomial. Further improvements to the algorithm can be made, for example by omitting multiplication by x, as in the example, if it is not necessary.
Horner scheme
A polynomial division often has to be carried out using a linear factor with a leading coefficient of 1. This can be done more quickly with the Horner scheme (for the function value calculation of a polynomial). The reverse is interesting: one can also determine function values with the polynomial division. Example: with
Polynomial division returns:
After multiplying by , you can see that the remainder 22 is the function value .
Generalization to polynomial rings in several indeterminates
There is a generalized polynomial division in multivariable polynomial rings when is a field. Some compromises are accepted, such as clarity.
literature
- Peter Hartmann: Mathematics for Computer Scientists . Vieweg + Teubner, 2006, ISBN 3-8348-0096-1 , pp. 88–90 ( excerpt in the Google book search)
- Student dude mathematics II . Dudenverlag, 2004, ISBN 3-411-04275-3 , pp. 327-328
- Charles D. Miller, Margaret L. Lial, David I. Schneider: Fundamentals of College Algebra . 3rd revised edition. Scott & Foresman / Little & Brown Higher Education, 1990, ISBN 0-673-38638-4 , pp. 24-26
















![R [x]](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ce54622cb380383ab3a42441b056626ea0d2440)




![R [x] \ times R [x] \ rightarrow R [x]](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8eaa91131672964ec0929f93b15d869aac0170a)











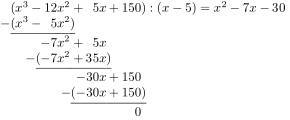
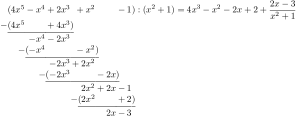



![\ mathbb {Z} [x]](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d4da3ac703cc7721ebba91a53f6752de7157124)

























![K [x_ {1}, x_ {2}, \ ldots, x_ {n}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd5197b9611cbdba8f0e65fec4069515eb9142fc)
