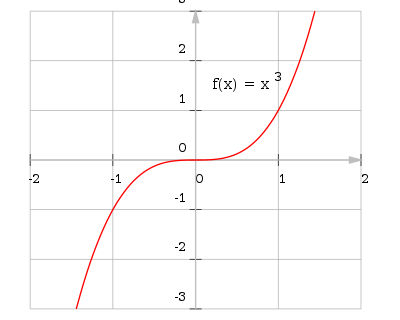
Curve discussion

Fig. 1: Plot of the function f in the section:
−1 < x <5,
0 < y <12

Fig. 2: Plot of function f in detail:
1.995 < x <2.005,
1.9999999999995 < y <2.000000000005

In mathematics, curve discussion is understood to be the investigation of the graph of a function for its geometric properties, such as points of intersection with the coordinate axes, high and low points , turning points , possibly saddle and flat points , asymptotes , behavior at infinity , etc. This information allows it to make a sketch of the graph from which all these properties characteristic of the function can be read immediately.

Today, however, it is no longer the goal of a curve discussion to support people in producing the most precise possible drawing of the graph of the function: meanwhile, every function plotter ( e.g. a graphical pocket calculator , a smartphone with the appropriate software, a spreadsheet program or computer algebra) Software ) better.

Rather, the aim of the curve discussion is

• precisely determine the coordinates of the characteristic points of the graph (only approximate values ​​can be read from a function plot);
• to prove characteristic properties such as symmetry or behavior in infinity . From a function plot one can only read statements about the depicted section of the coordinate system, e.g. As for the area , . Whether the graph of a function but z. If, for example, you “dangle” again or not, a reliable statement can only be made on the basis of a curve discussion. ${\displaystyle -6\leq x\leq 6}$ ${\displaystyle -4\leq y\leq 10}$ ${\displaystyle x=10.000}$
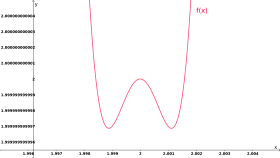
• take a closer look: an apparent local minimum can turn out to be a local maximum - given the appropriate magnification. Compare the two plots of the function

${\displaystyle f(x)=2\cdot (x-2)^{4}-0{,}000005\cdot (x-2)^{2}+2}$

in Figure 1 or Figure 2. A curve discussion always reveals such phenomena, whether they take place in the molecular domain or in astronomical dimensions: because a curve discussion does not - like a function plot - depend on the resolution.

In addition, a curve discussion can also be carried out in a very similar way for functions that depend on many variables (e.g. on , and instead of only ). A visualization of such a function in 2D or 3D is no longer possible. ${\displaystyle x_{1}}$ ${\displaystyle x_{2}}$ ${\displaystyle x_{3}}$ ${\displaystyle x}$

The importance of the curve discussion also becomes clear against the background that in decision support systems high and low points are automatic , i. H. without user interaction. If, for example, the effect of the change in a boundary condition on the variable to be optimized is to be investigated, such a system would display or graphically visualize the respective extreme value, while a value that describes the boundary condition (e.g. the level of a resource) is varied.

Domain of definition

When discussing a curve, the set of all real numbers is almost always assumed as the basic set. The maximum domain of a function is the set of all real numbers for which the function value is defined. The maximum domain of definition is the same for completely rational functions (polynomial functions) . In the case of fractional-rational functions , all real numbers with the exception of the zeros of the denominator belong to the maximum range of definition. ${\displaystyle \mathbb {R} }$ ${\displaystyle f}$ ${\displaystyle x}$ ${\displaystyle f(x)}$ ${\displaystyle \mathbb {R} }$

Examples:

• ${\displaystyle f(x)={\frac {1}{x(x-3)}};\quad D=\mathbb {R} \setminus \{0;3\}}$

The denominator of the fraction cannot be 0. Therefore the values ​​0 and 3 are excluded. ${\displaystyle x}$

• ${\displaystyle f(x)={\sqrt {25-x^{2}}};\quad D=\{x\in \mathbb {R} |-5\leq x\leq 5\}=[-5;5]}$

The radicand, i.e. the arithmetic expression under the square root , must be greater than or equal to 0. This condition is met exactly for the numbers whose amount is less than or equal to 5.

• ${\displaystyle f(x)=\ln(x+4);\quad D=\{x\in \mathbb {R} |x>-4\}=\left]-4;\infty \right[}$

The natural log function is only defined for positive arguments. So must apply. ${\displaystyle \ln }$ ${\displaystyle x>-4}$

Intersections with the coordinate axes

In order to find the zeros of a function and thus the intersections of the function graph with the axis, the solution set of the equation is calculated. The exact procedure depends on which function is being investigated. For example, if the function is given by a fraction term , the counter is set to 0 in order to obtain the zeros. ${\displaystyle f}$ ${\displaystyle x}$ ${\displaystyle f(x)=0}$ ${\displaystyle f}$

To determine the point of intersection of the function graph with the axis, 0 is used for the value. The y-axis intercept is then included . ${\displaystyle y}$ ${\displaystyle x}$ ${\displaystyle (0|f(0))}$

Symmetry properties

In answering the question of whether the graph of the given function is in any way symmetric , several cases need to be considered.

Axial symmetry with respect to the y axis

• The graph of a function is axially symmetric with respect to the -axis if and only if the following applies to any -values ​​of the domain: ${\displaystyle f}$ ${\displaystyle y}$ ${\displaystyle x}$

${\displaystyle f(-x)=f(x)}$

In the case of completely rational functions, this condition means that only even exponents occur.

Point symmetry with respect to the origin

• The graph of a function is point-symmetric with respect to the origin if and only if the following applies to any values ​​of the domain: ${\displaystyle f}$ ${\displaystyle x}$

${\displaystyle f(-x)=-f(x)}$

The graph of an entirely rational function is point-symmetric with respect to the origin if and only if only odd exponents occur.

Axis symmetry with respect to any axis

• Axial symmetry in relation to the straight line with the equation (parallel to the -axis) can be checked using the condition ${\displaystyle x=x_{0}}$ ${\displaystyle y}$

${\displaystyle f(x_{0}-h)=f(x_{0}+h).}$

Among other things, the graphs of the quadratic functions are axially symmetrical . In this case, the axis of symmetry results from the coordinate of the ( parabola ) vertex. ${\displaystyle x}$

Point symmetry with respect to any center

• The condition for point symmetry with respect to the point is ${\displaystyle (x_{0}|y_{0})}$

${\displaystyle f(x_{0}-h)+f(x_{0}+h)=2y_{0}}$

or (equivalent)

${\displaystyle f(x_{0}+h)-y_{0}=y_{0}-f(x_{0}-h).}$

The graphs of all cubic functions are point symmetric. The center of symmetry is the (only) turning point (see below).

Extreme points

→ Main article : Extreme point

To the extreme points - that is, high and low points - a continuously differentiable function to determine the first is derivative of set equal to 0, that is, the solution of the equation is calculated. All solutions to this equation are possible so-called extreme points . ${\displaystyle f}$ ${\displaystyle f}$ ${\displaystyle f'\,(x)=0}$

However, the condition is only a necessary condition for extreme points. A point with a slope of 0 could also be a saddle point . The standard example is at position 0. Although the point is not an extreme point, but a saddle point. ${\displaystyle f'\,(x)=0}$ ${\displaystyle f(x)=x^{3}}$ ${\displaystyle f'\,(0)=0}$ ${\displaystyle (0|0)}$

To prove the extreme point property, one of the sufficient conditions mentioned below is required .

Necessary condition

It is clear that the tangent to a function graph must run parallel to the -axis at an extreme point . The slope of such a tangent must therefore have the value 0. The following applies more precisely: ${\displaystyle x}$

• ${\displaystyle f}$be a real function that is defined on an open interval and is (with ) differentiable at that point . Takes at the point a relative extremum (ie a relative maximum or minimum), so true . ${\displaystyle I}$ ${\displaystyle x_{0}}$ ${\displaystyle x_{0}\in I}$ ${\displaystyle f}$ ${\displaystyle x_{0}}$ ${\displaystyle f'\,(x_{0})=0}$

At the edge of the definition range and in places where the given function cannot be differentiated, the requirements of this condition are not met. Relative extremes at such points cannot generally be determined by setting the derivative to zero.

Sufficient condition: value of the second derivative

The following sufficient condition often offers a convenient way of proving a relative extremum and at the same time determining the type (maximum or minimum). Since the second derivative is also required, it is sometimes referred to as the -Test. ${\displaystyle f''}$

• ${\displaystyle f}$be a real function that is defined in an open interval and differentiable twice. ${\displaystyle I}$

Applies in one place at the same time ${\displaystyle x_{0}\in I}$

1. ${\displaystyle f'(x_{0})=0}$ and
2. ${\displaystyle f''(x_{0})>0}$,

so at this point has a relative minimum. ${\displaystyle f}$

However, this also applies

1. ${\displaystyle f'(x_{0})=0}$ and
2. ${\displaystyle f''(x_{0})<0}$,

so has a relative maximum at this point. ${\displaystyle f}$

Example:

${\displaystyle {\begin{aligned}f(x)&=-x^{2}+8x\\f'(x)&=-2x+8\\f''(x)&=-2\end{aligned}}}$

Setting the first derivative ( ) to zero gives . Inserting into the second derivative gives (condition for a relative maximum). The graph of has exactly one extreme point, namely a high point with coordinate 4. ${\displaystyle -2x+8=0}$ ${\displaystyle x=4}$ ${\displaystyle f''(4)=-2<0}$ ${\displaystyle f}$ ${\displaystyle x}$

Occasionally both and . In this case, further examinations are necessary to decide whether or not there is an extreme point. Specifically, this means that a derivative must be made until a derivative of even order - fourth, sixth, ... order - is available, which is not equal to 0 at this point. ${\displaystyle f'(x_{0})=0}$ ${\displaystyle f''(x_{0})=0}$

The simplest example is . The first three derivatives at the point , that is , and each have the value 0. Only the fourth derivative enables the detection of the extremum. The positive sign shows that there is a relative minimum at this point . ${\displaystyle f(x)=x^{4}}$ ${\displaystyle x_{0}=0}$ ${\displaystyle f'(0)}$ ${\displaystyle f''(0)}$ ${\displaystyle f'''(0)}$ ${\displaystyle f^{(4)}(x)=24}$ ${\displaystyle f^{(4)}(0)=24\neq 0}$ ${\displaystyle x_{0}=0}$

In rare cases this more general criterion also fails, namely when all derivatives at the point are equal to 0. ${\displaystyle x_{0}}$

Sufficient condition: sign of the first derivative

Another method for verifying the extreme point property does not require the calculation of the second derivative. It is examined whether the sign of the first derivative changes at the point under consideration . This method, sometimes referred to as the sign change method (VZW method), can be clearly interpreted as follows: ${\displaystyle f'(x)}$ ${\displaystyle x_{0}}$

If you run through the function graph in the vicinity of a high point from left to right, the appearance of this curve can be described as follows:

1. The function graph rises to the left of the high point. The slope is positive.
2. At the high point itself, the tangent runs horizontally. The slope is 0.
3. The function graph falls to the right of the high point. The slope is negative.

The same applies to lows, only the other way round.

• ${\displaystyle f}$be a real function that is defined and differentiable in an open interval . ${\displaystyle I}$

Applies in one place at the same time ${\displaystyle x_{0}\in I}$

1. ${\displaystyle f'(x_{0})=0}$,
2. ${\displaystyle f'(x)<0}$for and ${\displaystyle x<x_{0},\,x\in I}$
3. ${\displaystyle f'(x)>0}$for , ${\displaystyle x>x_{0},\,x\in I}$

so at this point has a relative minimum. ${\displaystyle f}$

Applies in one place at the same time ${\displaystyle x_{0}\in I}$

1. ${\displaystyle f'(x_{0})=0}$,
2. ${\displaystyle f'(x)>0}$for and ${\displaystyle x<x_{0},\,x\in I}$
3. ${\displaystyle f'(x)<0}$for , ${\displaystyle x>x_{0},\,x\in I}$

so has a relative maximum at this point. ${\displaystyle f}$

Example:

${\displaystyle f(x)=x^{4}}$

${\displaystyle f'(x)=4x^{3}}$

Setting the derivative to zero ( ) provides a point with a horizontal tangent and thus a candidate for an extreme point . In the VZW test, values ​​that are smaller or larger than 0 are considered. ${\displaystyle 4x^{3}=0}$ ${\displaystyle x=0}$ ${\displaystyle x}$

${\displaystyle f'(x)=4x^{3}<0}$ For ${\displaystyle x<0}$

${\displaystyle f'(x)=4x^{3}>0}$ For ${\displaystyle x>0}$

shows that there is a low point.

One problem with the VZW test is that the sign of the derivative does not have to be determined for a single digit, but for an entire interval. In school mathematics one therefore often only determines the sign for a single digit of the interval and concludes from this that this sign applies to the entire interval. This procedure is permitted if the function is continuously differentiable in the interval . ${\displaystyle I}$

Historical side note: The determination of the extremes from the tangent slope was first proposed by Fermat in a letter to Descartes - before the term derivation existed.

Turning points

→ Main article : turning point

Turning points are those points at which the given function graph changes between a left and right curve. The type of curvature can be recognized - under certain conditions - from the sign of the second derivative . A positive sign indicates a left curve, a negative sign indicates a right curve. In the standard procedure for determining the turning points, the second derivative is therefore equal to 0. The solutions of the equation (see necessary condition) are possible turning points . With one of the sufficient conditions listed below, one can then prove that a turning point actually exists. ${\displaystyle f''(x)}$ ${\displaystyle f''(x)=0}$

At Bavarian vocational high schools , turning points are defined as extreme points of the first derivation.

Necessary condition

• ${\displaystyle f}$be a real function, which is defined in an open interval and continuously differentiable twice. Does the graph of at the site of a turning point, it shall ${\displaystyle I}$ ${\displaystyle f}$ ${\displaystyle x_{0}\in I}$

${\displaystyle f''(x_{0})=0.}$

Sufficient condition: value of the third derivative

The latter condition is not sufficient for further investigations to be carried out. A sufficient condition often used to prove turning points is based on the third derivative:

• ${\displaystyle f}$be a real function that is defined in an open interval and three times differentiable. Applies in one place at the same time ${\displaystyle I}$ ${\displaystyle x_{0}\in I}$

1. ${\displaystyle f''(x_{0})=0}$ and
2. ${\displaystyle f'''(x_{0})\neq 0,}$

then the graph of has at the point a turning point. ${\displaystyle f}$ ${\displaystyle x_{0}}$

Sufficient condition: sign of the second derivative

If, in addition to the second derivative, the third derivative is also 0 at this point, the last-mentioned criterion fails. In this case one examines whether the sign of the second derivative changes. For this purpose one chooses a value smaller and one larger than the zero of the second derivative (i.e. the coordinate of the turning point). These two values ​​are inserted into the second derivative. If the signs of the values ​​of the second derivative differ at these points, there is a turning point. If the sign changes from minus to plus, then it is a turning point with a transition from a right to a left curve. If the sign changes from plus to minus, it is a turning point with a transition from a left to a right curve. ${\displaystyle x_{0}}$ ${\displaystyle x_{0}}$ ${\displaystyle x}$

• ${\displaystyle f}$be a real function that is defined in the open interval and differentiable twice. Applies at the same time ${\displaystyle I}$ ${\displaystyle x_{0}\in I}$

1. ${\displaystyle f''(x_{0})=0}$,
2. ${\displaystyle f''(x)<0}$for , and ${\displaystyle x<x_{0}}$ ${\displaystyle x\in I}$
3. ${\displaystyle f''(x)>0}$for , ${\displaystyle x>x_{0}}$ ${\displaystyle x\in I}$

or at the same time

1. ${\displaystyle f''(x_{0})=0}$,
2. ${\displaystyle f''(x)>0}$for , and ${\displaystyle x<x_{0}}$ ${\displaystyle x\in I}$
3. ${\displaystyle f''(x)<0}$for , , ${\displaystyle x>x_{0}}$ ${\displaystyle x\in I}$

then the graph of has at the point a turning point. ${\displaystyle f}$ ${\displaystyle x_{0}}$

Special case: saddle points

A turning point with a horizontal tangent is called a saddle point or a terrace point. For him, and , as in the example of the function with the equation, apply ${\displaystyle f'(x)=0}$ ${\displaystyle f''(x)=0}$

${\displaystyle f(x)={x^{3}}}$

at the point . ${\displaystyle x=0}$

However, this is not a sufficient criterion, it can and will be without a saddle point occurring, as shown in the following example: ${\displaystyle f'(x)=0}$ ${\displaystyle f''(x)=0}$

${\displaystyle f(x)={x^{4}}}$

Only when it is is a saddle point proven; More generally, the following applies: There is a turning point if the degree of the first derivative other than 0 is odd; if the degree is even, it is an extreme. In cases like ${\displaystyle f'''\neq 0}$

${\displaystyle f(x)={x^{5}}}$

However, the third derivative is useless because it also disappears at the 0 position. The sign change criterion helps here.

Poles

In fractional-rational functions, a pole is present at a point if the denominator polynomial has a zero at and the numerator polynomial has a zero of a lower order at or no zero at . ${\displaystyle p}$ ${\displaystyle p}$ ${\displaystyle p}$ ${\displaystyle p}$

If both the numerator and the denominator polynomial have a zero and the order of the zero in the numerator polynomial is not smaller than that of the denominator polynomial, there is a continuously eliminable definition gap . ${\displaystyle p}$

In university mathematics there are other types of undefined positions that are neither clearable gaps nor pole positions.

gap

In the case of fractional-rational functions, there is a continuously correctable definition gap at one point if not only a zero of the denominator but also a zero of the numerator is of at least the same degree. In this case, the associated linear factor can be shortened. ${\displaystyle x_{0}}$ ${\displaystyle x_{0}}$ ${\displaystyle (x-x_{0})}$

Example: has a definable gap in the definition at this point . By reducing the factor : ${\displaystyle {\tfrac {x^{2}-4}{x-2}}}$ ${\displaystyle x=2}$ ${\displaystyle (x-2)}$

${\displaystyle {\frac {x^{2}-4}{x-2}}={\frac {(x+2)\cdot (x-2)}{x-2}}=x+2}$   (for ). ${\displaystyle x\neq 2}$

Another way to test whether there is a continuously correctable definition gap at the point is to calculate the limit value . If this limit exists and is finite, then there is a continuously recoverable gap. ${\displaystyle x_{0}}$ ${\displaystyle \lim _{x\rightarrow x_{0}}f(x)}$

Behavior in infinity

In order to find out the behavior at infinity, the function value of the function is examined when it increases beyond all limits, i.e. goes against : ${\displaystyle f(x)}$ ${\displaystyle x}$ ${\displaystyle \infty }$

${\displaystyle \lim _{x\to \infty }f(x)\;;}$

The same for . ${\displaystyle -\infty }$

Overview of criteria

Is discussed ${\displaystyle f\colon x\mapsto f(x)}$
Investigation aspect	criteria
Zero	${\displaystyle f(x_{N})=0\,}$
Extreme point	${\displaystyle f'(x_{E})=0\,}$	(necessary criterion)
	${\displaystyle f'(x_{E})=0\land f''(x_{E})\neq 0}$	(sufficient criterion)
Minimum position	${\displaystyle f'(x_{E})=0\,}$	(necessary criterion)
	${\displaystyle f'(x_{E})=0\land f''(x_{E})>0}$	(sufficient criterion)
Maximum position	${\displaystyle f'(x_{E})=0\,}$	(necessary criterion)
	${\displaystyle f'(x_{E})=0\land f''(x_{E})<0}$	(sufficient criterion)
Turning point	${\displaystyle f''(x_{W})=0\,}$	(necessary criterion)
	${\displaystyle f''(x_{W})=0\land f'''(x_{W})\neq 0}$	(sufficient criterion)
Saddle position	${\displaystyle f'(x_{W})=0\land f''(x_{W})=0}$	(necessary criterion)
	${\displaystyle f'(x_{W})=0\land f''(x_{W})=0\land f'''(x_{W})\neq 0}$	(sufficient criterion)
Behavior in infinity	${\displaystyle \lim _{x\to \infty }f(x)}$,	${\displaystyle \lim _{x\to -\infty }f(x)}$
symmetry
Axis symmetry to the coordinate axis	${\displaystyle f(x)=f(-x)\,}$
Point symmetry to the origin of coordinates	${\displaystyle -f(x)=f(-x)\,}$
monotony
increasing / strictly increasing	${\displaystyle f'(x)\geq 0}$	${\displaystyle f'(x)>0\,}$
falling / strictly falling	${\displaystyle f'(x)\leq 0}$	${\displaystyle \,f'(x)<0}$
curvature
Left curve / convex arch (open at the top)	${\displaystyle f''(x)>0\,}$
Right curve / concave arch (open at the bottom)	${\displaystyle f''(x)<0\,}$
periodicity	${\displaystyle f(x+p)=f(x)\,}$
Is discussed ${\displaystyle f\colon x\mapsto {\frac {p(x)}{q(x)}}}$
Investigation aspect	criteria
Domain of definition	${\displaystyle \mathbb {D} =\mathbb {R} \setminus \lbrace x_{0}\mid q(x_{0})=0\rbrace }$
Pole position	${\displaystyle q(x_{p})=0\,}$	(necessary criterion)
	${\displaystyle q(x_{p})=0\land p(x_{p})\neq 0}$	(sufficient criterion)

Example: a completely rational function

Graphs of the functions f (black), f '(red) and f ' '(blue)

The function to be examined is:

${\displaystyle f(x)=3x^{3}-5x^{2}+8}$

The graph of the function is shown in black in the picture, and the first (red) and second (blue) derivatives are entered: ${\displaystyle f}$

zeropoint

The zero can be found by trial and error (for example by preparing a table of values ) or according to the Gaussian inference that every integer zero must be a divisor of the absolute term 8 . If there were no such easily recognizable zero, Cardano's formula could be used for equations of the 3rd degree or Newton's approximation method . ${\displaystyle x=-1}$

The linear factor belongs to the zero . To find the other zeros, a polynomial division is carried out using this linear factor and the result is set to 0. The result is a little quicker with the Horner scheme . This way, the degree of the equation is reduced by 1. ${\displaystyle x=-1}$ ${\displaystyle (x-(-1))=(x+1)}$

${\displaystyle (3x^{3}-5x^{2}+8):(x+1)=3x^{2}-8x+8}$

The new equation has no solution. is consequently the only real zero. ${\displaystyle 3x^{2}-8x+8=0}$ ${\displaystyle x=-1}$

Extreme points

The first derivative function is

${\displaystyle f'(x)=9x^{2}-10x=9x(x-{\tfrac {10}{9}})\,}$.

This has zeros at and at . This means that there can be extreme points here. ${\displaystyle x_{1}=0}$ ${\displaystyle x_{2}={\tfrac {10}{9}}}$

The second derivative function

${\displaystyle f''(x)=18x-10\,}$

has the function values ​​in the above places

${\displaystyle f''(x_{1})=18\cdot 0-10=-10<0}$

or.

${\displaystyle f''(x_{2})=18\cdot {\tfrac {10}{9}}-10=10>0.}$

Therefore, the function graph has a high point (first derivative equal to 0, second derivative negative) and a low point (first derivative equal to 0, second derivative positive). The coordinates of the two extreme points result from inserting the coordinates in . ${\displaystyle x_{1}}$ ${\displaystyle x_{2}}$ ${\displaystyle y}$ ${\displaystyle x}$ ${\displaystyle f(x)}$

${\displaystyle {\begin{aligned}y_{1}&=f(0)=3\cdot 0^{3}-5\cdot 0^{2}+8=8\\y_{2}&=f({\tfrac {10}{9}})=3\cdot \left({\tfrac {10}{9}}\right)^{3}-5\cdot \left({\tfrac {10}{9}}\right)^{2}+8=5{\tfrac {229}{243}}\end{aligned}}}$

High point: ${\displaystyle (0|8)}$

Low point: ${\displaystyle ({\tfrac {10}{9}}|5{\tfrac {229}{243}})}$

Turning points

To determine the turning points, the second derivative is set to zero: ${\displaystyle f''(x)=18x-10}$

${\displaystyle 18x-10=0}$

The only solution to this equation is . The third derivative can be used to confirm that there is indeed a turning point . Because of ${\displaystyle x_{3}={\tfrac {5}{9}}}$ ${\displaystyle f'''(x)=18}$

${\displaystyle f'''(x_{3})=f'''({\tfrac {5}{9}})=18\neq 0}$

the turning point property is secured. The coordinate of the turning point results in ${\displaystyle y}$

${\displaystyle y_{3}=f(x_{3})=3\cdot \left({\tfrac {5}{9}}\right)^{3}-5\cdot \left({\tfrac {5}{9}}\right)^{2}+8=6{\tfrac {236}{243}}.}$

Turning point: ${\displaystyle ({\tfrac {5}{9}}|6{\tfrac {236}{243}})}$

Poles and behavior in infinity

There are no poles in polynomials. As a polynomial of odd order (highest exponent at ) the function goes against or , if against or goes. ${\displaystyle x^{3}}$ ${\displaystyle +\infty }$ ${\displaystyle -\infty }$ ${\displaystyle x}$ ${\displaystyle +\infty }$ ${\displaystyle -\infty }$

Example: fractional-rational function

Graphs of the functions f (red), f '(blue) and f ' '(green)

The function is given by the equation

${\displaystyle {f(x)}={\frac {x^{3}-4x^{2}+4x}{4x^{2}-8x+4}}}$

Domain of definition

The function is only defined where the denominator is not equal to 0. Examining the denominator for zeros gives:

${\displaystyle 4x^{2}-8x+4=0}$

${\displaystyle x^{2}-2x+1=0}$

${\displaystyle x=1+{\sqrt {1-1}}=1}$ or ${\displaystyle x=1-{\sqrt {1-1}}=1}$

The quadratic equation has a double solution at . The denominator only becomes 0. The domain is consequently ${\displaystyle x=1}$ ${\displaystyle x=1}$

${\displaystyle \mathbb {D} =\mathbb {R} \setminus \{1\},}$

the set of real numbers, with the exception of 1. The denominator can - broken down into linear factors - as

${\displaystyle 4(x-1)(x-1)}$ or ${\displaystyle 4(x-1)^{2}}$

to be written.

zeropoint

The condition for zeros is . It is sufficient for the numerator to become 0 as long as the denominator does not also become 0. Examination of the counter for zeros shows: ${\displaystyle f(x_{N})=0\,}$

${\displaystyle x^{3}-4x^{2}+4x=0}$

${\displaystyle x(x^{2}-4x+4)=0}$

${\displaystyle x=0}$or or ${\displaystyle x=2+{\sqrt {4-4}}=2}$ ${\displaystyle x=2-{\sqrt {4-4}}=2}$

The counter has a single zero at and a double at . Both places are within the definition range. so has the zeros as well . ${\displaystyle x=0}$ ${\displaystyle x=2}$ ${\displaystyle f(x)}$ ${\displaystyle x_{1}=0}$ ${\displaystyle x_{2}=x_{3}=2}$

The counter can - broken down into linear factors - as

${\displaystyle x(x-2)(x-2)=x(x-2)^{2}}$

to be written.

As part of the school mathematics is often considered important that in each of the index for "zero" is to written . ${\displaystyle x}$ ${\displaystyle N}$ ${\displaystyle x_{N}\,}$

Poles

At this point the denominator has a double zero position without the numerator becoming 0 at the same time. So there is a pole at . If the numerator should also be 0, the order of the denominator zero for a pole must be greater than the order of the numerator zero. ${\displaystyle x=1}$ ${\displaystyle x=1}$

If the denominator of a fractional-rational function equals 0 at one point , the function is not defined at this point. If the denominator is 0, but the numerator is not 0, the function has a pole at this point ("infinity point"). ${\displaystyle x=a}$

symmetry

The graph of the function is examined for symmetry at this point. Often there is only an examination for axis symmetry to the -axis (condition ) and for point symmetry to the origin of the coordinate system (condition ). ${\displaystyle y}$ ${\displaystyle f(-x)=f(x)}$ ${\displaystyle f(-x)=-f(x)}$

In the example, in

${\displaystyle {f(x)}={{x^{3}-4x^{2}+4x} \over {4x^{2}-8x+4}}}$

${\displaystyle x}$replaced by . After the multiplication results ${\displaystyle -x}$

${\displaystyle {f(-x)}={{(-x)^{3}-4(-x)^{2}+4(-x)} \over {4(-x)^{2}-8(-x)+4}}={{-x^{3}-4x^{2}-4x} \over {4x^{2}+8x+4}}}$.

Since neither with nor with corresponds, the graph of is neither axially symmetric to the -axis nor point symmetric to the origin. ${\displaystyle f(-x)}$ ${\displaystyle f(x)}$ ${\displaystyle -f(x)}$ ${\displaystyle f}$ ${\displaystyle y}$

The investigation of axial symmetry with respect to any axis or point symmetry with respect to any point is somewhat more difficult. Axial symmetry can be excluded because of and . As a center of symmetry (point symmetry), at most the point of intersection of the asymptotes (see below), i.e. the point, would come into question. But since, for example, the points and are not symmetrical with respect to each other, the graph is also not point-symmetrical. ${\displaystyle \textstyle \lim _{x\to -\infty }f(x)=-\infty }$ ${\displaystyle \textstyle \lim _{x\to \infty }f(x)=+\infty }$ ${\displaystyle (1|-{\tfrac {1}{4}})}$ ${\displaystyle (0|0)}$ ${\displaystyle (2|0)}$ ${\displaystyle (1|-{\tfrac {1}{4}})}$

Derivatives

The derivatives of

${\displaystyle {f(x)}={{x(x-2)^{2}} \over {4(x-1)^{2}}}.}$

The representation in linear factors is more useful because it simplifies the factoring out and shortening. This results first

${\displaystyle {\begin{aligned}{f'(x)}&={{(2x(x-2)+(x-2)^{2})4(x-1)^{2}-x(x-2)^{2}\cdot 8(x-1)} \over {16(x-1)^{4}}}\\&={{(2x(x-2)+(x-2)^{2})(x-1)-2x(x-2)^{2}} \over {4(x-1)^{3}}}\\&={{(x-2)((2x+(x-2))(x-1)-2x(x-2))} \over {4(x-1)^{3}}}\\&={{(x-2)((3x-2)(x-1)-2x(x-2))} \over {4(x-1)^{3}}}\\&={{(x-2)(3x^{2}-3x-2x+2-2x^{2}+4x)} \over {4(x-1)^{3}}}\\&={{(x-2)(x^{2}-x+2)} \over {4(x-1)^{3}}}\end{aligned}}}$

for the first derivative. Then the second

${\displaystyle {\begin{aligned}{f''(x)}&={{((x-2)(2x-1)+(x^{2}-x+2))(x-1)^{3}-(x-2)(x^{2}-x+2)\cdot 3(x-1)^{2}} \over {4(x-1)^{6}}}\\&={{((x-2)(2x-1)+(x^{2}-x+2))(x-1)-3(x-2)(x^{2}-x+2)} \over {4(x-1)^{4}}}\\&={{(2x^{2}-x-4x+2+x^{2}-x+2)(x-1)-(3x-6)(x^{2}-x+2)} \over {4(x-1)^{4}}}\\&={{(3x^{2}-6x+4)(x-1)-(3x^{3}-3x^{2}+6x-6x^{2}+6x-12)} \over {4(x-1)^{4}}}\\&={{3x^{3}-3x^{2}-6x^{2}+6x+4x-4-3x^{3}+3x^{2}-6x+6x^{2}-6x+12} \over {4(x-1)^{4}}}\\&={{-2x+8} \over {4(x-1)^{4}}}\\&={{4-x} \over {2(x-1)^{4}}}\end{aligned}}}$

and the third derivative

${\displaystyle {\begin{aligned}{f'''(x)}&={-{(x-1)^{4}-(4-x)4(x-1)^{3}} \over {2(x-1)^{8}}}\\&={-{(x-1)-4(4-x)} \over {2(x-1)^{5}}}\\&={-{x+1-16+4x} \over {2(x-1)^{5}}}\\&={{3x-15} \over {2(x-1)^{5}}}\end{aligned}}}$

educated.

Extreme points

For this must be. It is enough to examine the zeros of the counter: ${\displaystyle f'(x)=0\,}$

${\displaystyle {(x-2)(x^{2}-x+2)}=0\,}$

has the solution . The second bracket has no real solutions. is within the definition range. The function value at this point is because there is a zero here. The second derivative is at this point , so it is a low point at (2/0) . ${\displaystyle x=2}$ ${\displaystyle x=2}$ ${\displaystyle f(2)=0\,}$ ${\displaystyle f''(2)=1>0\,}$

Turning points

The turning point is determined by setting the second derivative equal to 0. From this approach follows . Substituting this value into the third derivative gives . So there is indeed a turning point. The calculation of finally results in the coordinate . The turning point we are looking for is thus . ${\displaystyle x_{W}=4}$ ${\displaystyle f'''(4)=-{\tfrac {1}{162}}\neq 0}$ ${\displaystyle f(4)}$ ${\displaystyle y}$ ${\displaystyle y_{W}={\tfrac {4}{9}}}$ ${\displaystyle (4|{\tfrac {4}{9}})}$

Asymptotes

At the pole, that is, at , there is a vertical asymptote . Since the degree of the counter (3) to 1 is greater than that of the denominator (2), to go for up . The difference indicates that the graph will asymptotically approach a linear function (straight line). The straight line equation follows by polynomial division : ${\displaystyle x=1}$ ${\displaystyle f(x)}$ ${\displaystyle \infty }$ ${\displaystyle x}$ ${\displaystyle \infty }$ ${\displaystyle 3-2=1}$

${\displaystyle (x^{3}-4x^{2}+4x):(4x^{2}-8x+4)={{1 \over 4}x-{1 \over 2}+{{-1x+2} \over {4x^{2}-8x+4}}}}$

For against , the last term approaches 0. The equation of the asymptote is thus ${\displaystyle x}$ ${\displaystyle \infty }$

${\displaystyle {a(x)}={{1 \over 4}x-{1 \over 2}}}$

General:

• If the denominator degree is greater than the numerator degree, the asymptote is the -axis. ${\displaystyle x}$
• If the denominator degree is equal to the numerator degree, the asymptote is parallel to the -axis. ${\displaystyle x}$
• If the denominator degree is 1 smaller than the numerator degree, the asymptote is skewed.
• If the denominator degree is more than 1 smaller than the numerator degree, the asymptote is not a straight line, but curved. (Asymptotic approximation curve)

Didactic questions

In mathematics didactics , it has been discussed since the 1990s at the latest, to what extent the discussion of curves has been overtaken by the availability of graphical pocket calculators and dedicated software ( function plotter ).

It is criticized that the curve discussion is a purely computational routine that gives little understanding. On the other hand, it is for this very reason that it is comparatively popular among weaker pupils and students as an exam subject to be prepared relatively safely.

In the central Abitur exams it has therefore become established that such schematic tasks are only very rarely given. More popular are dressed-up tasks or tasks in which contextual knowledge is queried, for example about the relationships between the derivative function and the output function.

A didactic method is described in area classification .

literature

• Harald Scheid , Wolfgang Schwarz: Elements of linear algebra and analysis . Springer, 2009, ISBN 9783827422552 , pp. 316–322
• Harro Heuser : Textbook of Analysis. Part 1. Vieweg + Teubner, Wiesbaden 1980, ISBN 3-519-02221-4 , pp. 293-295
• Curve discussion In: Schülerduden - Mathematics II . Bibliographisches Institut & FA Brockhaus, 2004, ISBN 3-411-04275-3 , pp. 235–241.
• Mathematics - Analysis . Cornelsen, 2002, ISBN 978-3-464-57216-0 , pp. 108-142

Web links

• Understandable text for the curve discussion
• Exemplary curve discussions
• Online calculator for curve discussion with calculation path

Individual evidence

1. ↑ Friedrich Barth a. a. (Ed.): Mathematical formulas and definitions . P. 64
2. ↑ Steffen Hahn, Susanne Prediger: Presentation-oriented curve discussion - A plea for the qualitative (PDF; 306 kB) University of Bremen, on mathematik.uni-dortmund.de