Point symmetry
The point symmetry, also inversion symmetry or central symmetry, is a property of a figure in geometry . A figure is point-symmetrical if it is mapped onto itself by being reflected at a point of symmetry .
definition
A (flat) geometrical figure (for example a square) is called point-symmetric if there is a point reflection that depicts this figure on itself. The point at which this reflection occurs is called the center of symmetry .
Point reflection as rotation (and reflection)
In the plane (two-dimensional Euclidean space ) the point reflection corresponds to a rotation of the geometric figure by 180 ° around the point of symmetry. Here point symmetry is a special case of rotational symmetry . In three-dimensional Euclidean space, the point reflection corresponds to a rotation of the geometric figure by 180 ° around the point of symmetry and subsequent reflection through the point of symmetry on the plane perpendicular to the axis of rotation.
More generally applies:
In 2N-dimensional space, the point reflection corresponds to N rotations of 180 ° each. The axes of rotation are perpendicular to each other in pairs and intersect at the point of symmetry.
In the 2N + 1-dimensional space, the point reflection corresponds to N rotations of 180 ° and subsequent reflection. The axes of rotation are perpendicular to each other in pairs and intersect at the point of symmetry. The point of symmetry is also on the mirror plane and all axes of rotation are perpendicular to the mirror plane.
Examples
- With a square there is point symmetry (in itself) if and only if it is a parallelogram . The center of symmetry is then the intersection of the diagonals. As special cases of the parallelogram, rectangle , diamond and square are point-symmetrical.
- Each circle is (in itself) point-symmetrical with respect to its center.
- Two circles with the same radius are point-symmetrical to one another. The center of symmetry is the midpoint of the line connecting the two circle centers.
- Several centers of symmetry can only exist if the figure is not restricted . The simplest example is the straight line. It even has an infinite number of centers of symmetry.
- A triangle is never point symmetric. However, two triangles can be point-symmetrical to one another.
- A regular polygon with an even number of corners is point-symmetric.
Point symmetry of function graphs
overview
A common task in school mathematics is to prove that the graph of a given function is point-symmetric with the domain of definition and with real function values.
If there is a point so the equation for the function
holds for all , then the function is point-symmetric with respect to the point The mentioned condition is with
equivalent, as the substitution shows. In the special case of point symmetry in relation to the origin , this equation is simplified to
If it is valid for all , then there is point symmetry with respect to the coordinate origin. Then the function is called an odd function .
Examples
Point symmetry in relation to the origin of coordinates
Given the function Then:
So the function graph is point-symmetric with the center of symmetry at the origin (0,0).
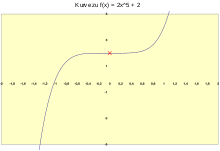
Point symmetry with respect to the point (0,2)
Given the function Select and then:
Hence the function graph is point symmetric with respect to the point and it holds
This procedure does not help to determine the point of symmetry . In most cases, however, it is sufficient to draw the function graph and derive an assumption about the symmetry point from it.
Individual evidence
- ↑ Arthur Schoenflies: Crystal systems and crystal structure . Teubner, Leipzig 1891 (XII, 638 p., Online resources ).
- ↑ Spektrum.de: Inversion Symmetry. Retrieved March 5, 2020 .
- ↑ Meyer's large pocket dictionary in 24 volumes. BI-Taschenbuchverlag, 1992, Volume 21, p. 258.
- ^ Arnfried Kemnitz: Mathematics at the beginning of the course . Vieweg + Teubner, Wiesbaden 2011, ISBN 978-3-8348-8258-5 , pp. 144 .