Euclidean space
In mathematics , the Euclidean space is first of all the “space of our intuition” as it is described in Euclid's elements by axioms and postulates (cf. Euclidean geometry ). Up until the 19th century it was assumed that this described the physical space that surrounds us . The addition “Euclidean” became necessary after more general spatial concepts (e.g. hyperbolic space , Riemannian manifolds ) had been developed in mathematics and it became apparent in the context of the special and general theory of relativity that other spatial concepts are required to describe space in physics ( Minkowski space , Lorentz manifold ).
Over time, Euclid's geometry was refined and generalized in several ways:
- axiomatically by Hilbert ( see Hilbert's system of axioms of Euclidean geometry ),
- as a Euclidean vector space (a vector space defined by a scalar product ),
- as Euclidean point space (an affine space modeled over a Euclidean vector space),
- as a coordinate space with the standard scalar product .
When Euclidean space is mentioned, any of these definitions can be meant, or a higher-dimensional generalization. The two-dimensional Euclidean space is also called the Euclidean plane . In this two-dimensional case, the term is more generalized in synthetic geometry : Euclidean planes can be defined there as affine planes over a more general class of bodies, the Euclidean bodies . These bodies are (depending on your opinion) partial bodies or isomorphic to partial bodies of
Euclidean space differs from affine space in that lengths and angles can be measured. One therefore draws up the images that contain lengths and angles. These are traditionally called congruence maps , other terms are movements and isometrics .
In the non-Euclidean spaces , such as the hyperbolic and elliptical spaces, the axiom of parallels does not apply.
Euclidean vector spaces
From Euclidean intuition space to Euclidean vector space
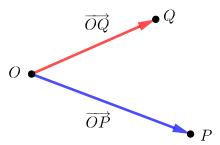
In analytic geometry , Euclidean space is assigned a vector space . One possibility to do this is to take the amount of parallel displacements (translations), provided with the execution as an addition. Each shift can be described by an arrow that connects a point with its image point. Two arrows, which are parallel in the same direction and have the same length, describe the same displacement. Two such arrows are called equivalent and the equivalence classes are called vectors .
If you select a point in Euclidean space as a reference point ( origin ), you can assign each point its position vector , the vector that is represented by an arrow from the origin to the point . In this way one gets a one-to-one relationship between the Euclidean space and the associated Euclidean vector space and can thus identify the original Euclidean space with the Euclidean vector space. However, this identification is not canonical, but depends on the choice of origin.
One can now also transfer the length and angle measurements from Euclidean space to vectors as the length of the associated arrows and angles between them. In this way a vector space with a scalar product is obtained . The scalar product is characterized by the fact that the product of a vector with itself is the square of its length . The formula results from the calculation laws for scalar products, the binomial formulas and the cosine law (applied to a triangle whose sides correspond to the vectors , and )
- .
Here denotes the angle between the vectors and .
General term
Proceeding from this, one calls every real vector space with a scalar product (any finite dimension ) a Euclidean vector space . The above formula is then used to define the length ( norm ) of a vector and the angle between vectors. Two vectors are orthogonal if their scalar product is zero. Every three-dimensional Euclidean vector space is isometrically isomorphic to the vector space of the arrow classes. Every -dimensional Euclidean vector space is isometrically isomorphic to the coordinate vector space (see below). Euclidean vector spaces of the same dimension are therefore indistinguishable. This justifies one to designate each such as the Euclidean vector space of the dimension . Some authors also use the term Euclidean space for infinite-dimensional real vector spaces with a scalar product, some also for complex vector spaces with a scalar product, cf. Dot product space .
Lengths, angles, orthogonality and orthonormal bases
As soon as one has provided a real vector space with a scalar product, one can transfer the metric concepts of the Euclidean intuition space to this. The length (the norm , the amount ) of a vector is then the root of the scalar product of the vector with itself:
- .
Two vectors are orthogonal (or perpendicular ) to each other if their scalar product is zero:
- .
The (non-oriented) angle between two vectors is defined using the above formula
- ,
so
- .
A vector is called a unit vector if it has the length 1. A basis made up of unit vectors that are pairwise orthogonal is called an orthonormal basis . Orthonormal bases exist in every Euclidean vector space. If there is an orthonormal basis, the vector can be represented in this basis:
- .
The coefficients are obtained by
- .
Isometrics
If and are two- dimensional Euclidean vector spaces, a linear mapping is called a (linear) isometry if it contains the scalar product, i.e. if
applies to all . Such a mapping is also called an orthogonal mapping . An isometry is given lengths in particular
and angles, especially orthogonality
Conversely, any linear mapping that receives lengths is an isometry.
An isometry maps each orthonormal basis back to an orthonormal basis. Conversely, if an orthonormal basis of and an orthonormal basis of , then there exists an isometric view, which on maps.
This means that two Euclidean vector spaces of the same dimension are isometric, that is, they cannot be distinguished as Euclidean vector spaces.
The Euclidean point space
motivation
Euclidean vector spaces often serve as models for Euclidean space. The elements of the vector space are then referred to as points or vectors, depending on the context. No distinction is made between points and their position vectors. This can be computationally advantageous. Conceptually, however, it is unsatisfactory:
- From a geometric point of view, points and vectors should be conceptually differentiated.
- Vectors can be added and multiplied by numbers, but points cannot.
- Points are connected by vectors or merged into one another.
- There is an excellent element in vector space , the zero vector . In Euclidean geometry, however, all points are equal.
description
The concept of the Euclidean point space provides a remedy . This is an affine space over a Euclidean vector space. A distinction is made here between points and vectors.
- The totality of the points forms the Euclidean point space. This is usually with , , or , respectively. (The superscript is not an exponent, but an index that characterizes the dimension. So it is not a Cartesian product.)
- The totality of all vectors forms a Euclidean vector space .
- For every two points and there is exactly one connection vector, which is designated with. The connection vector of a point with itself is the zero vector:
- A point can be converted into a point in an unambiguous manner by a vector . This is often referred to as. (This is a purely formal notation. The plus sign does not denote any vector space addition, and also no addition on the point space.) The zero vector leads every vector into itself:
- If the vector leads the point into the point and the vector leads the point into the point , then the point leads into the point . This can be expressed as follows:
In the language of algebra these properties mean: The additive group of the vector space operates freely and transitively on the set .
Lengths, distances and angles
Line lengths, distances between points, angles and orthogonality can now be defined with the help of the scalar product of vectors:
The length of the line and the distance between the points and is defined as the length of the vector :
The size of the angle is defined as the angle between the vectors and :
Two lines and are orthogonal if and only if the associated vectors and are orthogonal.
Illustrations
Length-preserving representations of a Euclidean point space are called isometries , congruence maps (in plane geometry) or movements . You will automatically get angles too. If there is a movement, there is an orthogonal mapping (linear isometry) , so that for all points and :
The real coordinate space
definition
The -dimensional real coordinate space is the -fold Cartesian product of the set of real numbers, i.e. the set of -Tuples where the real numbers are. Depending on the context , the elements of the are called points or vectors, so no distinction is made between points and vectors.
As vectors, they are added component by component and multiplied by real numbers:
In this case, the elements of the often (ie.. As column vectors - matrices ) wrote:
The scalar product ( standard scalar product ) is defined by
- .
With this scalar product it is a Euclidean vector space.
From Euclidean vector space / point space to coordinate space
If one chooses an orthonormal basis in a Euclidean vector space or a Cartesian coordinate system in a Euclidean point space (i.e. a coordinate origin and an orthonormal basis of the vector space), a coordinate tuple is thereby assigned to each vector or point . In this way an isometry is obtained between the given Euclidean space and the coordinate space and these can be identified with one another by means of this isometry. This justifies that as the designate Euclidean space. However, isometry depends on the choice of the orthonormal basis and - in the case of point space - on the choice of the origin.
Length, angle, orthogonality, standard base and spacing
As in every Euclidean vector space, the length or norm of a vector is given by the square root of the scalar product with itself:
This norm is also called Euclidean norm or 2-norm and writes instead of also or .
The angle between two vectors and is then calculated through
Two vectors and are orthogonal if and only if
applies. The vectors of the standard base
are unit vectors and orthogonal in pairs, i.e. they form an orthonormal basis .
If one considers the elements of the as points, then the distance between the points and as the length of the connection vector is defined:
Isometrics
The vector space isometrics (linear isometries) are orthogonal maps represented by orthogonal matrices . Is a linear isometric drawing and is
the image of the -th standard basis vector ( ) can be represented with the aid of matrix multiplication as
- .
Every isometry ( movement ) of the point space can be expressed in the form
as a link between an orthogonal mapping and a parallel shift (translation) .
orientation
Every finite-dimensional real vector space can be provided with an orientation by choosing an ordered basis . While no orientation is marked for any Euclidean vector and point spaces, the coordinate space has a canonical orientation that is given by the standard basis: The ordered basis from the vectors is positively oriented.
An orderly basis
is positively oriented if and only if the determinant formed from it is positive:
If the physical space (assumed to be Euclidean) is identified with the coordinate space by introducing a Cartesian coordinate system, the coordinate axes are usually chosen so that they form a right system . The orientation of the physical space given by the right-hand rule then corresponds to the canonical orientation of the coordinate space .
Euclidean space in other areas of mathematics
Euclidean spaces in topology
The function that assigns each vector its length defined by the scalar product is a norm . One speaks of the norm induced by the scalar product or the scalar product norm ; some authors also call the norm the Euclidean norm . The norm induced by the standard scalar product is called the Euclidean norm or 2-norm and is a special case of the p norms . As a result of the induced norm, every Euclidean vector space becomes a normalized space and thus a classic example of a topological vector space . In particular, it is a Prehilbert space and, because it is also complete in the finite-dimensional space , a Banach space and thus also a Hilbert space .
The Euclidean distance function turns every Euclidean space into a metric space and thus in particular into a topological space .
Since all norms are equivalent on finite-dimensional vector spaces , the topology of Euclidean space does not actually depend on the Euclidean structure. Normalized vector spaces of the same finite dimension are therefore all homeomorphic to one another and thus homeomorphic to the . After the set of the invariance of the dimension of Luitzen EJ Brouwer Euclidean spaces of different dimension are not homeomorphic successive imaged.
As a topological space, Euclidean space is contiguous and contractible .
Euclidean spaces in differential topology
Manifolds are modeled over Euclidean spaces: A manifold is locally homeomorphic to the . Due to the differentiable structure, differentiable manifolds are locally diffeomorphic to the . In particular, Euclidean space is itself a differentiable manifold. For all dimensions except dimension four, a too homeomorphic differentiable manifold is also too diffeomorphic. The exceptions existing in four dimensions are called exotic 4-rooms .
Euclidean spaces in differential geometry
The (not dependent on the point) scalar product turns the Euclidean space into a Riemannian manifold . Conversely, in Riemannian geometry, every Riemannian manifold that is isometric to the vector space with the standard scalar product is called Euclidean space. For these Riemannian manifolds the curvature tensor vanishes , that is, the space is flat. Conversely, every flat Riemannian manifold is locally isometric to Euclidean space. However, it can also be an open subset of a or a manifold whose universal superposition is a subset of the . Two-dimensional examples for the latter case are a flat torus or a straight circular cylinder . On the other hand, every complete and simply connected flat Riemannian manifold is a Euclidean space.
literature
- Marcel Berger: Geometry I. From the French by M. Cole and S. Levy. University text. Springer-Verlag, Berlin 1987, ISBN 3-540-11658-3 .
- Marcel Berger: Geometry II. From the French by M. Cole and S. Levy. University text. Springer-Verlag, Berlin 1987, ISBN 3-540-17015-4 .

























































![[PQ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/1103707481b5a55fd636cb13fdd707c6822b80c6)




![[RS]](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c7bd107332a0ad8203392dc1b896bc31b5c4655)




































