p norm

Unit circles of different p norms in two dimensions

In mathematics , the p -norms are a class of vector norms that are defined for real numbers . Important special cases are the sum norm , the Euclidean norm and as a limit value for the maximum norm . All norms are equivalent to each other , monotonically decreasing for increasing and satisfy the Minkowski inequality as well as the Hölder inequality . The sets of constant -norm ( unit spheres ) generally have the form of superellipsoids or subellipsoids. The norms form the basic building block for norms of further mathematical objects , such as sequences , functions , matrices and operators . ${\displaystyle p\geq 1}$ ${\displaystyle (p=1)}$ ${\displaystyle (p=2)}$ ${\displaystyle p\rightarrow \infty }$ ${\displaystyle p}$ ${\displaystyle p}$ ${\displaystyle p}$ ${\displaystyle p}$

definition

The norm of a real or complex vector with or is for real by ${\displaystyle p}$ ${\displaystyle x=(x_{1},\ldots ,x_{n})\in {\mathbb {K} }^{n}}$ ${\displaystyle {\mathbb {K} }=\mathbb {R} }$ ${\displaystyle {\mathbb {K} }=\mathbb {C} }$ ${\displaystyle 1\leq p<\infty }$

${\displaystyle \|x\|_{p}:=\left(\sum _{i=1}^{n}|x_{i}|^{p}\right)^{1/p}}$

defined, where is the amount of the component . It is irrelevant for the definition whether it is a row or a column vector . In this case , all norms correspond to the norm of the absolute value of a real or complex number. ${\displaystyle |x_{i}|}$ ${\displaystyle x_{i}}$ ${\displaystyle x}$ ${\displaystyle n=1}$ ${\displaystyle p}$

The set of vectors with -norm one is called the unit sphere of the norm, whereby only in this case the unit sphere actually corresponds to the sphere known from geometry . The unit spheres of norms are generally in two dimensions in the form of Super ellipses or Subellipsen and in three and higher dimensions the form of Superellipsoiden or Subellipsoiden. ${\displaystyle p}$ ${\displaystyle p=2}$ ${\displaystyle p}$ ${\displaystyle (2<p<\infty )}$ ${\displaystyle (1<p<2)}$

Important special cases

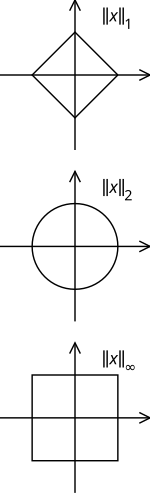
The unit circles of the sum norm, the Euclidean norm and the maximum norm in two dimensions

Sum norm

→ Main article : Sum norm

The 1 norm is also called sum norm or sum norm for short and is through

${\displaystyle \|x\|_{1}=\sum _{i=1}^{n}|x_{i}|}$

Are defined. It corresponds to the sum of the amounts of the components of the vector. The unit sphere of the real sum norm has the shape of a square in two dimensions, the shape of an octahedron in three dimensions and the shape of a cross polytope in general dimensions .

Euclidean norm

→ Main article : Euclidean norm

The 2 norm is the Euclidean norm and through

${\displaystyle \|x\|_{2}={\sqrt {\sum _{i=1}^{n}|x_{i}|^{2}}}}$

Are defined. It corresponds to the root of the sum of the squares of the absolute values ​​of the components of the vector. The unit sphere of the real Euclidean norm in two dimensions has the shape of a circle , in three dimensions the shape of a spherical surface and in general dimensions the shape of a sphere . The Euclidean norm describes the illustrative length of a vector in a plane or in space in two and three dimensions .

Maximum norm

→ Main article : Maximum norm

The ∞ norm (infinite norm) is obtained for the limit value , which is often also counted among the norms. It is also called the maximum norm or Chebyshev norm and is through ${\displaystyle p\rightarrow \infty }$ ${\displaystyle p}$

${\displaystyle \|x\|_{\infty }=\max _{i=1,\ldots ,n}|x_{i}|}$

Are defined. It therefore corresponds to the amount of the largest component of the vector. The unit sphere of the real maximum norm has the shape of a square in two dimensions, the shape of a cube in three dimensions and the shape of a hypercube in general dimensions .

That the maximum norm actually arises as a limit value of the norms for follows for from ${\displaystyle p}$ ${\displaystyle p\rightarrow \infty }$ ${\displaystyle x\neq 0}$

${\displaystyle \lim _{p\rightarrow \infty }\|x\|_{p}=\lim _{p\rightarrow \infty }\left(\sum _{i=1}^{n}|x_{i}|^{p}\right)^{1/p}\!\!\!\!\!=\|x\|_{\infty }\cdot \lim _{p\rightarrow \infty }\left(\sum _{i=1}^{n}\left({\frac {|x_{i}|}{\|x\|_{\infty }}}\right)^{p}\right)^{1/p}\!\!\!\!\!=\|x\|_{\infty }\cdot \lim _{p\rightarrow \infty }S^{1/p}=\|x\|_{\infty }}$,

since applies to the sum and thus the limit of for is equal to one. The lower bound of is assumed for a vector whose components are all but one equal to zero, and the upper bound for a vector whose components all have the same amount. By omitting the limit, it can be seen that the maximum norm is never greater than the other norms. ${\displaystyle 1\leq S\leq n}$ ${\displaystyle {\sqrt[{p}]{S}}}$ ${\displaystyle p\rightarrow \infty }$ ${\displaystyle S}$ ${\displaystyle n}$ ${\displaystyle p}$

Examples

Real vector

The 1, 2, 3, and ∞ norms of the real vector are each given as ${\displaystyle x=(3,-2,6)}$

${\displaystyle {\begin{aligned}\|x\|_{1}\,\,&=|3|+|{-2}|+|6|=11\\\|x\|_{2}\,\,&={\sqrt {|3|^{2}+|{-2}|^{2}+|6|^{2}}}={\sqrt {49}}=7\\\|x\|_{3}\,\,&={\sqrt[{3}]{|3|^{3}+|{-2}|^{3}+|6|^{3}}}={\sqrt[{3}]{251}}\approx 6{,}308\\\|x\|_{\infty }&=\max\{|3|,|{-2}|,|6|\}=6\end{aligned}}}$

Complex vector

The 1, 2, 3 and ∞ norms of the complex vector are each given as ${\displaystyle x=(3-4i,{-2i})}$

${\displaystyle {\begin{aligned}\|x\|_{1}\,\,&=|3-4i|+|{-2i}|=5+2=7\\\|x\|_{2}\,\,&={\sqrt {|3-4i|^{2}+|{-2i}|^{2}}}={\sqrt {5^{2}+2^{2}}}={\sqrt {29}}\approx 5{,}385\\\|x\|_{3}\,\,&={\sqrt[{3}]{|3-4i|^{3}+|{-2i}|^{3}}}={\sqrt[{3}]{5^{3}+2^{3}}}={\sqrt[{3}]{133}}\approx 5{,}104\\\|x\|_{\infty }&=\max\{|3-4i|,|{-2i}|\}=\max\{5,2\}=5\end{aligned}}}$

properties

Norm axioms

All norms including the maximum norm fulfill the three norm axioms definiteness , absolute homogeneity and subadditivity . The definiteness follows from the positivity of the power functions for positive arguments and the uniqueness of the zero at the point with which ${\displaystyle p}$ ${\displaystyle 0}$

${\displaystyle \|x\|_{p}=0\;\Leftrightarrow \;\left(\sum _{i=1}^{n}|x_{i}|^{p}\right)^{1/p}\!\!\!\!\!=0\;\Rightarrow \;\sum _{i=1}^{n}|x_{i}|^{p}=0\;\Rightarrow \;x=(0,\ldots ,0)=0}$

applies. The homogeneity follows from the homogeneity of the amount standard on

${\displaystyle \|\alpha \,x\|_{p}=\left(\sum _{i=1}^{n}|\alpha \,x_{i}|^{p}\right)^{1/p}\!\!\!\!\!=\left(\sum _{i=1}^{n}|\alpha |^{p}\,|x_{i}|^{p}\right)^{1/p}\!\!\!\!\!=|\alpha |\,\left(\sum _{i=1}^{n}|x_{i}|^{p}\right)^{1/p}\!\!\!\!\!=|\alpha |\,\|x\|_{p}}$.

The triangle inequality for norms is precisely the Minkowski inequality ${\displaystyle p}$

${\displaystyle \|x+y\|_{p}\leq \|x\|_{p}+\|y\|_{p}}$,

which in turn is based on the following Hölder inequality .

Holder's inequality

→ Main article : Hölder inequality

If exponents are conjugate to one another, that is, by convention , then the corresponding -norms apply ${\displaystyle 1\leq p,q\leq \infty }$ ${\displaystyle {\tfrac {1}{p}}+{\tfrac {1}{q}}=1}$ ${\displaystyle {\tfrac {1}{\infty }}=0}$ ${\displaystyle p}$

${\displaystyle \sum _{i=1}^{n}|x_{i}\,y_{i}|\leq \|x\|_{p}\cdot \|y\|_{q}}$,

which in turn follows from Young's inequality . In this case , the Hölder inequality corresponds to the Cauchy-Schwarz inequality . ${\displaystyle p=q=2}$

monotony

The norms are monotonically decreasing for a fixed vector and monotonically decreasing for increasing ones , that is, for applies ${\displaystyle p}$ ${\displaystyle x}$ ${\displaystyle p}$ ${\displaystyle 1\leq p<r\leq \infty }$

${\displaystyle \|x\|_{r}\leq \|x\|_{p}}$.

This property follows for and from the monotony of the power functions for through ${\displaystyle r<\infty }$ ${\displaystyle x\neq 0}$ ${\displaystyle z^{r}\leq z^{p}}$ ${\displaystyle z\in [0,1]}$

${\displaystyle \|x\|_{r}=\left(\sum _{i=1}^{n}|x_{i}|^{r}\right)^{1/r}\!\!\!\!\!=\|x\|_{p}\left(\sum _{i=1}^{n}\left({\frac {|x_{i}|}{\|x\|_{p}}}\right)^{r}\right)^{1/r}\!\!\!\!\!\leq \|x\|_{p}\left(\sum _{i=1}^{n}\left({\frac {|x_{i}|}{\|x\|_{p}}}\right)^{p}\right)^{1/r}\!\!\!\!\!=\|x\|_{p}\left({\frac {\|x\|_{p}^{p}}{\|x\|_{p}^{p}}}\right)^{1/r}\!\!\!\!\!=\|x\|_{p}}$,

because the fraction can only have a value between zero and one. For a given vector the sum norm is the largest and the maximum norm the smallest norm (see also the examples above). Equality across all norms applies if and only if the vector has at most one component not equal to zero, for example the zero vector or the -th unit vector . It is synonymous with monotony that the uniform spheres of the norms contain each other for growing , that is, for applies ${\displaystyle x}$ ${\displaystyle p}$ ${\displaystyle p}$ ${\displaystyle i}$ ${\displaystyle p}$ ${\displaystyle p}$ ${\displaystyle p<r}$

${\displaystyle \{x\colon \|x\|_{p}\leq 1\}\subset \{x\colon \|x\|_{r}\leq 1\}}$.

equivalence

All norms are equivalent to each other , that is, to any pair of norms with there are two positive constants and , so for all ${\displaystyle p}$ ${\displaystyle p}$ ${\displaystyle \|\cdot \|_{p},\|\cdot \|_{r}}$ ${\displaystyle 1\leq p\leq r\leq \infty }$ ${\displaystyle c_{1}}$ ${\displaystyle c_{2}}$ ${\displaystyle x\in V}$

${\displaystyle c_{1}\|x\|_{r}\leq \|x\|_{p}\leq c_{2}\|x\|_{r}}$

applies. The lower constant is always equal to one due to the monotony. The upper constant depends on the selected norms and is assumed for a vector with components of the same magnitude ( e.g. the one vector ). Namely, the Hölder inequality results in the choice of the Hölder exponents and for ${\displaystyle c_{1}}$ ${\displaystyle c_{2}}$ ${\displaystyle p'={\tfrac {r}{p}}}$ ${\displaystyle q'={\tfrac {1}{1-p/r}}}$ ${\displaystyle p,r<\infty }$

${\displaystyle \|x\|_{p}=\left(\sum _{i=1}^{n}|x_{i}|^{p}\cdot 1\right)^{1/p}\!\!\!\!\leq \left(\!\left(\sum _{i=1}^{n}\left(|x_{i}|^{p}\right)^{r/p}\right)^{p/r}\!\!\!\!\cdot \left(\sum _{i=1}^{n}1^{1/(1-p/r)}\right)^{1-p/r}\right)^{1/p}\!\!\!\!\!\!=n^{{\frac {1}{p}}-{\frac {1}{r}}}\,\|x\|_{r}}$.

With the convention in the exponent, this estimate also remains valid for or . The equivalence constant of the standards is summarized again in the following table: ${\displaystyle {\tfrac {1}{\infty }}=0}$ ${\displaystyle p=\infty }$ ${\displaystyle r=\infty }$ ${\displaystyle c_{2}}$ ${\displaystyle p}$ ${\displaystyle p\leq r}$

	${\displaystyle 1}$-Standard	${\displaystyle r}$-Standard	${\displaystyle \infty }$-Standard
${\displaystyle 1}$-Standard	${\displaystyle 1}$	${\displaystyle n^{1-{\frac {1}{r}}}}$	${\displaystyle n}$
${\displaystyle p}$-Standard	${\displaystyle 1}$	${\displaystyle n^{{\frac {1}{p}}-{\frac {1}{r}}}}$	${\displaystyle n^{\frac {1}{p}}}$
${\displaystyle \infty }$-Standard	${\displaystyle 1}$	${\displaystyle 1}$	${\displaystyle 1}$

For example, the entry in the first row and second column is for as ${\displaystyle r=2}$

${\displaystyle \|x\|_{1}\leq n^{1-{\frac {1}{2}}}\cdot \|x\|_{2}={\sqrt {n}}\cdot \|x\|_{2}}$

to read. The norms therefore differ for a fixed vector by a maximum of the factor . The optimal constants in such norm estimates lead to the calculation of distances in the Minkowski compact . ${\displaystyle p}$ ${\displaystyle x}$ ${\displaystyle n}$

Absoluteness

All norms including the maximum norm are absolutely, that is, for all vectors applies ${\displaystyle p}$ ${\displaystyle x\in {\mathbb {K} }^{n}}$

${\displaystyle \|x\|_{p}=\||x|\|_{p}}$,

where represents the component-wise magnitude of a vector. ${\displaystyle |x|=(|x_{1}|,\ldots ,|x_{n}|)}$

Component-wise monotony

Because of the absoluteness, the norms for fixed are monotonically increasing with the magnitude of each component of a vector , that is, it holds ${\displaystyle p}$ ${\displaystyle p}$ ${\displaystyle 1\leq p\leq \infty }$ ${\displaystyle x\in {\mathbb {K} }^{n}}$

${\displaystyle \|x\|_{p}\leq \|y\|_{p}}$

for everyone with for . For even applies strict monotony ${\displaystyle x,y\in {\mathbb {K} }^{n}}$ ${\displaystyle |x_{i}|\leq |y_{i}|}$ ${\displaystyle i=1,\ldots ,n}$ ${\displaystyle 1\leq p<\infty }$

${\displaystyle \|x\|_{p}<\|y\|_{p}}$

for everyone with for and for at least one . ${\displaystyle x,y\in {\mathbb {K} }^{n}}$ ${\displaystyle |x_{i}|\leq |y_{i}|}$ ${\displaystyle i=1,\ldots ,n}$ ${\displaystyle |x_{k}|<|y_{k}|}$ ${\displaystyle k\in \{1,\ldots ,n\}}$

Generalizations

Case p <1

The unit circle of the (2/3) -norm, a quasi-norm, is an astroid in two dimensions .

The figure defined for ${\displaystyle 0<p<1}$

${\displaystyle \|x\|_{p}=\left(\sum _{i=1}^{n}|x_{i}|^{p}\right)^{1/p}}$

is not a norm, because the resulting unit sphere is no longer convex and the triangle inequality is violated. These maps are only quasinorms , where the triangle inequality is replaced by the weaker inequality for a real constant . ${\displaystyle \|x+y\|\leq k\cdot \left(\|x\|+\|y\|\right)}$ ${\displaystyle k>1}$

ℓ ^p norms

→ Main article : Sequence space

The norms are the generalization of the norms to sequence spaces , where only the finite sum is replaced by an infinite sum. The norm in an amount as th power summable sequence is then for given as ${\displaystyle \ell ^{p}}$ ${\displaystyle p}$ ${\displaystyle \ell ^{p}}$ ${\displaystyle p}$ ${\displaystyle (a_{n})_{n}\in {\mathbb {K} }^{\mathbb {N} }}$ ${\displaystyle 1\leq p<\infty }$

${\displaystyle \|(a_{n})\|_{\ell ^{p}}=\left(\sum _{n=1}^{\infty }|a_{n}|^{p}\right)^{1/p}}$.

For the limit value there is the space of limited consequences with the supremum norm . ${\displaystyle p\rightarrow \infty }$

L ^p norms

→ Main article : Lp space

Furthermore, the norms can be generalized to function spaces, which happens in two steps. First, the -norms of a -th power on a set of Lebesgue integrable functions are for as ${\displaystyle p}$ ${\displaystyle {\mathcal {L}}^{p}}$ ${\displaystyle p}$ ${\displaystyle \Omega }$ ${\displaystyle f\colon \Omega \rightarrow {\mathbb {K} }}$ ${\displaystyle 1\leq p<\infty }$

${\displaystyle \|f\|_{{\mathcal {L}}^{p}(\Omega )}=\left(\int _{\Omega }|f(x)|^{p}\,dx\right)^{1/p}}$,

defined, whereas in comparison to the norms only the sum was replaced by an integral. These norms are initially only semi-norms , since not only the null function , but also all functions that differ from the null function only in a set with Lebesgue measure zero, are integrated to zero. Therefore one considers here the set of equivalence classes of functions , which are almost everywhere the same, and obtains the norms in these spaces ${\displaystyle \ell ^{p}}$ ${\displaystyle [f]\in L^{p}(\Omega )}$ ${\displaystyle L^{p}}$ ${\displaystyle L^{p}}$

${\displaystyle \|\,[f]\,\|_{L^{p}(\Omega )}=\|f\|_{{\mathcal {L}}^{p}(\Omega )}}$.

For the limit value, this results in the space of the essentially restricted functions with the essential supreme norm . The norms and spaces can also be generalized from the Lebesgue measure to general measures and from real or complex-valued functions to Banach space-valued functions by replacing the absolute value with the corresponding norm. ${\displaystyle p\rightarrow \infty }$ ${\displaystyle L^{p}}$

Matrix norms

→ Main article : Matrix norm

By simply viewing a matrix as a correspondingly long vector , matrix norms can be defined directly via the norms. Examples of such matrix norms are the Frobenius norm based on the 2 norm and the overall norm based on the ∞ norm . Matrix norms, however, are mostly induced by a norm as an induced matrix norm ${\displaystyle A=(a_{ij})\in {\mathbb {K} }^{m\times n}}$ ${\displaystyle {\mathbb {K} }^{m\cdot n}}$ ${\displaystyle p}$ ${\displaystyle p}$

${\displaystyle \|A\|_{p}=\max _{x\neq 0}{\frac {\|Ax\|_{p}}{\|x\|_{p}}}=\max _{\|x\|_{p}=1}\|Ax\|_{p}}$.

derived. Examples of matrix norms defined in this way are the column total norm based on the 1 norm , the spectral norm based on the 2 norm and the row total norm based on the ∞ norm . Another possibility to define matrix norms is to consider the norm of the vector of the singular values ​​of the matrix, as is the case with the shadow norms . Norms for more general linear operators can also be defined in an analogous manner . ${\displaystyle p}$ ${\displaystyle p}$

literature

• Hans Wilhelm Alt: Linear Functional Analysis: An Application-Oriented Introduction . 5th edition. Springer-Verlag, 2008, ISBN 3-540-34186-2 .
• Gene Golub , Charles van Loan: Matrix Computations . 3. Edition. Johns Hopkins University Press, 1996, ISBN 978-0-8018-5414-9 .
• Roger Horn, Charles R. Johnson: Matrix Analysis . Cambridge University Press, 1990, ISBN 978-0-521-38632-6 .
• Hans Rudolf Schwarz, Norbert Köckler: Numerical Mathematics . 8th edition. Vieweg & Teubner, 2011, ISBN 978-3-8348-1551-4 .

Web links

• Eric W. Weisstein : Vector Norm . In: MathWorld (English).
• Andrea Ambrosio, Logan Hanks, Pedro Sanchez: Vector p-norm . In: PlanetMath . (English)

Individual evidence

1. ^ Friedrich L. Bauer , Josef Stoer , Christoph Witzgall: Absolute and monotonic norms . In: Numerical Mathematics . tape 3 , no. 1 , 1961, pp. 257-264 .
2. ↑ Matthias Ehrgott: Multicriteria Optimization . 2nd Edition. Springer, 2005, p. 111-113 .