Measure (mathematics)

A measure assigns subsets of a basic set of numbers. The picture illustrates the monotony property of measures, that is, larger quantities also have a larger measure.

In mathematics, a measure is a function that assigns suitable subsets of a basic set of numbers that can be interpreted as a “ measure ” for the size of these sets. Both the definition range of a measure, i.e. the measurable quantities, and the assignment itself must meet certain requirements, as suggested, for example, by elementary geometric concepts of the length of a line , the area of a geometric figure or the volume of a body.

The branch of mathematics that deals with the construction and study of dimensions is dimension theory . The general concept of dimension goes back to the work of Émile Borel , Henri Léon Lebesgue , Johann Radon and Maurice René Fréchet . Dimensions are always closely related to the integration of functions and form the basis of modern integral terms (see Lebesgue integral ). Since the axiomatization of probability theory by Andrei Kolmogorov is stochastics another large field of application for measurements. There are probability measures used to random events , as subsets of a sample space to assign probabilities to be construed.

Introduction and story

The elementary geometric surface area assigns numerical values ​​to flat geometric figures such as rectangles, triangles or circles, i.e. certain subsets of the Euclidean plane . Area contents can be equal to zero, for example for the empty set , but also for individual points or for routes. Also the "value" ( infinite ) comes z. B. for half-planes or the outside of circles as area. However, negative numbers must not appear as areas. ${\displaystyle \infty }$

Countable additivity of a measure : The measure of a countable disjoint union is equal to the sum over the measures of the individual subsets. ${\displaystyle \mu }$

Furthermore, the area of ​​planar geometric figures has a property called additivity : If a figure is broken down into two or more parts, for example a rectangle using a diagonal into two triangles, then the area of ​​the initial figure is the sum of the areas of the parts. “Decompose” here means that the parts have to be disjoint in pairs (i.e. no two parts have any points in common) and that the union of all parts results in the initial figure. For the measurement of areas of more complicated figures, such as circular areas or areas that are enclosed between function graphs (i.e. for the calculation of integrals), limit values of areas must be considered. For this it is important that the additivity still applies when surfaces are broken down into a sequence of pairwise disjoint partial surfaces. This property is called countable additivity or σ-additivity .

Henri Léon Lebesgue

The importance of σ-additivity for the concept of measure was first recognized by Émile Borel, who proved in 1894 that the elementary geometric length possesses this property. Henri Lebesgue formulated and investigated the actual measurement problem in his doctoral thesis in 1902: He constructed a σ-additive measure for subsets of the real numbers (the Lebesgue measure ), which continues the length of intervals, but not for all subsets, but for one System of subsets, which he called measurable quantities. In 1905 Giuseppe Vitali showed that a consistent extension of the concept of length to all subsets of real numbers is impossible, that is, that the measurement problem cannot be solved.

Since important measures such as the Lebesgue measure cannot be defined for all subsets (i.e. on the power set ) of the basic set, suitable domains of definition for measures must be considered. The σ-additivity suggests that systems of measurable sets should be closed with respect to countable set operations. This leads to the requirement that the measurable quantities must form a σ-algebra . That means: The basic set itself is measurable and complements as well as countable combinations of measurable sets can in turn be measured.

In the following years, Thomas Jean Stieltjes and Johann Radon expanded the construction of the Lebesgue measure to include more general measures in -dimensional space, the Lebesgue-Stieltjes measure . From 1915, Maurice René Fréchet also considered measures and integrals on arbitrary abstract sets. In 1933 Andrei Kolmogorow published his textbook Basic Concepts of Probability Theory , in which he used measure theory to give a strict axiomatic justification of probability theory (see also History of Probability Theory ). ${\displaystyle d}$

definition

Let be a σ-algebra over a non-empty basic set . A function is called measure if both of the following conditions are met: ${\displaystyle {\mathcal {A}}}$ ${\displaystyle \Omega }$ ${\displaystyle \mu \colon {\mathcal {A}}\to [0,\infty ]}$ ${\displaystyle {\mathcal {A}}}$

• ${\displaystyle \mu (\emptyset )=0}$
• σ-additivity : For every sequence of pairwise disjoint sets from holds . ${\displaystyle (A_{n})_{n\in \mathbb {N} }}$ ${\displaystyle {\mathcal {A}}}$ ${\displaystyle \mu \left(\bigcup _{n=1}^{\infty }A_{n}\right)=\sum _{n=1}^{\infty }\mu (A_{n})}$

If the σ-algebra is clear from the context, one also speaks of a measure ${\displaystyle \Omega }$ .

A subset of that lies in is called measurable . For such a person is called the measure of quantity . The triple is called the dimension space . The pair consisting of the basic set and the σ-algebra defined on it is called the measurement space or measurable space . A measure is thus one on a measurement space defined non-negative σ-additive set function with . ${\displaystyle \Omega }$ ${\displaystyle {\mathcal {A}}}$ ${\displaystyle A\in {\mathcal {A}}}$ ${\displaystyle \mu (A)}$ ${\displaystyle A}$ ${\displaystyle (\Omega ,{\mathcal {A}},\mu )}$ ${\displaystyle (\Omega ,{\mathcal {A}})}$ ${\displaystyle \mu }$ ${\displaystyle \mu (\emptyset )=0}$

The measure is called the probability measure (or standardized measure), if this also applies. A measure space with a probability measure is a probability space. If it is more general , it is called a finite measure . If there are countably many sets, the measure of which is finite and the union of which results in whole , then a σ-finite (or σ-finite) measure is called. ${\displaystyle \mu }$ ${\displaystyle \mu (\Omega )=1}$ ${\displaystyle (\Omega ,{\mathcal {A}},\mu )}$ ${\displaystyle \mu }$ ${\displaystyle \mu (\Omega )<\infty }$ ${\displaystyle \mu }$ ${\displaystyle \Omega }$ ${\displaystyle \mu }$

Notes and first examples

• So a measure takes non-negative values ​​from the extended real numbers . The usual conventions apply for calculating with , it is also useful to set. ${\displaystyle {\bar {\mathbb {R} }}}$ ${\displaystyle \infty }$ ${\displaystyle 0\cdot (\pm \infty ):=0}$
• Since all summands of the series are non-negative, this is either convergent or divergent to . ${\displaystyle \textstyle \sum _{n=1}^{\infty }\mu (A_{n})}$ ${\displaystyle +\infty }$
• The requirement that the empty set has the measure zero excludes the case that all have the measure . Indeed, the requirement can equivalently be replaced by the condition that one exists with . In contrast, the trivial cases are for all (the so-called zero measure) and for all (and ) measures in the sense of the definition. ${\displaystyle A\in {\mathcal {A}}}$ ${\displaystyle \mu (A)=\infty }$ ${\displaystyle \mu (\emptyset )=0}$ ${\displaystyle A\in {\mathcal {A}}}$ ${\displaystyle \mu (A)<\infty }$ ${\displaystyle \mu (A):=0}$ ${\displaystyle A\in {\mathcal {A}}}$ ${\displaystyle \mu (A):=\infty }$ ${\displaystyle A\in {\mathcal {A}}\setminus \{\emptyset \}}$ ${\displaystyle \mu (\emptyset ):=0}$
• For an element , ${\displaystyle x\in \Omega }$

${\displaystyle \delta _{x}(A):={\begin{cases}1\ ,&{\text{falls }}x\in A\ ,\\0\ ,&{\text{sonst}}\end{cases}}}$

defined for a measure. It is called the Dirac measure at the point and is a probability measure. ${\displaystyle A\in {\mathcal {A}}}$ ${\displaystyle x}$

• The mapping that assigns the number of its elements, i.e. their cardinality , to each finite set , as well as the infinite sets in the value , is called the count . The counting measure is a finite measure if it is a finite set, and a σ-finite measure if it is at most countable . ${\displaystyle \mu \colon {\mathcal {A}}\to [0,\infty ]}$ ${\displaystyle A\in {\mathcal {A}}}$ ${\displaystyle |A|}$ ${\displaystyle {\mathcal {A}}}$ ${\displaystyle \infty }$ ${\displaystyle \Omega }$ ${\displaystyle \Omega }$
• The -dimensional Lebesgue measure is a measure on the σ-algebra of the Lebesgue-measurable subsets of . It is clearly determined by the requirement that it assigns their volume to the -dimensional hyper-rectangles : ${\displaystyle d}$ ${\displaystyle \lambda }$ ${\displaystyle \mathbb {R} ^{d}}$ ${\displaystyle d}$

${\displaystyle \lambda ([a_{1},b_{1}]\times \dotsb \times [a_{d},b_{d}])=(b_{1}-a_{1})\dotsm (b_{d}-a_{d})}$.

The Lebesgue measure is not finite, but σ-finite.

• The Hausdorff measure is a generalization of the Lebesgue measure to dimensions that are not necessarily whole numbers. With its help, the Hausdorff dimension can be defined, a dimension term with which, for example, fractal quantities can be examined.

properties

Calculation rules

The following elementary calculation rules for a measure result directly from the definition : ${\displaystyle \mu \colon {\mathcal {A}}\to [0,\infty ]}$

• Finite additivity: For pairwise disjoint sets we have . ${\displaystyle A_{1},\dotsc ,A_{m}\in {\mathcal {A}}}$ ${\displaystyle \textstyle \mu (A_{1}\cup \ldots \cup A_{m})=\sum _{n=1}^{m}\mu (A_{n})}$
• Subtractivity: For with and applies . ${\displaystyle A,B\in {\mathcal {A}}}$ ${\displaystyle B\subseteq A}$ ${\displaystyle \mu (B)<\infty }$ ${\displaystyle \mu (A\setminus B)=\mu (A)-\mu (B)}$
• Monotony: applies to with . ${\displaystyle A,B\in {\mathcal {A}}}$ ${\displaystyle B\subseteq A}$ ${\displaystyle \mu (B)\leq \mu (A)}$
• For true always . With the principle of inclusion and exclusion , this formula can be generalized in the case of finite measures to unions and intersections of finitely many sets. ${\displaystyle A,B\in {\mathcal {A}}}$ ${\displaystyle \mu (A\cup B)+\mu (A\cap B)=\mu (A)+\mu (B)}$
• σ-subadditivity : For any sequence of sets in is true . ${\displaystyle (A_{n})_{n\in \mathbb {N} }}$ ${\displaystyle {\mathcal {A}}}$ ${\displaystyle \textstyle \mu \left(\bigcup _{n=1}^{\infty }A_{n}\right)\leq \sum _{n=1}^{\infty }\mu (A_{n})}$

Continuity properties

The following continuity properties are fundamental for approximating measurable sets. They follow directly from the σ-additivity.

• σ-continuity from below : If there is an increasing sequence of sets consisting of and , then we have . ${\displaystyle A_{1}\subseteq A_{2}\subseteq \dotsb }$ ${\displaystyle {\mathcal {A}}}$ ${\displaystyle A=\bigcup _{n=1}^{\infty }A_{n}}$ ${\displaystyle \lim _{n\to \infty }\mu (A_{n})=\mu (A)}$
• σ-continuity from above : If there is a descending sequence of sets with and , then we have . ${\displaystyle A_{1}\supseteq A_{2}\supseteq \dotsb }$ ${\displaystyle {\mathcal {A}}}$ ${\displaystyle \mu (A_{1})<\infty }$ ${\displaystyle A=\bigcap _{n=1}^{\infty }A_{n}}$ ${\displaystyle \lim _{n\to \infty }\mu (A_{n})=\mu (A)}$

Uniqueness set

→ Main article : Measure uniqueness theorem

The following uniqueness principle applies to two dimensions in a common measuring space : ${\displaystyle \mu ,\nu \colon {\mathcal {A}}\to [0,\infty ]}$ ${\displaystyle (\Omega ,{\mathcal {A}})}$

There is an average stable producer of , i. H. it applies and for all is , with the following characteristics: ${\displaystyle {\mathcal {E}}}$ ${\displaystyle {\mathcal {A}}}$ ${\displaystyle {\mathcal {A}}=\sigma ({\mathcal {E}})}$ ${\displaystyle E_{1},E_{2}\in {\mathcal {E}}}$ ${\displaystyle E_{1}\cap E_{2}\in {\mathcal {E}}}$

1. So , and applies to everyone ${\displaystyle E\in {\mathcal {E}}}$ ${\displaystyle \mu (E)=\nu (E)}$ ${\displaystyle \mu |_{\mathcal {E}}=\nu |_{\mathcal {E}}}$
2. There is a sequence of sets in with and for everyone . ${\displaystyle (E_{n})_{n\in \mathbb {N} }}$ ${\displaystyle {\mathcal {E}}}$ ${\displaystyle \bigcup _{n=1}^{\infty }E_{n}=\Omega }$ ${\displaystyle \mu (E_{n})=\nu (E_{n})<\infty }$ ${\displaystyle n\in \mathbb {N} }$

Then applies . ${\displaystyle \mu =\nu }$

For finite measures with , condition 2 is automatically fulfilled. In particular, two probability measures are equal if they agree on a stable average generator of the event algebra. ${\displaystyle \mu (\Omega )=\nu (\Omega )}$

The uniqueness theorem provides, for example, the uniqueness of the continuation of a premeasure to a measure by means of an external measure and the measure extension theorem from Carathéodory .

Linear combinations of dimensions

Poisson distributions - shown here for the parameter values (blue), (green) and (red) - are measures on . They can be constructed as convex combinations of Dirac dimensions. ${\displaystyle \lambda =1}$ ${\displaystyle \lambda =5}$ ${\displaystyle \lambda =10}$ ${\displaystyle \mathbb {N} _{0}}$

For a family of measures on the same measurement space and for non-negative real constants , a measure is again defined by. In particular, sums and non-negative multiples of measures are also measures. ${\displaystyle (\mu _{i})_{i\in I}}$ ${\displaystyle (\alpha _{i})_{i\in I}}$ ${\displaystyle \textstyle \mu =\sum _{i\in I}\alpha _{i}\mu _{i}}$

If, for example, is a countable basic set and , then with the Dirac measures there is a measure on the power set of . Conversely, one can show that in this way, given a countable basic set, one obtains all measures on the power set. ${\displaystyle \Omega =(\omega _{i})_{i\in \mathbb {N} }}$ ${\displaystyle \alpha _{i}\geq 0}$ ${\displaystyle \textstyle \mu :=\sum _{i\in \mathbb {N} }\alpha _{i}\delta _{x_{i}}}$ ${\displaystyle \delta _{x_{i}}}$ ${\displaystyle \Omega }$

If probability measures are on and non-negative real numbers with , then the convex combination is again a probability measure. By convex combination of Dirac measures one obtains discrete probability distributions , in general mixed distributions result . ${\displaystyle (\mu _{i})_{i\in \mathbb {N} }}$ ${\displaystyle (\Omega ,{\mathcal {A}})}$ ${\displaystyle (\alpha _{i})_{i\in \mathbb {N} }}$ ${\displaystyle \textstyle \sum _{i\in \mathbb {N} }\alpha _{i}=1}$ ${\displaystyle \textstyle \mu :=\sum _{i\in \mathbb {N} }\alpha _{i}\mu _{i}}$

Construction of dimensions

Dimension extension set

Constantin Carathéodory

Since the elements of σ-algebras, such as in the Borel σ-algebra on , often can not be explicitly specified are frequently extent by continuing constructed by lot of features. The most important tool for this is the Carathéodory extension set . It says that every non-negative σ-additive set function on a set ring (a so-called premeasure ) can be continued to a measure on the σ-algebra generated by . The continuation is unambiguous if the premeasure is σ-finite. ${\displaystyle \mathbb {R} ^{d}}$ ${\displaystyle {\mathcal {R}}}$ ${\displaystyle {\mathcal {R}}}$

For example, all subsets of which can be represented as a finite union of axially parallel -dimensional intervals form a set ring. The elementary volume content of these so-called figures, the Jordan content , is a premeasure on this volume ring. The σ-algebra generated by the figures is the Borel σ-algebra and the continuation of the Jordan content according to Carathéodory results in the Lebesgue-Borel measure. ${\displaystyle \mathbb {R} ^{d}}$ ${\displaystyle d}$

Zero quantities, completion of measurements

→ Main articles : Zero Quantity  and Complete Measure Space

Is a measure and a quantity with , then is called zero quantity . It is obvious to assign the measure zero to subsets of a zero set. However, such quantities do not necessarily have to be measurable, i.e. lie in again . A measurement space in which subsets of zero quantities can always be measured is called complete. For a dimension space that is not complete, a complete dimension space - called the completion - can be constructed. For example, the completion of the Lebesgue-Borel measure is the Lebesgue measure on the Lebesgue-measurable subsets of the . ${\displaystyle \mu }$ ${\displaystyle A\in {\mathcal {A}}}$ ${\displaystyle \mu (A)=0}$ ${\displaystyle A}$ ${\displaystyle {\mathcal {A}}}$ ${\displaystyle \mathbb {R} ^{d}}$

Measures on the real numbers

The Lebesgue measure on is characterized by the fact that it assigns length to intervals . Its construction can be generalized with the help of a monotonically increasing function to the Lebesgue-Stieltjes measures , which assign the “weighted length” to the intervals . If the function is also continuous on the right-hand side , this defines a premeasure on the set ring of the finite associations of such intervals. According to Carathéodory, this can be extended to a degree on the Borel quantities of or to its completion. For example, the Lebesgue measure results again for the identical mapping ; if, on the other hand, a step function that is constant piecewise, one obtains linear combinations of Dirac measures. ${\displaystyle \lambda }$ ${\displaystyle \mathbb {R} }$ ${\displaystyle (a,b]\subseteq \mathbb {R} }$ ${\displaystyle b-a}$ ${\displaystyle F\colon \mathbb {R} \to \mathbb {R} }$ ${\displaystyle \lambda _{F}}$ ${\displaystyle (a,b]}$ ${\displaystyle F(b)-F(a)}$ ${\displaystyle F}$ ${\displaystyle \mathbb {R} }$ ${\displaystyle F(x)=x}$ ${\displaystyle F}$

The Cantor function (shown here with 10 iterations) is the distribution function of a probability measure , the Cantor distribution. ${\displaystyle \mathbb {R} }$

If a function that is continuous and monotonically increasing on the right side , the conditions are also added ${\displaystyle F\colon \mathbb {R} \to \mathbb {R} }$

${\displaystyle \lim \limits _{x\to -\infty }F(x)=0}$  and   ${\displaystyle \lim \limits _{x\to +\infty }F(x)=1}$

is fulfilled, the Lebesgue-Stieltjes measure constructed in this way is a probability measure. Its distribution function is the same , that means . Conversely, every distribution function has a probability measure on the above properties. With the help of distribution functions, it is possible to simply represent such probability measures that are neither discrete nor have a Lebesgue density, such as the Cantor distribution . ${\displaystyle \lambda _{F}}$ ${\displaystyle F}$ ${\displaystyle F(x)=\lambda _{F}((-\infty ,x])}$ ${\displaystyle F}$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {R} }$

Limitation of dimensions

As each function a measure can be of course on a smaller domain, so a σ-algebra limit . For example, by restricting the Lebesgue measure to the Borel σ-algebra, the Lebesgue-Borel measure is restored. ${\displaystyle \mu \colon {\mathcal {A}}\to [0,\infty ]}$ ${\displaystyle {\mathcal {B}}\subseteq {\mathcal {A}}}$

It is more interesting to restrict it to a smaller basic set : If a measure space is and , then becomes through ${\displaystyle X\subseteq \Omega }$ ${\displaystyle (\Omega ,{\mathcal {A}},\mu )}$ ${\displaystyle X\in {\mathcal {A}}}$

${\displaystyle {\mathcal {A}}|_{X}:=\{A\cap X\mid A\in {\mathcal {A}}\}}$

defines a σ-algebra , the so-called trace σ-algebra . It applies exactly when and is. For this is through ${\displaystyle X}$ ${\displaystyle A\in {\mathcal {A}}|_{X}}$ ${\displaystyle A\in {\mathcal {A}}}$ ${\displaystyle A\subseteq X}$ ${\displaystyle A}$

${\displaystyle \mu |_{X}(A):=\mu (A)}$

defines a measure of up called the restriction (or trace) of up . For example, by restricting the Lebesgue measure from to the interval because of a probability measure , the constant uniform distribution . ${\displaystyle {\mathcal {A}}|_{X}}$ ${\displaystyle \mu }$ ${\displaystyle X}$ ${\displaystyle \lambda }$ ${\displaystyle \mathbb {R} }$ ${\displaystyle [0,1]}$ ${\displaystyle \lambda ([0,1])=1}$ ${\displaystyle [0,1]}$

Image dimension

→ Main article : Image dimension

Dimensions can be transformed from one measurement space to another measurement space with the help of measurable functions . Are and measuring rooms, it means a function measurable if for all the archetype in lies. Is now a measure on , then the function with for a degree . It is called the image dimension of under and is often referred to as or . ${\displaystyle (\Omega ,{\mathcal {A}})}$ ${\displaystyle (\Omega ',{\mathcal {A}}')}$ ${\displaystyle T\colon \Omega \to \Omega '}$ ${\displaystyle A'\in {\mathcal {A}}'}$ ${\displaystyle T^{-1}(A')}$ ${\displaystyle {\mathcal {A}}}$ ${\displaystyle \mu }$ ${\displaystyle {\mathcal {A}}}$ ${\displaystyle \mu '\colon {\mathcal {A}}'\to [0,\infty ]}$ ${\displaystyle \mu '(A'):=\mu (T^{-1}(A'))}$ ${\displaystyle A'\in {\mathcal {A}}'}$ ${\displaystyle {\mathcal {A}}'}$ ${\displaystyle \mu }$ ${\displaystyle T}$ ${\displaystyle \mu _{T}}$ ${\displaystyle \mu \circ T^{-1}}$

The behavior of integrals when transforming measures is described by the transformation theorem . By means of image measures it is possible in analysis to construct measures on manifolds .

Image measures of probability measures are again probability measures. This fact plays an important role when considering the probability distributions of random variables in stochastics.

Dimensions with densities

The standard normal distribution is a measure on the real numbers that can be specified using its Lebesgue density.

Measures are often constructed as "indefinite integrals" of functions with respect to other measures. Is a measure space and a non-negative measurable function, then through ${\displaystyle (\Omega ,{\mathcal {A}},\mu )}$ ${\displaystyle f\colon \Omega \to [0,\infty ]}$

${\displaystyle \nu (A)=\int _{A}f\,\mathrm {d} \mu }$

for another degree on defined. The function is called the density function of with respect to (short a density). A common notation is . ${\displaystyle A\in {\mathcal {A}}}$ ${\displaystyle (\Omega ,{\mathcal {A}})}$ ${\displaystyle f}$ ${\displaystyle \nu }$ ${\displaystyle \mu }$ ${\displaystyle \mu }$ ${\displaystyle f={\tfrac {\mathrm {d} \nu }{\mathrm {d} \mu }}}$

The Radon-Nikodym theorem provides information about which dimensions can be represented by means of densities: Is σ-finite, then this is just possible if all zero amounts of even zero amounts of are. ${\displaystyle \mu }$ ${\displaystyle \mu }$ ${\displaystyle \nu }$

In stochastics, the distributions of continuous random variables , such as the normal distribution , are often given by densities with respect to the Lebesgue measure.

Product dimensions

→ Main article : Product dimension

If a basic quantity can be written as a Cartesian product and if dimensions are given for the individual factors, a so-called product dimension can be constructed on it. For two measure spaces and denote the product σ-algebra . This is the smallest σ-algebra that contains all set products with and . If and are σ-finite, then there is exactly one measure for with ${\displaystyle (\Omega _{1},{\mathcal {A}}_{1},\mu _{1})}$ ${\displaystyle (\Omega _{2},{\mathcal {A}}_{2},\mu _{2})}$ ${\displaystyle {\mathcal {A}}:={\mathcal {A}}_{1}\otimes {\mathcal {A}}_{2}}$ ${\displaystyle \Omega :=\Omega _{1}\times \Omega _{2}}$ ${\displaystyle A_{1}\times A_{2}}$ ${\displaystyle A_{1}\in {\mathcal {A}}_{1}}$ ${\displaystyle A_{2}\in {\mathcal {A}}_{2}}$ ${\displaystyle \mu _{1}}$ ${\displaystyle \mu _{2}}$ ${\displaystyle \mu }$ ${\displaystyle (\Omega ,{\mathcal {A}})}$

${\displaystyle \mu (A_{1}\times A_{2})=\mu _{1}(A_{1})\cdot \mu _{2}(A_{2})}$,

the product dimension is named and denoted by. Products of finitely many dimensions can also be formed in a completely analogous manner. For example, the Lebesgue-Borel measure on the -dimensional Euclidean space is obtained as a -fold product of the Lebesgue-Borel measure on the real numbers. ${\displaystyle \mu _{1}\otimes \mu _{2}}$ ${\displaystyle d}$ ${\displaystyle \mathbb {R} ^{d}}$ ${\displaystyle d}$

With the help of Fubini's theorem , integrals with regard to a product dimension can usually be calculated by performing step-by-step integrations with regard to the individual dimensions . In this way, for example, area and volume calculations can be traced back to the determination of one-dimensional integrals. ${\displaystyle \mu _{1}\otimes \dotsb \otimes \mu _{d}}$ ${\displaystyle \mu _{i}}$

In contrast to general measures, any (even uncountable) products can be formed under certain conditions with probability measures. For example, products of probability spaces model the independent repetition of random experiments.

Dimensions on topological spaces

If the basic set is also a topological space , one is primarily interested in measures that have similar properties to the Lebesgue measure or the Lebesgue-Stieltjes measure in the topological space with the standard topology. A simple consideration shows that Borel's σ-algebra is generated not only from the set of -dimensional intervals, but also from the open subsets . If, therefore, a Hausdorff space with topology (i.e. the set of open sets), then the Borel σ-algebra is defined as ${\displaystyle \Omega }$ ${\displaystyle \mathbb {R} ^{d}}$ ${\displaystyle \mathbb {R} ^{d}}$ ${\displaystyle d}$ ${\displaystyle (\Omega ,{\mathfrak {T}})}$ ${\displaystyle {\mathfrak {T}}}$ ${\displaystyle \Omega }$

${\displaystyle {\mathcal {B}}:={\mathcal {B}}(\Omega ):=\sigma ({\mathfrak {T}})}$,

thus as the smallest σ-algebra that contains all open sets. Of course, it then also contains all closed sets as well as all sets that can be written as countable unions or averages of closed or open sets (cf. Borel hierarchy ). ${\displaystyle {\mathcal {B}}}$

Borel measures and regularity

→ Main articles : Borel measure  and regular measure

A measure in a measuring space , Hausdorff space and the Borel σ-algebra, is called Borel measure if it is locally finite. That is, each has an open environment , the measure of which is finite. If additionally locally compact , it is equivalent to the fact that all compact sets have finite measure. ${\displaystyle \mu \colon {\mathcal {B}}\to [0,\infty ]}$ ${\displaystyle (\Omega ,{\mathcal {B}})}$ ${\displaystyle \Omega }$ ${\displaystyle {\mathcal {B}}}$ ${\displaystyle \omega \in \Omega }$ ${\displaystyle \Omega }$

A Radon measure is a Borel measure, which is regularly from the inside, this means that for each applicable ${\displaystyle A\in {\mathcal {B}}}$

${\displaystyle \mu (A)=\sup\{\mu (K)\mid K\subset A,\ K\ {\text{kompakt}}\}}$.

Is a Radon measure in addition regularly from the outside, that is, for each applicable ${\displaystyle A\in {\mathcal {B}}}$

${\displaystyle \mu (A)=\inf\{\mu (U)\mid A\subset U,\ U\ {\text{offen}}\}}$,

so it is called the regular Borel measure.

Numerous important Borel measures are regular, namely the following statements on regularity apply:

• If a locally compact Hausdorff space with a countable basis (second countability axiom ), then every Borel measure is regular. ${\displaystyle \Omega }$ ${\displaystyle \Omega }$
• Every Borel measure in a Polish area is regular.

Probability measures on Polish spaces play an important role in numerous existential questions in probability theory.

Hairy measure

→ Main article : Haarsches Maß

The -dimensional Euclidean space is not only a locally compact topological space, but even a topological group with regard to the usual vector addition as a link. The Lebesgue measure also respects this structure in the sense that it is invariant to translations: applies to all Borel sets and all ${\displaystyle d}$ ${\displaystyle \lambda }$ ${\displaystyle A}$ ${\displaystyle x\in \mathbb {R} ^{d}}$

${\displaystyle \lambda (A+x)=\lambda (A)}$.

The concept of the Haar measure generalizes this translation invariance to left-invariant Radon measures on Hausdorff locally compact topological groups . Such a measure always exists and is uniquely determined except for a constant factor. The Haar measure is finite if and only if the group is compact; in this case it can be normalized to a probability measure.

Haar's measures play a central role in harmonic analysis , in which methods of Fourier analysis are applied to general groups.

Convergence of dimensions

The most important concept of convergence for sequences of finite measures is weak convergence , which can be defined with the help of integrals as follows:
Let it be a metric space . A sequence of finite measures on is called weakly convergent to a finite measure , in signs , if it holds for all bounded continuous functions ${\displaystyle \Omega }$ ${\displaystyle (\mu _{n})_{n\in \mathbb {N} }}$ ${\displaystyle (\Omega ,{\mathcal {B}}(\Omega ))}$ ${\displaystyle \mu \colon {\mathcal {B}}(\Omega )\to [0,\infty )}$ ${\displaystyle \mu _{n}{\xrightarrow {w}}\mu }$ ${\displaystyle f\colon \Omega \to \mathbb {R} }$

${\displaystyle \lim _{n\to \infty }\int _{\Omega }f\,\mathrm {d} \mu _{n}=\int _{\Omega }f\,\mathrm {d} \mu }$.

The convergence of measures indicates some other conditions that are equivalent to the weak convergence of measures. For example, if and only if ${\displaystyle \mu _{n}{\xrightarrow {w}}\mu }$

${\displaystyle \lim _{n\to \infty }\mu _{n}(A)=\mu (A)}$

holds for all Borel sets with , where denotes the topological boundary of . ${\displaystyle A}$ ${\displaystyle \mu (\partial A)=0}$ ${\displaystyle \partial A}$ ${\displaystyle A}$

The weak convergence of probability measures has an important application in the distribution convergence of random variables, such as occurs in the central limit theorem . Weak convergence of probability measures can be examined with the help of characteristic functions .

Another important question for applications is when one can select weakly convergent partial sequences from sequences of measures, i.e. how the relatively sequence- compact sets of measures can be characterized. According to Prokhorov's theorem , a set of finite measures on a Polish space is relatively compact if and only if it is restricted and tight. Limitation here means that there is and tightness that there is a compact for everyone with for everyone . ${\displaystyle M}$ ${\displaystyle \Omega }$ ${\displaystyle \sup\{\mu (\Omega )\mid \mu \in M\}<\infty }$ ${\displaystyle \varepsilon >0}$ ${\displaystyle K\subseteq \Omega }$ ${\displaystyle \mu (\Omega \setminus K)<\varepsilon }$ ${\displaystyle \mu \in M}$

One variation of the weak convergence for Radon measures is the vague convergence at the

${\displaystyle \lim _{n\to \infty }\int _{\Omega }f\,\mathrm {d} \mu _{n}=\int _{\Omega }f\,\mathrm {d} \mu }$

is required for all continuous functions with a compact carrier.

Applications

integration

In contrast to the construction of the Riemann integral (blue), with the Lebesgue integral (red) areas under function graphs are approximated by linear combinations of the dimensions of Borel sets.

The concept of measure is closely linked to the integration of functions. Modern integral terms , such as the Lebesgue integral and its generalizations, are mostly developed from a basis of weight theory. The fundamental relationship is the equation

${\displaystyle \int _{\Omega }\chi _{A}\,\mathrm {d} \mu =\mu (A)}$,

for all , whereby a measurement space is given and denotes the indicator function of the measurable quantity , i.e. the function with for and otherwise. With the help of the desired linearity and monotony properties, the integration can be gradually reduced to simple functions , then to non-negative measurable functions and finally all real- or complex-valued measurable functions with expand. The latter are called -integrable and their integral is called the (generalized) Lebesgue integral with respect to the measure or, for short, -integral. ${\displaystyle A\in {\mathcal {A}}}$ ${\displaystyle (\Omega ,{\mathcal {A}},\mu )}$ ${\displaystyle \chi _{A}}$ ${\displaystyle A}$ ${\displaystyle \chi _{A}\colon \Omega \to \mathbb {R} }$ ${\displaystyle \chi _{A}(\omega )=1}$ ${\displaystyle \omega \in A}$ ${\displaystyle \chi _{A}(\omega )=0}$ ${\displaystyle f}$ ${\displaystyle \textstyle \int _{\Omega }|f|\,\mathrm {d} \mu <\infty }$ ${\displaystyle \mu }$ ${\displaystyle \textstyle \int _{\Omega }f\,\mathrm {d} \mu }$ ${\displaystyle \mu }$ ${\displaystyle \mu }$

This integral term represents a strong generalization of classic integral terms such as the Riemann integral , because it enables the integration of functions on any dimensional space. Again, this is of great importance in stochastics: there, the integral of a random variable with regard to a given probability measure corresponds to its expected value .

However, there are also advantages for real functions of a real variable compared to the Riemann integral. Above all, the convergence properties should be mentioned here when the limit value formation and integration are swapped, which are described, for example, by the theorem of monotonic convergence and the theorem of majorized convergence .

Rooms with integrable functions

Spaces of integrable functions play as standard spaces of functional analysis an important role. The set of all measurable functions on a measure space that fulfill, i.e. are integrable, forms a vector space . By ${\displaystyle f\colon \Omega \to \mathbb {R} }$ ${\displaystyle (\Omega ,{\mathcal {A}},\mu )}$ ${\displaystyle \textstyle \int _{\Omega }|f|\,\mathrm {d} \mu <\infty }$ ${\displaystyle \mu }$ ${\displaystyle {\mathcal {L}}^{1}(\mu ;\mathbb {R} )}$

${\displaystyle \|f\|_{1}:=\int _{\Omega }|f|\,\mathrm {d} \mu }$

a semi-standard is defined. If one identifies functions from this space with one another, if they differ from one another only on a zero set, one arrives at a normalized space . An analog construction can be carried out more generally with functions for which one can be integrated, and so one arrives at the L ^p spaces with the norm ${\displaystyle {\mathcal {L}}_{1}(\mu ;\mathbb {R} )}$ ${\displaystyle L^{1}(\mu ;\mathbb {R} )}$ ${\displaystyle |f|^{p}}$ ${\displaystyle p\geq 1}$ ${\displaystyle \mu }$ ${\displaystyle L^{p}(\mu ;\mathbb {R} )}$

${\displaystyle \|f\|_{p}:=\left(\int _{\Omega }|f|^{p}\,\mathrm {d} \mu \right)^{1/p}}$.

A central result to which the great importance of these rooms in applications can be attributed is their completeness . So they are for all Banach spaces . In the important special case , the norm even turns out to be induced by a scalar product ; it is therefore a Hilbert space . ${\displaystyle p\geq 1}$ ${\displaystyle p=2}$ ${\displaystyle L^{2}(\mu ;\mathbb {R} )}$

Completely analogously, spaces of complex-valued functions can be defined. Complex spaces are also Hilbert spaces; they play a central role in quantum mechanics , where states of particles are described by elements of a Hilbert space. ${\displaystyle L^{p}}$ ${\displaystyle L^{2}}$

Probability theory

In probability theory, probability measures are used to assign probabilities to random events. Random experiments are described by a probability space , that is, by a measure space whose measure fulfills the additional condition. The basic set , the result space , contains the various results that the experiment can produce. The σ-algebra consists of the events to which the probability measure assigns numbers between and . ${\displaystyle (\Omega ,\Sigma ,P)}$ ${\displaystyle P}$ ${\displaystyle P(\Omega )=1}$ ${\displaystyle \Omega }$ ${\displaystyle \Sigma }$ ${\displaystyle P}$ ${\displaystyle 0}$ ${\displaystyle 1}$

Even the simplest case of a finite result space with the power set as σ-algebra and the uniform distribution defined by has numerous possible applications. It plays a central role in the elementary calculation of probability for the description of Laplace experiments , such as throwing a dice and drawing from an urn , in which all results are assumed to be equally likely. ${\displaystyle \Omega }$ ${\displaystyle P(A)={\tfrac {|A|}{|\Omega |}}}$

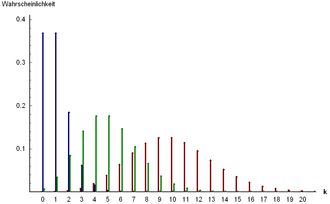
Probability measures are often generated as distributions of random variables , i.e. as image measures . Important examples of probability measures are the binomial and Poisson distributions as well as the geometric and hypergeometric distributions . In the probability measures with Lebesgue density - among other things because of the central limit theorem - the normal distribution has a prominent position. Further examples are the constant uniform distribution or the gamma distribution , which includes numerous other distributions such as the exponential distribution as a special case. ${\displaystyle \mathbb {N} _{0}}$ ${\displaystyle \mathbb {R} }$

The multidimensional normal distribution is also an important example of probability measures on -dimensional Euclidean space . Even more general measure spaces play a role in modern probability theory in the construction of stochastic processes , such as the Wiener measure on a suitable function space for describing the Wiener process ( Brownian movement ), which also has a central position in stochastic analysis . ${\displaystyle d}$ ${\displaystyle \mathbb {R} ^{d}}$

statistics

The basic task of mathematical statistics is to draw conclusions about the distribution of characteristics in a population based on the results of observation of random samples (so-called conclusive statistics). Accordingly, a statistical model contains not only a single probability measure assumed to be known, as in the case of a probability space, but a whole family of probability measures in a common measurement space . The parametric standard models represent an important special case, which are characterized in that the parameters are vectors off and all have a density with respect to a common measure. ${\displaystyle ({\mathcal {X}},{\mathcal {F}},P_{\vartheta }:\vartheta \in \Theta )}$ ${\displaystyle (P_{\vartheta })_{\vartheta \in \Theta }}$ ${\displaystyle ({\mathcal {X}},{\mathcal {F}})}$ ${\displaystyle \mathbb {R} ^{d}}$ ${\displaystyle P_{\vartheta }}$

The parameter and thus the dimension should now be inferred from the observation of . In classical statistics, this takes place in the form of point estimators , which are constructed with the help of estimating functions , or with confidence ranges that contain the unknown parameter with a given probability. With the help of statistical tests , hypotheses about the unknown probability measure can also be tested. ${\displaystyle x\in {\mathcal {X}}}$ ${\displaystyle \vartheta }$ ${\displaystyle P_{\vartheta }}$

In contrast, in Bayesian statistics, distribution parameters are not modeled as unknowns, but rather as random. For this purpose, based on an assumed a priori distribution , an a posteriori distribution of the parameter is determined with the aid of the additional information obtained from the observation results . These distributions are generally measures of probability on the parameter space ; for a priori distributions, however, general measures may also come into question under certain circumstances (so-called improper a priori distributions). ${\displaystyle \Theta }$

Financial math

Modern financial mathematics uses methods of probability theory, particularly stochastic processes , to model the development of the prices of financial instruments over time . A central issue is the calculation of fair prices for derivatives .

A change in size - shown here by different color intensities - can transform a Wiener process with drift (left) into a martingale (right).

A typical feature here is the consideration of different probability measures on the same measurement space: in addition to the real measure determined by the risk appetite of the market participants, risk-neutral measures are used. Fair prices then result as expected values ​​of discounted payments with regard to a risk-neutral measure. In arbitrage-free and perfect market models this existence and uniqueness risk neutral measure is ensured.

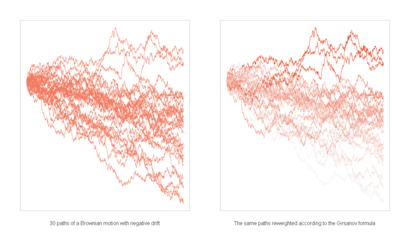
While simple discrete-time and price-discrete models can already be analyzed with elementary probability theory, modern methods of martingale theory and stochastic analysis are necessary , especially for continuous models such as the Black-Scholes model and its generalizations . Equivalent martingale dimensions are used as risk-neutral dimensions. These are probability measures that have a positive density with respect to the real risky measure and for which the discounted price process is a martingale (or more generally a local martingale ). For example, Girsanow's theorem , which describes the behavior of Wiener processes when the measure changes, is of importance here.

Generalizations

The concept of measure allows numerous generalizations in different directions. For the purposes of this article, a measure is therefore sometimes called a positive measure or, more precisely, σ-additive positive measure in the literature .

By weakening the properties required in the definition, functions are obtained that are regarded as preliminary stages of measures in measure theory. The most general term is that of a (non-negative) set function , i.e. a function that assigns values to the sets of a set system over a basic set , whereby it is usually still required that the empty set get the value zero. A content is a finitely additive set function; a σ-additive content is called a premeasure . The Jordan content on the Jordan-measurable subsets of is an application example for an additive set function, which however is not σ-additive. A measure is thus a premeasure whose domain is a σ-algebra. Outer dimensions , that amount functions that monotonously and σ- sub are additive, are an important intermediate in the construction of measures from Prämaßen according Carathéodory represents: a premeasure on a quantity ring is initially continued to an outer dimension around the power set, the restriction on measurable amounts result in a measure. ${\displaystyle [0,\infty ]}$ ${\displaystyle \mathbb {R} ^{d}}$

Other generalizations of the concept of measure are obtained if one gives up the requirement that the values must be in, but the other properties are retained. Negative values ​​are also permitted for a signed measure , i.e. it can assume values ​​in the interval (alternatively also ). With complex numbers as a range of values ​​one speaks of a complex measure . However, the value is not permitted here, that is, a positive measure is always a signed measure, but only finite measures can also be understood as complex measures. In contrast to positive dimensions, the signed and the complex dimensions form a vector space over a measurement space. According to Riesz-Markow's theory of representation, such spaces play an important role as dual spaces of spaces of continuous functions. Signed and complex measures can be written as linear combinations of positive measures according to the decomposition theorem of Hahn and Jordan . And the Radon-Nikodym theorem remains valid for them. ${\displaystyle [0,\infty ]}$ ${\displaystyle (-\infty ,\infty ]}$ ${\displaystyle [-\infty ,\infty )}$ ${\displaystyle \infty }$

Measures with values ​​in arbitrary Banach spaces, the so-called vectorial measures, represent an even further generalization . Measures on the real numbers, the values ​​of which are orthogonal projections of a Hilbert space, so-called spectral measures , are used in the spectral theorem to represent self-adjoint operators , which, among other things, plays an important role in the mathematical description of quantum mechanics (see also Positive Operator Valued Probability Measure ). Measures with orthogonal values are Hilbert space-valued measures in which the measures of disjoint sets are orthogonal to one another. With their help, spectral representations of stationary time series and stationary stochastic processes can be given.

Random measures are random variables whose values ​​are measures. For example, they are used in stochastic geometry to describe random geometric structures. In the case of stochastic processes whose paths have jumps , such as the Lévy processes , the distributions of these jumps can be represented by random counting measures.

literature

• Heinz Bauer : Measure and integration theory. 2nd Edition. De Gruyter, Berlin 1992, ISBN 3-11-013626-0 (hardcover), ISBN 3-11-013625-2 (paperback).
• Martin Brokate , Götz Kersting: Measure and Integral. Birkhäuser, Basel 2011, ISBN 978-3-7643-9972-6 .
• Jürgen Elstrodt : Measure and integration theory. 7th edition. Springer, Berlin / Heidelberg 2011, ISBN 978-3-642-17904-4 .
• Paul R. Halmos : Measure Theory. Springer, Berlin / Heidelberg / New York 1974, ISBN 3-540-90088-8 .
• Achim Klenke: Probability Theory. 2nd Edition. Springer, Berlin / Heidelberg 2008, ISBN 978-3-540-76317-8 .
• Norbert Kusolitsch: Measure and probability theory. An introduction. Springer, Vienna 2011, ISBN 978-3-7091-0684-6 .
• Klaus D. Schmidt: Measure and Probability. 2nd Edition. Springer, Berlin / Heidelberg 2011, ISBN 978-3-642-21025-9 .
• Walter Rudin : Real and Complex Analysis. 2nd Edition. Oldenbourg, Munich 2009, ISBN 978-3-486-59186-6 .
• Dirk Werner : Introduction to Higher Analysis. 2nd Edition. Springer, Berlin / Heidelberg 2009, ISBN 978-3-540-79599-5 .

Web links

• VV Sazonov: Measure . In: Michiel Hazewinkel (Ed.): Encyclopaedia of Mathematics . Springer-Verlag , Berlin 2002, ISBN 978-1-55608-010-4 (English, online ).
• David Jao, Andrew Archibald: measure . In: PlanetMath . (English)
• Eric W. Weisstein : Measure . In: MathWorld (English).

Individual evidence

1. ↑ Elstrodt: Measure and Integration Theory. 2011, pp. 33-34.
2. ↑ Elstrodt: Measure and Integration Theory. 2011, p. 5.
3. ↑ Elstrodt: Measure and Integration Theory. 2011, p. 34.
4. ↑ Brokate, Kersting: Measure and Integral. 2011, p. 19.
5. ^ Werner: Introduction to higher analysis. 2009, p. 215.
6. ^ Werner: Introduction to higher analysis. 2009, p. 222.
7. ^ Werner: Introduction to higher analysis. 2009, p. 226.
8. ↑ Elstrodt: Measure and Integration Theory. 2011, pp. 63-65.
9. ↑ Elstrodt: Measure and Integration Theory. 2011, Chapter II, § 3.
10. ↑ Elstrodt: Measure and Integration Theory. 2011, Chapter II, § 8.
11. ↑ Klenke: Probability Theory. 2008, p. 33.
12. ↑ Klenke: Probability Theory. 2008, p. 43.
13. ↑ Elstrodt: Measure and Integration Theory. 2011, Chapter V.
14. ↑ Klenke: Probability Theory. 2008, chapter 14.
15. ↑ Elstrodt: Measure and Integration Theory. 2011, p. 313.
16. ↑ Elstrodt: Measure and Integration Theory. 2011, p. 319.
17. ↑ Elstrodt: Measure and Integration Theory. 2011, p. 320.
18. ↑ Elstrodt: Measure and Integration Theory. 2011, pp. 351-377.
19. ↑ Elstrodt: Measure and Integration Theory. 2011, p. 385.
20. ↑ Elstrodt: Measure and Integration Theory. 2011, p. 398.
21. ^ Werner: Introduction to higher analysis. 2009, Section IV.5.
22. ↑ Klenke: Probability Theory. 2008, 104ff.
23. ^ Werner: Introduction to higher analysis. 2009, section IV.6.
24. ↑ Dirk Werner: Functional Analysis. 6th edition. Springer, Berlin / Heidelberg 2007, ISBN 978-3-540-72533-6 , p. 13 ff.
25. ↑ Klenke: Probability Theory. 2008.
26. ↑ Hans-Otto Georgii: Stochastics: Introduction to Probability Theory and Statistics. 4th edition. de Gruyter textbook, Berlin 2009, ISBN 978-3-11-021526-7 , p. 196ff.
27. ↑ Hans-Otto Georgii: Stochastics: Introduction to Probability Theory and Statistics. 4th edition. de Gruyter textbook, Berlin 2009, ISBN 978-3-11-021526-7 , part II.
28. ^ Albrecht Irle: Finanzmathematik. The valuation of derivatives. 3. Edition. Springer Spectrum, Wiesbaden 2012, ISBN 978-3-8348-1574-3 .
29. ^ Werner: Introduction to higher analysis. 2009, pp. 214-215.
30. ^ Werner: Introduction to higher analysis. 2009, section IV.3.
31. ↑ Rudin: Real and Complex Analysis. 2009, chapter 6.
32. ↑ Dirk Werner: Functional Analysis. 6th edition. Springer, Berlin / Heidelberg 2007, ISBN 978-3-540-72533-6 , Chapter VII.
33. ↑ Jens-Peter Kreiß, Georg Neuhaus: Introduction to time series analysis. Springer, Berlin / Heidelberg 2006, ISBN 3-540-25628-8 , chapter 5.