Distribution function
The distribution function is a special real function in stochastics and a central concept in the investigation of probability distributions on the real numbers . A distribution function can be assigned to every probability distribution and every real-valued random variable . The value of the distribution function clearly corresponds to the probability that the associated random variable assumes a value less than or equal to. If, for example, the distribution of shoe sizes in Europe is given, the value of the corresponding distribution function at 45 corresponds to the probability that any European has shoe size 45 or smaller.
The distribution function gets its meaning from the correspondence theorem , which states that every distribution function can be assigned a probability distribution on the real numbers and vice versa. The assignment is bijective . This makes it possible, instead of examining probability distributions as set functions on a complex set system, to examine the corresponding distribution functions using methods of measure theory . These are real functions and therefore more easily accessible using the methods of real analysis .
Alternative names include the cumulative distribution function , as it accumulates the probabilities less than being, see also cumulative frequency . Furthermore, it is also referred to as the univariate distribution function for better differentiation from its higher-dimensional counterpart, the multivariate distribution function . In contrast to the more general concept of a distribution function based on the theory of measure , the terms are used as a probability-theoretical distribution function or as a distribution function in the narrower sense .
The equivalent of the distribution function in descriptive statistics is the empirical distribution or cumulative frequency function .
definition
Definition using a probability measure
Given a probability measure on the event space of the real numbers , i. that is, any real number can be interpreted as a possible result . Then the function is called
defined by
the distribution function of . In other words: The function indicates the probability with which a result from the set (all real numbers less than or equal ) occurs.
Definition using a random variable
If it is a real random variable , it is called the function
the distribution function of . The probability denotes that a value is less than or equal to.
Thus the distribution function of a random variable is exactly the distribution function of its distribution .
Examples
Probability measures with densities
If the probability measure has a probability density , then applies
- .
Thus in this case the distribution function has the representation
- .
For example, the exponential distribution has density
- .
So if the random variable is exponentially distributed, so then is
- .
However, this approach is not generally feasible. Firstly, not all probability measures on the real numbers have a density function (e.g. discrete distributions, understood as distributions in ), secondly, even if a density function does exist, there does not necessarily have to be an antiderivative with a closed representation (as is the case with the normal distribution, for example ).
Discrete measures of probability
If one considers a Bernoulli-distributed random variable for a parameter , then
and for the distribution function then follows
More generally, if a random variable with values in the nonnegative integers , then
- .
The rounding function denotes , that is , the largest whole number that is less than or equal to .
Properties and relationship to distribution
Every distribution function has the following properties:
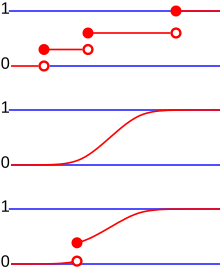
- is monotonically increasing .
- is continuous on the right .
- and .
In addition, any function that fulfills properties 1, 2 and 3 is a distribution function. Consequently, the distribution function can be characterized with the aid of the three properties. For every distribution function there is exactly such a probability measure that applies to all :
Conversely, for every probability measure there is a distribution function such that it applies to all :
Hence the correspondence between and . This fact is also called a correspondence sentence in the literature .
Every distribution function has at most a countable number of jump points.
Since every distribution function is right-continuous, the right-hand limit also exists and it applies to all :
Therefore is continuous if and only applies to all .
Calculating with distribution functions
Given a distribution function, the probabilities can be determined as follows:
- and and
- as well .
It then also follows
- and
for .
In general, the type of inequality sign ( or ) or the type of interval limits (open, closed, left / right half-open) cannot be neglected. This leads to errors, especially in the case of discrete probability distributions , since there can also be a probability on individual points that is then accidentally added or forgotten.
In the case of constant probability distributions , in particular also those that are defined via a probability density function ( absolute continuous probability distributions ), a change in the inequality signs or interval limits does not lead to errors.
- example
When rolling the dice, the probability of rolling a number between 2 (exclusive) and 5 inclusive is calculated
- .
convergence
definition
A sequence of distribution functions is called weakly convergent to the distribution function if
- applies to all where is continuous.
The terms convergent in distribution or stochastically convergent can also be found for distribution functions of random variables .
properties
Using the Helly-Bray theorem, a bridge to the weak convergence of measures can be built via the weak convergence of the distribution functions . Because a sequence of probability measures is weakly convergent if and only if the sequence of its distribution functions converges weakly. Analogously, a sequence of random variables is precisely then convergent in distribution if the sequence of its distribution functions converges weakly.
Some authors use this equivalence to define convergence in distribution because it is more accessible than the weak convergence of probability measures. The statement of Helly-Bray 's theorem can also be found in part in the Portmanteau theorem .
For distribution functions in the sense of measure theory , the definition given above is not correct, but corresponds to the vague convergence of distribution functions (in the sense of measure theory) . For probability measures, however, this coincides with the weak convergence of distribution functions . The weak convergence of distribution functions is metrized by the Lévy distance .
Classification of probability distributions using distribution functions
Probability distributions whose distribution function is continuous are called continuous probability distributions . They can be further subdivided into
- Absolutely continuous probability distributions for which a probability density function exists. Typical examples of this would be the normal distribution or the exponential distribution .
- Continuously singular probability distributions that have no probability density function. An example of this would be the Cantor distribution .
For absolutely continuous probability distributions, the derivative of the distribution function corresponds to the probability density function. Absolutely continuous probability distributions can be differentiated almost everywhere, but their derivation is almost everywhere zero.
Distribution functions of discrete probability distributions are characterized by their jumps between the areas with constant function values. They are jump functions .
Alternative definition
Continuous distribution functions on the left
In the sphere of influence of Kolmogorov's tradition , namely the mathematical literature of the former " Eastern Bloc ", there has been another convention of the distribution function that has been used up until the recent past, parallel to the "less or equal" convention that is prevalent today, which instead of the less than or equal sign is real -lower characters used, so
In the case of continuous probability distributions, the two definitions match, in the case of discrete distributions, on the other hand, they differ in that the distribution function in the case of the “true-less” convention is not continuous on the right-hand side, but on the left-hand side.
example
For the binomial distribution , for example, the “less than or equal” convention that is common today results in a distribution function of the form
- ,
in the case of the “really smaller” convention, however, the spelling
- .
So in the second case especially applies to
- .
Related concepts
Empirical distribution function
The empirical distribution function of a sample plays an important role in statistics. Formally, it corresponds to the distribution function of a discrete uniform distribution on the points . It is important because, according to the Gliwenko-Cantelli theorem, the empirical distribution function of an independent sample of random numbers converges against the distribution function of the probability distribution by means of which the random numbers were generated.
Common distribution function and edge distribution functions
The common distribution function generalizes the concept of a distribution function from the distribution of a random variable to the common distribution of random variables . The concept of marginal distribution can also be transferred to the marginal distribution function . These distribution functions have in common that their domain is for
Generalized inverse distribution function
The generalized inverse distribution function may be an inverse function of the distribution function and is important for determining quantiles .
Distribution function in terms of measure theory
Distribution functions can be defined not only for probability measures, but for arbitrary finite measures on the real numbers. In these distribution functions (in the sense of measure theory) important properties of the measures are then reflected. They form a generalization of the distribution functions discussed here.
Survival function
In contrast to a distribution function, the survival function indicates how high the probability is of exceeding a certain value. It occurs, for example, when modeling lifetimes and indicates the probability of “surviving” a certain point in time.
Multivariate and multidimensional distribution function
The multivariate distribution function is the distribution function associated with multivariate probability distributions. In contrast, the higher-dimensional counterpart of the distribution function in the sense of measure theory is usually referred to as the multi-dimensional distribution function .
literature
- Klaus D. Schmidt: Measure and Probability . 2nd, revised edition. Springer-Verlag, Heidelberg / Dordrecht / London / New York 2011, ISBN 978-3-642-21025-9 , doi : 10.1007 / 978-3-642-21026-6 .
- Achim Klenke : Probability Theory . 3. Edition. Springer-Verlag, Berlin / Heidelberg 2013, ISBN 978-3-642-36017-6 , doi : 10.1007 / 978-3-642-36018-3 .
- Norbert Kusolitsch: Measure and probability theory . An introduction. 2nd, revised and expanded edition. Springer-Verlag, Berlin / Heidelberg 2014, ISBN 978-3-642-45386-1 , doi : 10.1007 / 978-3-642-45387-8 .
Individual evidence
- ^ Schmidt: Measure and probability. 2011, p. 246.
- ↑ Kusolitsch: Measure and probability theory. 2014, p. 62.
- ↑ N. Schmitz. Lectures on probability theory. Teubner, 1996.
- ^ Schmidt: Measure and probability. 2011, p. 396.
- ↑ Kusolitsch: Measure and probability theory. 2014, p. 287.
- ↑ Alexandr Alexejewitsch Borowkow: Rachunek prawdopodobieństwa. Państwowe Wydawnictwo Naukowe, Warszawa 1977, p. 36 ff.
- ^ Marek Fisz : Probability calculation and mathematical statistics. VEB Deutscher Verlag der Wissenschaften, eleventh edition, Berlin 1989, definition 2.2.1, p. 51.
- ^ W. Gellert, H. Küstner, M. Hellwich, H. Kästner (eds.): Small encyclopedia of mathematics. VEB Verlag Enzyklopädie Leipzig 1970, OCLC 174754758 , pp. 659-660.



![{\ displaystyle F_ {P} \ colon \ mathbb {R} \ to [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d2e428d6aaa54fa25289ec92f0fe95e8057387e)
![{\ displaystyle F_ {P} (x) = P ((- \ infty, x])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bef8e83eb5201467cbb2dcd0afe44971d70ca95a)
![{\ displaystyle (- \ infty, x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad2402c0ff48631309599dc5d8be7607fb994d8d)



![{\ displaystyle P ((a, b]) = \ int _ {a} ^ {b} f_ {P} (x) \, \ mathrm {d} x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ddd9cfff49a23ceb40a6bb483b3f06bd5aa24b84)












![F \ colon \ mathbb {R} \ rightarrow [0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4c45b6faf38bb3fb300ab4678d3675afd172f56)



![{\ displaystyle P_ {F} \ colon {\ mathcal {B}} (\ mathbb {R}) \ to [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f028a26b4d83d4e753de7e2f078ae55d55904097)

![{\ displaystyle P_ {F} \ left (] - \ infty, x] \ right) = F (x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a1576e643e0cf9c3848df80fae46fac65f09378)
![{\ displaystyle P \ colon {\ mathcal {B}} (\ mathbb {R}) \ to [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/914424c5a0da8466438e221a5d22de2aab4ef610)
![{\ displaystyle F_ {P} \ colon \ mathbb {R} \ rightarrow [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f8c0dd4c1038f93abe968e70d19b188b7f29332c)
![{\ displaystyle P \ left (] - \ infty, x] \ right) = F_ {P} (x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0405857991ccd542fbd42ff0857e57154b7a084b)






![{\ displaystyle P ((- \ infty; a]) = F (a)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c87fb872c6a3251f82fd21f908111708d1489a8)


![{\ displaystyle P ((a; b]) = F (b) -F (a)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fcc1d1c84afe5749824309e68d2c1aa581dcf21d)













