Marginal distribution

Representation of the standard deviation ellipse of a two-dimensional normal distribution , as well as the two marginal distributions (red and blue).

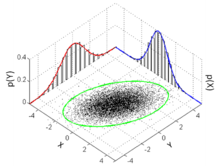
As marginal distributions or marginal distribution in the are stochastic , the probability distributions of sub-families of a given family of random variables , respectively. The distribution of the entire family is also called the joint distribution of the random variables for clarity . For example, if and are random variables (on the same probability space ), then the distributions of the individual variables and the marginal distributions of the random vector are called . ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle (X,Y)}$

Marginal distributions can be calculated for both discrete and continuous features. As with distributions in general, one differentiates accordingly:

• discrete marginal distributions
• continuous marginal distributions

In addition, the marginal distribution can be formed for both absolute frequencies and relative frequencies . The individual values ​​of the marginal distribution are then called marginal frequencies (also marginal frequencies or marginal frequencies). The marginal frequencies for categorically subdivided (distinct) features can be read off the margin of a contingency table . Here they are the sums of the frequencies across the neglected feature.

Example using contingency tables

Marginal distributions of discrete features can be represented in contingency tables. At the edge of this table, the edge frequencies, which together form the edge distribution, can be read off as sums of the neglected feature.

For example, a contingency table with absolute frequencies can be seen here. The same would also be conceivable with relative frequencies.

	man	woman	Marginal frequencies
grade 10	10	10	20th
11th grade	4th	16	20th
Marginal frequencies	14th	26th	40

The marginal frequency of being in class 10, neglecting whether one is male or female, is 20. The corresponding marginal frequency for class 11 is also 20. The marginal distribution is evenly distributed because there are the same number of students in both classes. The attribute class is distinct, that is, divided into clearly defined categories.

However, there are also characteristics that are not divided into categories, such as height. These features are continuous because there are smooth transitions between all possible manifestations of the feature. Such characteristics cannot be represented in tables. In order to still enable the representation in a contingency table, it is possible to divide the characteristic into classes (here, categories are meant) by defining so-called class boundaries. One could divide the constant characteristic of height by setting 142 cm as the class boundary and dividing people into people taller than 142 cm and not taller than 142 cm. For these groups, which are divided into classes, class frequencies can now be measured again , which are entered in a contingency table. Since a person who is in one class (> 142) cannot be in another class (≤ 142) at the same time, one speaks of a division into disjoint sets.

definition

A higher-dimensional random variable with a multivariate distribution as a probability measure is given . Then it's called the distribution ${\displaystyle Z=(X_{1},\dotsc ,X_{n})}$ ${\displaystyle P_{Z}}$

${\displaystyle P_{X_{i}}(A):=P_{Z}(\Omega _{1}\times \dotsb \times \Omega _{i-1}\times A\times \Omega _{i+1}\times \dotsb \times \Omega _{n})}$

the i-th marginal distribution or the i-th marginal distribution of . Alternatively, it is also defined as ${\displaystyle Z}$

${\displaystyle P_{X_{i}}(A)=P(X_{1}\in \Omega _{1},\dotsc ,X_{i-1}\in \Omega _{i-1},X_{i}\in A,X_{i+1}\in \Omega _{i+1},\dotsc ,X_{n}\in \Omega _{n})}$.

In the two-dimensional with would be the first marginal distribution ${\displaystyle Z=(X,Y)}$

${\displaystyle P_{X}(A)=P_{Z}(A\times \Omega _{2}){\text{ bzw. }}P_{X}(A)=P(X\in A,Y\in \Omega _{2})}$.

More generally, marginal distributions can also be defined for each subset . If , they are called m-dimensional marginal distributions. They are then defined by ${\displaystyle J\subset I=\{1,\dotsc ,n\}}$ ${\displaystyle |J|=m}$

${\displaystyle P_{X_{J}}(A)\;=\;{\begin{cases}P(X_{i}\in A_{i})&{\mbox{wenn }}i\in J\\X_{i}\in \Omega _{i}&{\mbox{sonst.}}\end{cases}}}$

For

${\displaystyle A=\prod _{i\in J}A_{i}}$.

Elementary properties

• Exactly m-dimensional marginal distributions exist . ${\displaystyle {\tbinom {n}{m}}}$
• From the point of view of dimension theory, marginal distributions are the image dimensions under the projections onto one or more coordinates.
• If the stochastically independent random variables are , then the joint distribution of is exactly the product of the one-dimensional marginal distributions. ${\displaystyle X_{i}}$ ${\displaystyle X_{i}}$

Derived terms

Edge distribution function

If the distribution function has , an edge distribution function can also be specified as a distribution function of the edge distributions. For the one-dimensional marginal distributions it is defined as ${\displaystyle Z}$ ${\displaystyle F_{Z}\colon \mathbb {R} ^{n}\to [0,1]}$

${\displaystyle F_{X_{i}}(x_{i})=F_{Z}(\infty ,\dotsc ,\infty ,x_{i},\infty ,\dotsc ,\infty )}$.

All components except for the i-th are therefore set to infinity. One proceeds analogously for the m-dimensional boundary distribution functions. All components in are retained, all others are set to infinity. The first marginal distribution function then results for the two-dimensional case with ${\displaystyle J}$ ${\displaystyle Z=(X,Y)}$

${\displaystyle F_{X}(x)=F_{Z}(x,\infty )}$.

Edge density

Likewise, probability densities can also be specified for marginal distributions , which are called marginal densities . Those are the functions for which ${\displaystyle f_{X_{i}}}$

${\displaystyle F_{X_{i}}(x_{i})=\int _{-\infty }^{x_{i}}f_{X_{i}}(t)\ \mathrm {d} t}$

applies. Has a common density , the edge density can also be called ${\displaystyle Z}$ ${\displaystyle f_{Z}(x_{1},\dotsc ,x_{n})}$

${\displaystyle f_{X_{i}}(x_{i}):=\int _{-\infty }^{\infty }\dotsi \int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\dotsi \int _{-\infty }^{\infty }f_{Z}(x_{1},\dotsc ,x_{i-1},x_{i},x_{i+1},\dotsc ,x_{n})\ \mathrm {d} x_{1}\dotsm \mathrm {d} x_{i-1}\mathrm {d} x_{i+1}\dotsm \mathrm {d} x_{n}}$

define. For m-dimensional edge densities one proceeds analogously, one then integrates over all components that are not contained in. In the two-dimensional with , one then obtains by means of integration over the respective other component as edge densities ${\displaystyle J}$ ${\displaystyle Z=(X,Y)}$

${\displaystyle f_{X}(x)=\int _{-\infty }^{\infty }f_{Z}(x,y)\ \mathrm {d} y}$

${\displaystyle f_{Y}(y)=\int _{-\infty }^{\infty }f_{Z}(x,y)\ \mathrm {d} x}$

Edge probability function

Just as edge densities, edge probability functions can also be specified. Essentially, only the integration is replaced by the summation. Has a common probability function , the i-th edge probability function is given as ${\displaystyle Z}$ ${\displaystyle f_{Z}(x_{1},\dotsc ,x_{n})}$

${\displaystyle f_{X_{i}}(x_{i})=\sum _{j\neq i \atop x_{j}\in \mathbb {Z} }f_{Z}(x_{1},\dotsc ,x_{n})}$.

The m-dimensional marginal distributions are also obtained by summation if the components of interest are not also summed. In two-dimensional with it then results ${\displaystyle Z=(X,Y)}$

${\displaystyle f_{X}(x_{i})=\sum _{k\in K}f_{Z}(x_{i},y_{k})}$

${\displaystyle f_{Y}(y_{k})=\sum _{i\in I}f_{Z}(x_{i},y_{k})}$.

Example multinomial distribution

In two dimensions

Be an example two-dimensional multinomialverteilt so . So has the probability function ${\displaystyle Z=(X,Y)}$ ${\displaystyle Z\sim M(n,(p,1-p))}$ ${\displaystyle Z}$

${\displaystyle f_{Z}(x,y)\;=\;{\begin{cases}{n \choose x,y}\;p^{x}(1-p)^{y}&{\mbox{wenn }}x+y=n\\0&{\mbox{sonst.}}\end{cases}}}$.

Here is the multinomial coefficient . If you place it , it results directly ${\displaystyle {n \choose x,y}}$ ${\displaystyle y=n-x}$

${\displaystyle f_{Z}(x,y)={n \choose x}p^{x}(1-p)^{n-x}}$.

The probability function can therefore be represented independently of . Accordingly, the edge density of , which arises by adding up over all, is again exactly the probability function of , but without as a variable. So it is ${\displaystyle y}$ ${\displaystyle X}$ ${\displaystyle y}$ ${\displaystyle Z}$ ${\displaystyle y}$

${\displaystyle f_{X}(x)={n \choose x}p^{x}(1-p)^{n-x}}$,

the marginal distribution of the multionomial distribution is thus a binomial distribution with the parameters and . ${\displaystyle p}$ ${\displaystyle n}$

In several dimensions

Let and -dimensional multinomial distribution, i.e. with . The probability function is then ${\displaystyle Z=(X_{1},\dotsc ,X_{m})}$ ${\displaystyle m}$ ${\displaystyle Z\sim M(n,(p_{1},\dotsc ,p_{m}))}$ ${\displaystyle p_{1}+\dotsb +p_{m}=1}$

${\displaystyle f_{Z}(x_{1},\dotsc ,x_{m})\;=\;{\begin{cases}{n \choose x_{1},\dotsc ,x_{m}}\;p_{1}^{x_{1}}\dotsm p_{k}^{x_{m}}&{\mbox{wenn }}x_{1},\dotsc ,x_{k}\in \mathbb {N} _{0}{\mbox{ und }}x_{1}+\dotsb +x_{m}=n\\0&{\mbox{sonst}}\end{cases}}}$.

To calculate the first marginal distribution one now adds up over all . To simplify the calculation, group and . With the help of the multinomial theorem it then follows that the marginal distribution is again binomially distributed with the parameters and . ${\displaystyle x_{2},x_{3},\dotsc ,x_{m}}$ ${\displaystyle p_{2}+\dotsb +p_{m}=1-p_{1}}$ ${\displaystyle x_{1}=n-(x_{2}+\dotsb +x_{3})}$ ${\displaystyle n}$ ${\displaystyle p_{1}}$

Related concepts

Often, on the one hand, marginal distributions are to be generated with a special distribution . On the other hand, the common distribution of random variables and their dependencies should be shown correctly. Such multivariate distributions are not only described by the marginal distributions and the correlation , rather the dependency often has to be described and modeled more precisely. For example, when modeling bond returns, one might expect that the spread between the two returns also remains within a plausible range. Therefore, when modeling multivariate distributions, it is often necessary or useful to model the marginal distributions and their interdependence separately. This is done by calibrating a copula .

Using the marginal distributions, the conditional distribution can be determined from a multivariate distribution . It models that there is already knowledge about the value of a random variable.

literature

• IN Bronstein: Paperback of Mathematics. Publisher Harri Deutsch, ISBN 3-8171-2006-0 .
• Norbert Henze : Stochastics for Beginners: An Introduction to the Fascinating World of Chance. Vieweg + Teubner Verlag 2010, ISBN 978-3-8348-0815-8 , doi: 10.1007 / 978-3-8348-9351-2 .
• Christian Hesse: Applied probability theory . 1st edition. Vieweg, Wiesbaden 2003, ISBN 3-528-03183-2 , doi : 10.1007 / 978-3-663-01244-3 .

Individual evidence

1. ↑ P. Heinz Müller (Ed.): Probability calculation and mathematical statistics. Lexicon of Stochastics. Akademie-Verlag, Berlin 1980, p. 116 and p. 124.