Probability function

Probability function of a fair dice. All numbers have the same probability 1/6.

A probability function , also called counting density , is a special real-valued function in stochastics . Probability functions are used to construct and examine probability distributions , more precisely discrete probability distributions . Each discrete probability distribution can be assigned a unique probability function. Conversely, each probability function defines a uniquely determined discrete probability distribution.

In most cases, probability functions are defined on the natural numbers . You then assign each number the probability that that number will occur. For example, when modeling a fair dice, the probability function would assign the value to the numbers from one to six and zero to all others. ${\displaystyle {\tfrac {1}{6}}}$

From the point of view of measure theory , probability functions are special density functions (in the sense of measure theory) with regard to the counting measure . In a more general context, these are also called weight functions.

definition

Definition of probability function : For a discrete random variable , the probability function for is defined by ${\displaystyle X}$ ${\displaystyle f(x)}$ ${\displaystyle x\in \mathbb {R} }$

${\displaystyle f(x)={\begin{cases}P(X=x_{i})=p_{i},&x=x_{i}\in \{x_{1},x_{2},\dots ,x_{k}\dots \}\\0,&{\text{ sonst.}}\end{cases}}}$

One writes “for all others ”, or otherwise as an abbreviation for “other ”. ${\displaystyle x}$ ${\displaystyle x}$

For the construction of probability distributions

Given a function

${\displaystyle f\colon \mathbb {N} _{0}\to \mathbb {R} }$,

for which applies

• It is for everyone . The function assigns a real number between zero and one to every natural number . ${\displaystyle f(i)\in [0,1]}$ ${\displaystyle i\in \mathbb {N} _{0}}$ ${\displaystyle f}$
• ${\displaystyle f}$is normalized in the sense that the function values ​​add up to one. So it applies

${\displaystyle \sum _{i=0}^{\infty }f(i)=1}$.

Then a probability function is called and defined by ${\displaystyle f}$

${\displaystyle P(\{i\}):=f(i)}$ for all ${\displaystyle i\in \mathbb {N} _{0}}$

a uniquely determined probability distribution on the natural numbers , provided with the power set as the event system . ${\displaystyle P}$ ${\displaystyle \mathbb {N} _{0}}$ ${\displaystyle {\mathcal {P}}(\mathbb {N} _{0})}$

Derived from probability distributions

Given a probability distribution on the natural numbers , provided with , and be a random variable with values ​​in . Then is called ${\displaystyle P}$ ${\displaystyle \mathbb {N} _{0}}$ ${\displaystyle {\mathcal {P}}(\mathbb {N} _{0})}$ ${\displaystyle X}$ ${\displaystyle \mathbb {N} _{0}}$

${\displaystyle f_{P}\colon \mathbb {N} _{0}\to \mathbb {R} }$

defined by

${\displaystyle f_{P}(i):=P(\{i\})}$

the probability function of . Analog means ${\displaystyle P}$

${\displaystyle f_{X}\colon \mathbb {N} _{0}\to \mathbb {R} }$

defined by

${\displaystyle f_{X}(i):=P(X=i)}$

the probability function of ${\displaystyle X}$

Examples

A typical probability function is

${\displaystyle f_{n,p}(k)={\begin{cases}{\binom {n}{k}}p^{k}(1-p)^{n-k}&{\text{ für }}k\in \{0,1,\dots ,n\}\\0&{\text{ sonst}}\end{cases}}}$

for a natural number and a real number . The normalization here follows directly from the binomial theorem , because it is ${\displaystyle n}$ ${\displaystyle p\in (0,1)}$

${\displaystyle \sum _{k=0}^{\infty }f_{n,p}(k)=\sum _{k=0}^{n}{\binom {n}{k}}p^{k}(1-p)^{n-k}=((1-p)+p)^{n}=1}$.

The probability distribution generated in this way is the binomial distribution .

Another classic probability function is

${\displaystyle f_{p}(k)=p(1-p)^{k}}$ For ${\displaystyle k\in \{0,1,2,\dots \}}$

and a . Here the normalization follows from the geometric series , because it is ${\displaystyle p\in (0,1)}$

${\displaystyle \sum _{k=0}^{\infty }f_{p}(k)=p\sum _{k=0}^{\infty }(1-p)^{k}={\frac {p}{1-(1-p)}}=1}$.

The probability distribution generated in this way is the geometric distribution .

general definition

The definition can be extended from the natural numbers to arbitrary at most countable sets . Is such a crowd and is ${\displaystyle \Omega }$

${\displaystyle f\colon \Omega \to [0,1]}$

With

${\displaystyle \sum _{i\in \Omega }f(i)=1}$,

so defined by ${\displaystyle f}$

${\displaystyle P(\{i\}):=f(i)}$ for all ${\displaystyle i\in \Omega }$

a clearly determined probability distribution . Conversely, if a probability distribution is and a random variable with values ​​in , then are called ${\displaystyle (\Omega ,{\mathcal {P}}(\Omega ))}$ ${\displaystyle P}$ ${\displaystyle (\Omega ,{\mathcal {P}}(\Omega ))}$ ${\displaystyle X}$ ${\displaystyle \Omega }$

${\displaystyle f_{P}\colon \Omega \to [0,1]}$ defined by ${\displaystyle f_{P}(i):=P(\{i\})}$

and

${\displaystyle f_{X}\colon \Omega \to [0,1]}$ defined by ${\displaystyle f_{X}(i):=P(X=i)}$

the probability function of respectively . ${\displaystyle P}$ ${\displaystyle X}$

Alternative definition

Some authors first define real sequences with for all and ${\displaystyle (p_{i})_{i\in \Omega }}$ ${\displaystyle p_{i}\in [0,1]}$ ${\displaystyle i\in \Omega }$

${\displaystyle \sum _{i\in \Omega }p_{i}=1}$

and call these sequences probability vectors or stochastic sequences .

A probability function is then defined as

${\displaystyle f\colon \Omega \to [0,1]}$

given by

${\displaystyle f(i)=p_{i}}$ for all ${\displaystyle i\in \Omega }$

Conversely, each probability distribution or random variable then also defines a stochastic sequence / probability vector via or ${\displaystyle \Omega }$ ${\displaystyle (P(\{i\}))_{i\in \Omega }}$ ${\displaystyle (P(X=i))_{i\in \Omega }}$

Other authors already call the sequence a counting density. ${\displaystyle (p_{i})_{i\in \Omega }}$

Further examples

A typical example of probability functions on arbitrary sets is the discrete uniform distribution on a finite set . By definition it then has the probability function ${\displaystyle \Omega }$

${\displaystyle f(i)={\tfrac {1}{|\Omega |}}}$for everyone . ${\displaystyle i\in \Omega }$

The access via the stochastic sequences allows the following construction of probability functions: If any (at most countable) sequence of positive real numbers with index set is given for which ${\displaystyle (a_{i})_{i\in \Omega }}$ ${\displaystyle \Omega }$

${\displaystyle \sum _{i\in \Omega }a_{i}<\infty }$

is true, that's how one defines

${\displaystyle c=\sum _{i\in \Omega }a_{i}}$.

Then is a stochastic sequence and thus also defines a probability function. For example, if you look at the episode ${\displaystyle ({\tfrac {a_{i}}{c}})_{i\in \Omega }}$

${\displaystyle a_{k}:={\frac {\lambda ^{k}}{k!}}}$for , ${\displaystyle k\in \mathbb {N} }$

so is

${\displaystyle \sum _{k=0}^{\infty }{\frac {\lambda ^{k}}{k!}}=e^{\lambda }}$.

This is the normalization constant and results as a probability function ${\displaystyle c=e^{\lambda }}$

${\displaystyle f(k)=e^{-\lambda }{\frac {\lambda ^{k}}{k!}}}$.

This is the probability function of the Poisson distribution .

Determination of key figures using probability functions

Many of the important key figures of random variables and probability distributions can be derived directly from the probability function if it exists.

Expected value

If a random variable with values ​​in and probability function , then the expected value is given by ${\displaystyle X}$ ${\displaystyle \mathbb {N} }$ ${\displaystyle f_{X}}$

${\displaystyle \operatorname {E} (X)=\sum _{k=0}^{\infty }k\cdot f_{X}(k)}$.

It always exists, but it can also be infinite. If, more generally, a subset of real numbers that can be counted at most and a random variable with values ​​in and probability function, then the expected value is given by ${\displaystyle \Omega \subset \mathbb {R} }$ ${\displaystyle X}$ ${\displaystyle \Omega }$ ${\displaystyle f_{X}}$

${\displaystyle \operatorname {E} (X)=\sum _{k\in \Omega }k\cdot f_{X}(k)}$

if the sum exists.

Variance

Analogous to the expected value, the variance can also be derived directly from the probability function. Be to it

${\displaystyle \operatorname {E} (X)=\mu }$

the expected value. If then a random variable with values ​​in and probability function , then the variance is given by ${\displaystyle X}$ ${\displaystyle \mathbb {N} }$ ${\displaystyle f_{X}}$

${\displaystyle \operatorname {Var} (X)=\sum _{k=0}^{\infty }(k-\mu )^{2}f_{X}(k)}$

or equivalent to it based on the law of displacement

${\displaystyle \operatorname {Var} (X)=-\mu ^{2}+\sum _{k=0}^{\infty }k^{2}f_{X}(k)}$

Accordingly, in the more general case of a random variable with values ​​in (see above), that ${\displaystyle \Omega }$

${\displaystyle \operatorname {Var} (X)=\sum _{k\in \Omega }(k-\mu )^{2}f_{X}(k)}$

Here, too, all statements only apply if the corresponding sums exist.

mode

For discrete probability distributions, the mode is defined directly via the probability function: If a random variable with values ​​in and probability function or is a probability distribution on with probability function , then a mode or modal value of or , if ${\displaystyle X}$ ${\displaystyle \mathbb {N} }$ ${\displaystyle f}$ ${\displaystyle P}$ ${\displaystyle \mathbb {N} }$ ${\displaystyle f}$ ${\displaystyle k_{\text{mod}}}$ ${\displaystyle X}$ ${\displaystyle P}$

${\displaystyle f(k-1)\leq f(k_{\text{mod}})\geq f(k+1)}$

is. If, more generally, there is an at most countable set , the elements of which are sorted in ascending order, that is , a is called a mode or modal value if ${\displaystyle \Omega }$ ${\displaystyle x_{k}}$ ${\displaystyle \dots <x_{k-1}<x_{k}<x_{k+1}<\dots }$ ${\displaystyle x_{k}}$

${\displaystyle f(x_{k-1})\leq f(x_{k})\geq f(x_{k+1})}$

applies.

Properties and constructive terms

Distribution functions and probability functions

Distribution function of a probability measure that can be defined using a probability function. The distribution function typically has a jump upwards at this point . ${\displaystyle i}$ ${\displaystyle f(i)=P(\{i\})}$

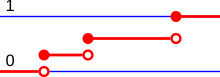
If a probability function is on , then the distribution function of the corresponding probability measure is given as ${\displaystyle f}$ ${\displaystyle \mathbb {N} }$

${\displaystyle F_{P}(x)=\sum _{i=0}^{\lfloor x\rfloor }f(i)}$.

The rounding function denotes , that is , the largest whole number that is less than or equal to . ${\displaystyle \lfloor \cdot \rfloor }$ ${\displaystyle \lfloor x\rfloor }$ ${\displaystyle x}$

If the real numbers are defined on at most a countable subset, i.e. on , then the distribution function of the probability measure is defined by ${\displaystyle f}$ ${\displaystyle A\subset \mathbb {R} }$

${\displaystyle F_{P}(x)=\sum _{i\leq x}f(i)}$.

Example of this is . ${\displaystyle A=\mathbb {Z} }$

Convolution and sum of random variables

For probability distributions with probability functions, the convolution (of probability distributions) can be traced back to the convolution (of functions) of the corresponding probability functions. If probability distributions are with probability functions and , then is ${\displaystyle P,Q}$ ${\displaystyle f_{P}}$ ${\displaystyle f_{Q}}$

${\displaystyle f_{P*Q}=f_{P}*f_{Q}}$.

The convolution of and and denotes the convolution of the functions and . The probability function of the convolution of two probability distributions is thus exactly the convolution of the probability functions of the probability distributions. ${\displaystyle P*Q}$ ${\displaystyle P}$ ${\displaystyle Q}$ ${\displaystyle f*g}$ ${\displaystyle f}$ ${\displaystyle g}$

This property is directly transferred to the sum of stochastically independent random variables . If two stochastically independent random variables with probability functions and are given, then is ${\displaystyle X,Y}$ ${\displaystyle f_{X}}$ ${\displaystyle f_{Y}}$

${\displaystyle f_{X+Y}=f_{X}*f_{Y}}$.

The probability function of the sum is thus the convolution of the probability functions of the individual random variables.

Probability generating function

→ Main article : Probability generating function

A probability-generating function can be assigned to each probability distribution. This is a polynomial or a power series with the probability function as a coefficient. It is thus defined as ${\displaystyle \mathbb {N} }$

${\displaystyle m_{P}(t)=\sum _{k=0}^{\infty }f_{P}(k)t^{k}}$

for the probability function of a probability distribution . The probability-generating function of a random variable is defined analogously. ${\displaystyle f_{P}}$ ${\displaystyle P}$

Probability-generating functions make it easier to investigate and calculate with probability distributions. For example, the probability-generating function of the convolution of two probability distributions is exactly the product of the probability-generating functions of the individual probability distributions. Important key figures such as the expected value and the variance can also be found in the derivatives of the probability-generating functions.

literature

• Hans-Otto Georgii: Stochastics . Introduction to probability theory and statistics. 4th edition. Walter de Gruyter, Berlin 2009, ISBN 978-3-11-021526-7 , doi : 10.1515 / 9783110215274 .
• Achim Klenke: Probability Theory . 3. Edition. Springer-Verlag, Berlin Heidelberg 2013, ISBN 978-3-642-36017-6 , doi : 10.1007 / 978-3-642-36018-3 .
• David Meintrup, Stefan Schäffler: Stochastics . Theory and applications. Springer-Verlag, Berlin Heidelberg New York 2005, ISBN 978-3-540-21676-6 , doi : 10.1007 / b137972 .
• Klaus D. Schmidt: Measure and Probability . 2nd, revised edition. Springer-Verlag, Heidelberg Dordrecht London New York 2011, ISBN 978-3-642-21025-9 , doi : 10.1007 / 978-3-642-21026-6 .
• Claudia Czado, Thorsten Schmidt: Mathematical Statistics . Springer-Verlag, Berlin Heidelberg 2011, ISBN 978-3-642-17260-1 , doi : 10.1007 / 978-3-642-17261-8 .
• Ulrich Krengel : Introduction to probability theory and statistics . For studies, professional practice and teaching. 8th edition. Vieweg, Wiesbaden 2005, ISBN 3-8348-0063-5 , doi : 10.1007 / 978-3-663-09885-0 .

Individual evidence

1. ^ Georgii: Stochastics. 2009, p. 18.
2. ↑ Klenke: Probability Theory. 2013, p. 13.
3. ^ Schmidt: Measure and probability. 2011, p. 196.
4. ↑ Czado, Schmidt: Mathematical Statistics. 2011, p. 4.
5. ↑ Klenke: Probability Theory. 2013, p. 13.
6. ↑ Meintrup, Schäffler: Stochastics. 2005, p. 63.
7. ^ Schmidt: Measure and probability. 2011, p. 234.
8. ^ Georgii: Stochastics. 2009, p. 18.
9. ^ AV Prokhorov: Mode . In: Michiel Hazewinkel (Ed.): Encyclopaedia of Mathematics . Springer-Verlag , Berlin 2002, ISBN 978-1-55608-010-4 (English, online ).