Variance (stochastics)

This article deals with variance as a measure of the distribution of a real random variable. For the variance of a sample, see sample variance , further meanings can be found under variance .

Density functions of two normally distributed random variables (red) and (green) with the same expected value , but different variances. The horizontal axis shows the value, the vertical one the frequency. Since the red curve is narrower around the expected value than the green one , it shows a lower variance ( ). The square root of the variance, the standard deviation, can be read off at the inflection points in the normal distribution . ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle \mu _{X}=\mu _{Y}=0}$ ${\displaystyle f(x)}$ ${\displaystyle f(y)}$ ${\displaystyle \sigma _{X}^{2}<\sigma _{Y}^{2}}$

The variance ( Latin variantia "difference" or variare "(ver) change, be different") is a measure of the spread of the probability density around its center of gravity. Mathematically, it is defined as the mean square deviation of a real random variable from its expected value . It is the central second-order moment of a random variable.

The variance can be interpreted physically as a moment of inertia . It is also the square of the standard deviation , the most important measure of dispersion in stochastics . The variance can be calculated with a variance estimator , e.g. As the sample variance , estimated to be.

The term “variance” was mainly coined by the British statistician Ronald Fisher (1890–1962). Other words for the variance are the outdated dispersion ( Latin dispersio "dispersion" or dispergere "distribute, spread, scatter"), the dispersion square or the scatter .

The properties of variance include that it is never negative and that it does not change as the distribution shifts. The variance of a sum of uncorrelated random variables is equal to the sum of their variances. A disadvantage of the variance for practical applications is that, in contrast to the standard deviation, it has a different unit than the random variable. Since it is defined by an integral , it does not exist for all distributions, ie it can also be infinite .

A generalization of the variance is the covariance . In contrast to the variance, which measures the variability of the random variable under consideration, the covariance is a measure of the common variability of two random variables. From this definition of covariance it follows that the covariance of a random variable with itself is equal to the variance of this random variable. In the case of a real random vector , the variance can be generalized to the variance-covariance matrix .

Introduction to the problem

As the starting point for the construction of the variance, one considers any variable that is dependent on chance and can therefore assume different values. This quantity, which is referred to below as , follows a certain distribution . The expected value of this quantity is with ${\displaystyle X}$

${\displaystyle \mu :=\mathbb {E} (X)}$

abbreviated. The expected value indicates which value the random variable assumes on average. It can be interpreted as the focus of the distribution (see also section Interpretation ) and reflects its position. In order to adequately characterize a distribution, however, a quantity is missing that provides information as a key figure about the strength of the spread of a distribution around its center of gravity. This quantity should always be greater than zero, since negative scatter cannot be meaningfully interpreted. A first obvious approach would be to use the mean absolute deviation of the random variable from its expected value: ${\displaystyle X}$

${\displaystyle \mathbb {E} \left(|X-\mu |\right)}$.

Since the absolute value function used in the definition of the mean absolute deviation can not be differentiated everywhere and otherwise sums of squares are usually used in statistics , it makes sense to use the mean square deviation , i.e. the variance , instead of the mean absolute deviation .

definition

Let be a probability space and a random variable on this space. The variance is defined as the expected quadratic deviation of this random variable from its expected value , if this exists: ${\displaystyle (\Omega ,\Sigma ,P)}$ ${\displaystyle X}$ ${\displaystyle \mathbb {E} (X)=\mu }$

${\displaystyle \operatorname {Var} (X):=\mathbb {E} \left((X-\mu )^{2}\right)=\int _{\Omega }(X-\mu )^{2}\,\mathrm {d} P.}$

Explanation

If the variance exists, then applies . However, the variance can also assume the same value , as is the case with the Lévy distribution . ${\displaystyle \operatorname {Var} (X)\geq 0}$ ${\displaystyle \operatorname {Var} (X)=\infty }$

If we consider the centered random variable , the variance is its second moment . If a random variable can be integrated quadratically , that is , because of the shift theorem, its variance is finite and so is the expectation: ${\displaystyle Z:=X-\mu }$ ${\displaystyle \mathbb {E} (Z^{2})}$ ${\displaystyle \mathbb {E} (X^{2})<\infty }$

${\displaystyle |X|\leq X^{2}+1\implies \mathbb {E} (|X|)\leq \mathbb {E} (X^{2})+1<\infty }$.

The variance can be understood as a functional of the space of all probability distributions : ${\displaystyle \chi }$

${\displaystyle \operatorname {Var} [\cdot ]:\chi \to \mathbb {R} _{+}\cup \{\infty \}}$

One distribution for which the variance does not exist is the Cauchy distribution .

notation

Since the variance is a functional , it is often written with square brackets like the expected value (especially in Anglophone literature) . The variance is also noted as or . If there is no danger of confusion, it is simply noted as (read: sigma square ). Since the variance, especially in older literature as dispersion or scattering was called, is also often the notation . ${\displaystyle \operatorname {Var} \left[X\right]}$ ${\displaystyle \operatorname {V} (X)}$ ${\displaystyle \sigma _{X}^{2}}$ ${\displaystyle \sigma ^{2}}$ ${\displaystyle D^{2}(X)}$

The notation with the square of the Greek letter sigma comes from the fact that the calculation of the variance of the density function of a normal distribution corresponds exactly to the parameter of the normal distribution. Since the normal distribution plays a very important role in stochastics, the variance is generally noted as well (see also section Variances of Special Distributions ). Furthermore, in statistics and especially in regression analysis, the symbol is used to identify the true unknown variance of the disturbance variables . ${\displaystyle \sigma }$ ${\displaystyle \sigma ^{2}}$ ${\displaystyle \sigma ^{2}}$ ${\displaystyle \sigma ^{2}}$

Variance in discrete random variables

A random variable with a finite or countably infinite range of values is called discrete . Your variance is then calculated as the weighted sum of the squared deviations (from the expected value): ${\displaystyle X}$ ${\displaystyle {\mathcal {T}}=\{x_{1},x_{2},\dotsc ,x_{k},\dotsc \}}$

${\displaystyle \sigma ^{2}=(x_{1}-\mu )^{2}p_{1}+(x_{2}-\mu )^{2}p_{2}+\ldots +(x_{k}-\mu )^{2}p_{k}+\ldots =\sum _{i\geq 1}(x_{i}-\mu )^{2}p_{i}}$.

Here is the probability that it will take the value . In the above sum, every possible expression is weighted with the probability of its occurrence . In the case of discrete random variables, the variance is therefore a weighted sum with the weights . The expected value of a discrete random variable also represents a weighted sum, which by ${\displaystyle p_{i}=P(X=x_{i})}$ ${\displaystyle X}$ ${\displaystyle x_{i}}$ ${\displaystyle (x_{i}-\mu )^{2}}$ ${\displaystyle p_{i}}$ ${\displaystyle p_{i}\;(i=1,\ldots ,n)}$ ${\displaystyle X}$

${\displaystyle \mu =x_{1}p_{1}+x_{2}p_{2}+\ldots +x_{k}p_{k}+\ldots =\sum _{i\geq 1}x_{i}p_{i}}$

given is. The sums each extend over all values ​​that this random variable can assume. In the case of a countably infinite range of values, there is an infinite sum . In words, the variance is calculated, in the discrete case, as the sum of the products of the probabilities of the realizations of the random variables with the respective squared deviation. ${\displaystyle X}$

Variance in continuous random variables

A random variable is called continuous if its range of values ​​is an uncountable set. If the random variable is absolutely continuous , then as a consequence of the Radon-Nikodým theorem there is a probability density function (in short: density ) . In the case of a real-valued random variables, which makes distribution function , representing the following as an integral: ${\displaystyle X}$ ${\displaystyle f_{X}(x)}$ ${\displaystyle F(t)=P(X\leq t)}$ ${\displaystyle t\in \mathbb {R} }$

${\displaystyle F(t)=\int _{-\infty }^{t}f(x)\,\mathrm {d} x}$

The following applies to the variance of a real-valued random variable with density ${\displaystyle X}$ ${\displaystyle f(x)}$

${\displaystyle \operatorname {Var} (X)=\int _{-\infty }^{\infty }(x-\mathbb {E} [X])^{2}f(x)\,\mathrm {d} x\quad }$, where its expected value is given by . ${\displaystyle \mathbb {E} [X]=\int _{-\infty }^{\infty }xf(x)\,\mathrm {d} x}$

If a density exists, the variance is calculated as the integral over the product of the squared deviation and the density function of the distribution. It is therefore integrated over the space of all possible characteristics (possible value of a statistical feature).

story

Karl Pearson

Ronald Fisher (1913)

The concept of variance goes back to Carl Friedrich Gauß . Gauss introduced the mean square error to show how much a point estimator spreads around the value to be estimated. This idea was adopted from Karl Pearson , the founder of biometrics . For the same idea, he replaced the Gaussian term mean error with his term standard deviation . He then uses this in his lectures. The use of the Greek letter sigma standard deviation was of Pearson, the first time in 1894 in his series of eighteen works entitled Mathematical Contributions to the theory of evolution : (original title Contributions to the Mathematical Theory of Evolution introduced). He wrote there: "[...] then its standard deviation (error of the mean square)". In 1901, Pearson founded Biometrika , which became an important foundation for the Anglo-Saxon school of statistics. ${\displaystyle \sigma }$

The term "variance" was introduced by statistician Ronald Fisher in his 1918 essay entitled The Correlation between Relatives in the Assumption of Mendelian Inheritance (Original title: The Correlation between Relatives on the Supposition of Mendelian Inheritance ). Ronald Fisher writes:

“The large body of statistics available tells us that the deviations of a human measurement from its mean follow the law of normal distribution of disturbance very closely and, consequently, that variability can be measured uniformly by the standard deviation, which is the square root of the mean square Error. If there are two independent causes of variability that are able to produce the standard deviations and in an otherwise uniform population distribution, the distribution is determined to have a standard deviation of, when both causes interact together . It is therefore desirable to analyze the causes of the variability in order to deal with the square of the standard deviation as a measure of the variability. We should call this quantity the variance [...] " ${\displaystyle \sigma _{1}}$ ${\displaystyle \sigma _{2}}$ ${\displaystyle {\sqrt {\sigma _{1}^{2}+\sigma _{2}^{2}}}}$

- The correlation between relatives in the assumption of Mendelian inheritance

Fisher did not introduce a new symbol, just used it to notate the variance. In the following years he developed a genetic model that shows that a continuous variation between phenotypic traits , measured by biostatisticians , can be generated by the combined action of many discrete genes and is thus the result of Mendelian inheritance . Building on these results, Fisher then formulated his fundamental theorem of natural selection , which describes the laws of population genetics for increasing the fitness of organisms. Together with Pearson he developed a. a. the basics of experimental design ( The Design of Experiments appeared in 1935 ) and analysis of variance . Furthermore, the majority of biometric methods can be traced back to Pearson and Fisher, on the basis of which Jerzy Neyman and Egon Pearson developed the general test theory in the 1930s . ${\displaystyle \sigma ^{2}}$

Parameter of a probability distribution

→ Main article : probability distribution

Every probability distribution or random variable can be described by so-called characteristic quantities (also called parameters) that characterize this distribution. The variance and the expected value are the most important parameters of a probability distribution. They are shown in a random variable as additional information as follows: . In words: The random variable follows a (not specified here) distribution with expected value and variance . In the event that the random variable of a special distribution follows, as a standard normal distribution , this is as listed follows: . The expectation of is therefore zero and the variance is one. In addition to the moments, other important parameters of a probability distribution are, for example, the median , mode or quantile . In descriptive statistics, the parameters of a probability distribution correspond to the parameters of a frequency distribution . ${\displaystyle X\;\sim \;(\mu ,\sigma ^{2})}$ ${\displaystyle X}$ ${\displaystyle \mu }$ ${\displaystyle \sigma ^{2}}$ ${\displaystyle X\;\sim \;{\mathcal {N}}(0,1)}$ ${\displaystyle X}$

Chebyshev's inequality

→ Main article : Chebyshev's inequality

With the help of Chebyshev's inequality, using the existing first two moments, the probability of the random variable assuming values ​​in certain intervals of the real number line can be estimated without knowing the distribution of . For a random variable with expected value and variance it reads : ${\displaystyle X}$ ${\displaystyle X}$ ${\displaystyle X}$ ${\displaystyle \mu }$ ${\displaystyle \sigma ^{2}}$

${\displaystyle P\left(\left|X-\mu \right|\geq k\right)\leq {\frac {\sigma ^{2}}{k^{2}}}\quad ,k>0}$.

Chebyshev's inequality applies to all symmetrical and skewed distributions. So it does not require any particular form of distribution. A disadvantage of Chebyshev's inequality is that it only provides a rough estimate.

interpretation

Physical interpretation

In addition to the expected value, the variance is the second important parameter of the distribution of a real random variable. The -th central moment of is . If so , then the second order central moment is called the variance of the distribution of . The term moment originally comes from physics . If you interpret the possible values ​​as mass points with the masses on the real number line (assumed to be weightless), then you get a physical interpretation of the expected value: The first moment, the expected value, then represents the physical center of gravity or center of mass of the resulting body. The variance can then be interpreted as the moment of inertia of the mass system with respect to the axis of rotation around the center of gravity. In contrast to the expected value, which balances the probability measure, the variance is a measure of the spread of the probability measure around its expected value. ${\displaystyle r}$ ${\displaystyle X}$ ${\displaystyle \mu _{r}=\mathbb {E} \left((X-\mu )^{r}\right)}$ ${\displaystyle r=2}$ ${\displaystyle \mu _{2}=\mathbb {E} \left((X-\mu )^{2}\right)}$ ${\displaystyle X}$

Interpretation as a distance

The interpretation of the variance of a random variable as the mean squared distance can be explained as follows: The distance between two points and on the real number line is given by . If you now define that one point is the random variable and the other , then it holds and the distance squared is . Consequently, it is interpreted as the mean squared distance between the realization of the random variable and the expected value if the random experiment is repeated an infinite number of times. ${\displaystyle x_{1}}$ ${\displaystyle x_{2}}$ ${\displaystyle d={\sqrt {(x_{1}-x_{2})^{2}}}}$ ${\displaystyle X}$ ${\displaystyle \mu =\mathbb {E} (X)}$ ${\displaystyle d={\sqrt {(X-\mu )^{2}}}}$ ${\displaystyle (X-\mu )^{2}}$ ${\displaystyle \mathbb {E} ((X-\mu )^{2})}$ ${\displaystyle X}$ ${\displaystyle \mathbb {E} (X)}$

Interpretation as a measure of determinism

Density functions of normally distributed random variables with different expected values ​​and variances. It can be seen that the expected value reflects the position and variance the width of the density function. The red curve shows the standard normal distribution with expected value zero and variance one. ${\displaystyle {\mathcal {N}}(0,1)}$

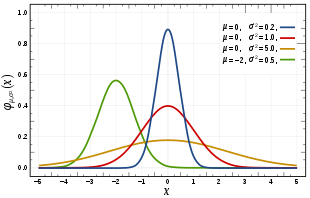
The variance also describes the breadth of a probability function and therefore how “stochastic” or how “deterministic” a phenomenon is. With a large variance, the situation is more likely to be stochastic, and with a small variance, the situation is more deterministic. In the special case of a variance of zero, the situation is completely deterministic. The variance is zero if and only if the random variable assumes only one specific value, namely the expected value, with one hundred percent probability; if so . Such a “random variable” is a constant, that is, completely deterministic. Since a random variable with this property applies to all , its distribution is called “degenerate”. ${\displaystyle X}$ ${\displaystyle P(X=\mu )=1}$ ${\displaystyle P(X=x)=0}$ ${\displaystyle x\neq \mu }$

In contrast to discrete random variables, continuous random variables always apply to each . In the continuous case, the variance describes the width of a density function. The width, in turn, is a measure of the uncertainty associated with a random variable. The narrower the density function, the more accurately the value of can be predicted. ${\displaystyle P(X=x)=0}$ ${\displaystyle x\in \mathbb {R} }$ ${\displaystyle X}$

Calculation rules and properties

The variance has a wealth of useful properties that make the variance the most important measure of dispersion:

Displacement set

The displacement law is the stochastic analogue of Steiner's theorem for calculating moments of inertia . It applies with and for anything real : ${\displaystyle \mathbb {E} (X)=\mu }$ ${\displaystyle a}$

${\displaystyle \mathbb {E} \left((X-a)^{2}\right)=\operatorname {Var} (X)+(\mu -a)^{2}}$,

d. H. the mean square deviation from or (physical: the moment of inertia with respect to the axis ) is equal to the variance (physical: equal to the moment of inertia with respect to the axis through the center of gravity ) plus the square of the displacement . ${\displaystyle X}$ ${\displaystyle a}$ ${\displaystyle a}$ ${\displaystyle \mu }$ ${\displaystyle \mu -a}$

Proof . The middle term results by exploiting the linearity of expectation: . This proves the above formula. ${\displaystyle \mathbb {E} \left((X-a)^{2}\right)=\mathbb {E} \left((X-\mu +\mu -a)^{2}\right)=\operatorname {Var} (X)+2\mathbb {E} \left((X-\mu )(\mu -a)\right)+(\mu -a)^{2}}$ ${\displaystyle 2\mathbb {E} \left((X-\mu )(\mu -a)\right)=2(\mu -a)(\mathbb {E} \left(X\right)-\mu )=0}$

From the displacement theorem, we also get for any real thing : ${\displaystyle a}$

${\displaystyle \operatorname {Var} (X)\leq \mathbb {E} \left((X-a)^{2}\right)\quad }$or . ${\displaystyle \quad \operatorname {Var} (X)=\min _{a\in R}\mathbb {E} \left((X-a)^{2}\right)}$

(see also the Fréchet principle )

For is the best-known variant of the displacement theorem ${\displaystyle a=0}$

${\displaystyle \operatorname {Var} (X)=\mathbb {E} \left(X^{2}\right)-\mathbb {E} \left(X\right)^{2}=\mathbb {E} \left(X^{2}\right)-\mu ^{2}}$.

The variance as a central moment related to the expected value (the “center”) can also be expressed as a non-central moment.

Because of the nonnegativity condition of the variance, it follows from the shift theorem that ; thus is . This result is a special case of those inequality for expectation values. The shift theorem accelerates the calculation of the variance, since the required expected value of can be formed together with , while otherwise it must already be known - specifically for discrete or continuous random variables it delivers: ${\displaystyle \mathbb {E} \left(X^{2}\right)-\left(\mathbb {E} (X)\right)^{2}\geq 0}$ ${\displaystyle \mathbb {E} \left(X^{2}\right)\geq \left(\mathbb {E} (X)\right)^{2}}$ ${\displaystyle X^{2}}$ ${\displaystyle \mu }$ ${\displaystyle \mu }$

If discreet ${\displaystyle X}$	If steady ${\displaystyle X}$
${\displaystyle \sigma ^{2}=\left(\sum _{i\geq 1}x_{i}^{2}p_{i}\right)-\left(\sum _{i\geq 1}x_{i}p_{i}\right)^{2}}$	${\displaystyle \sigma ^{2}=\int _{-\infty }^{\infty }x^{2}f(x)\,\mathrm {d} x-\left(\int _{-\infty }^{\infty }xf(x)\,\mathrm {d} x\right)^{2}}$

Linear transformation

The following applies to two constants : ${\displaystyle a,b\in \mathbb {R} }$

• The variance of a constant is zero because constants are not random by definition and therefore do not scatter: ; ${\displaystyle \operatorname {Var} (a)=0}$ ${\displaystyle \operatorname {Var} (b)=0}$
• Translation invariance : The following applies to additive constants . This means that a “shift in the random variables” by a constant amount has no effect on their dispersion. ${\displaystyle \operatorname {Var} (X+b)=\mathbb {E} \left((X+b-\mu -b)^{2}\right)=\operatorname {Var} (X)}$
• In contrast to additive constants, multiplicative constants have an effect on the scaling of the variance. With multiplicative constants, the variance is scaled with the squared of the constants , i.e.,. This can be shown as follows: ${\displaystyle a^{2}}$

${\displaystyle \operatorname {Var} (aX)=\mathbb {E} \left((aX-a\mu )^{2}\right)=\mathbb {E} \left(a^{2}(X-\mu )^{2}\right)=a^{2}\operatorname {Var} (X)}$.

Here, the property of linearity of the expected value was used. In summary, the formation of the variance of a linear transformed random variable results in : ${\displaystyle Y=aX+b}$

${\displaystyle \operatorname {Var} (Y)=\operatorname {Var} (aX+b)=a^{2}\operatorname {Var} (X)}$.

In particular for follows , that is, the sign of the variance does not change if the sign of the random variable changes. ${\displaystyle a=-1}$ ${\displaystyle \operatorname {Var} (-X)=\operatorname {Var} (X)}$

Every random variable can be converted into a random variable by centering and subsequent normalization , called standardization . This normalization is a linear transformation. The random variable standardized in this way has a variance of and an expected value of . ${\displaystyle Z}$ ${\displaystyle Z}$ ${\displaystyle 1}$ ${\displaystyle 0}$

Relationship to the standard deviation

The variance of a random variable is always given in square units. This is problematic because squared units that come about this way - such as - do not offer any meaningful interpretation; the interpretation as area measure is inadmissible in the present example. In order to get the same unit as the random variable, instead of the variance i. d. Usually the standard deviation is used. It has the same unit as the random variable itself and thus measures, figuratively speaking, "with the same measure". ${\displaystyle {\text{cm}}^{2}}$

The standard deviation is the positive square root of the variance

${\displaystyle \operatorname {SD} (X):=+{\sqrt {\operatorname {Var} (X)}}=+{\sqrt {\mathbb {E} \left((X-\mu )^{2}\right)}}}$.

It is noted as (occasionally as ) ,, or simply as ( Sigma ). Furthermore, the standard deviation is suitable for quantifying the uncertainty in decisions under risk because, unlike the variance, it meets the requirements for a risk measure. ${\displaystyle \operatorname {SD} (X)}$ ${\displaystyle D(X)}$ ${\displaystyle \sigma _{X}}$ ${\displaystyle \sigma }$

With some probability distributions, especially the normal distribution , probabilities can be calculated directly from the standard deviation. With the normal distribution, approx. 68% of the values ​​are always in the interval of the width of two standard deviations from the expected value. An example of this is body size : it is approximately normally distributed for a nation and gender , so that e.g. For example, in Germany in 2006 approx. 68% of all men were between 171 and 186 cm tall (approx. , Ie “expected value plus / minus standard deviation”). ${\displaystyle 178{,}3\pm 7{,}3\;{\text{cm}}}$

For the standard deviation is true of any constant , . In contrast to the variance calculation rule applies to the standard deviation of linear transformations, that is, the standard deviation is in contrast to the variance not with the square scaled the constant. In particular, for , . ${\displaystyle c}$ ${\displaystyle \operatorname {SD} (c)=0}$ ${\displaystyle \operatorname {SD} (aX+b)=|a|\operatorname {SD} (X)}$ ${\displaystyle a,b\in \mathbb {R} }$ ${\displaystyle a^{2}}$ ${\displaystyle a>0}$ ${\displaystyle \operatorname {SD} (aX+b)=a\cdot \operatorname {SD} (X)}$

Relationship to covariance

→ Main article : Covariance (stochastics)

In contrast to the variance, which only measures the variability of the random variable under consideration, the covariance measures the joint variability of two random variables. The variance is therefore the covariance of a random variable with itself . This relationship follows directly from the definition of variance and covariance. The covariance between and is also abbreviated with . In addition, since the covariance is a positive semidefinite bilinear form , the Cauchy-Schwarz inequality applies : ${\displaystyle \operatorname {Cov} (X,X)=\operatorname {Var} (X)}$ ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle \sigma _{XY}}$

${\displaystyle (\operatorname {Cov} (X,Y))^{2}\leq \operatorname {Var} (X)\operatorname {Var} (Y)}$.

This inequality is one of the most important in mathematics and is mainly used in linear algebra .

Sums and products

The following generally applies to the variance of any sum of random variables : ${\displaystyle X=a_{1}X_{1}+\dotsb +a_{n}X_{n}}$

${\displaystyle {\begin{aligned}\operatorname {Var} \left(X\right)&=a_{1}^{2}\operatorname {Var} \left(X_{1}\right)+\dotsb +a_{n}^{2}\operatorname {Var} \left(X_{n}\right)+2a_{1}a_{2}\operatorname {Cov} \left(X_{1},X_{2}\right)+2a_{1}a_{3}\operatorname {Cov} \left(X_{1},X_{3}\right)+\dotsb \\&=\sum \nolimits _{i=1}^{n}a_{i}^{2}\operatorname {Var} (X_{i})+2\sum \nolimits _{i<j}a_{i}a_{j}\operatorname {Cov} (X_{i},X_{j})\\\end{aligned}}}$.

Here denotes the covariance of the random variables and and the property was used. If the behavior of the variance in linear transformations is taken into account, then the following applies to the variance of the linear combination , or the weighted sum, of two random variables: ${\displaystyle \operatorname {Cov} \left(X_{i},X_{j}\right)}$ ${\displaystyle X_{i}}$ ${\displaystyle X_{j}}$ ${\displaystyle \operatorname {Cov} \left(X_{i},X_{i}\right)=\operatorname {Var} \left(X_{i}\right)}$

${\displaystyle \operatorname {Var} (aX+bY)=a^{2}\operatorname {Var} (X)+b^{2}\operatorname {Var} (Y)+2ab\operatorname {Cov} (X,Y)}$.

Especially for two random variables , and results for example ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle a=b=1}$

${\displaystyle \operatorname {Var} (X+Y)=\operatorname {Var} (X)+\operatorname {Var} (Y)+2\operatorname {Cov} (X,Y)}$.

This means that the variability of the sum of two random variables results in the sum of the individual variabilities and twice the common variability of the two random variables.

Another reason why variance is preferred over other measures of dispersion is the useful property that the variance of the sum of independent random variables is equal to the sum of the variances:

${\displaystyle \operatorname {Var} (X\pm Y)=\operatorname {Var} (X)+\operatorname {Var} (Y)}$.

This results from the fact that the following applies to independent random variables . This formula can also be generalized: If pairwise uncorrelated random variables are (that is, their covariances are all zero), then applies ${\displaystyle \operatorname {Cov} (X,Y)=0}$ ${\displaystyle \{X_{1},\dotsc ,X_{n}\}}$

${\displaystyle \operatorname {Var} \left(X_{1}+\dotsb +X_{n}\right)=\operatorname {Var} (X_{1})+\dotsb +\operatorname {Var} (X_{n})}$,

or more generally with any constants ${\displaystyle a_{1},\dotsc ,a_{n}}$

${\displaystyle {\begin{aligned}\operatorname {Var} \left(a_{1}X_{1}+\dotsb +a_{n}X_{n}\right)=a_{1}^{2}\operatorname {Var} \left(X_{1}\right)+\dotsb +a_{n}^{2}\operatorname {Var} \left(X_{n}\right)\end{aligned}}}$.

This result was discovered in 1853 by the French mathematician Irénée-Jules Bienaymé and is therefore also known as the Bienaymé equation . It is especially true if the random variables are independent , because independence follows uncorrelation. If all random variables have the same variance , this means for the variance formation of the sample mean: ${\displaystyle \sigma ^{2}}$

${\displaystyle \operatorname {Var} \left({\overline {X}}\right)=\operatorname {Var} \left({\frac {1}{n}}\sum _{i=1}^{n}X_{i}\right)={\frac {1}{n^{2}}}\sum _{i=1}^{n}\operatorname {Var} \left(X_{i}\right)={\frac {\sigma ^{2}}{n}}}$.

It can be seen that the variance of the sample mean decreases as the sample size increases. This formula for the variance of the sample mean is used in defining the standard error of the sample mean that is used in the central limit theorem. ${\displaystyle n}$

If two random variables and are independent, then the variance of their product is given by ${\displaystyle X}$ ${\displaystyle Y}$

${\displaystyle {\begin{aligned}\operatorname {Var} (XY)&=(\mathbb {E} (X))^{2}\operatorname {Var} (Y)+(\mathbb {E} (Y))^{2}\operatorname {Var} (X)+\operatorname {Var} (X)\operatorname {Var} (Y)\end{aligned}}}$.

Compound random variable

Is a composite random variable , i. H. are independent random variables, are identically distributed and is on defined, it can be represented as . If the second moments of exist , the following applies to the composite random variable: ${\displaystyle Y}$ ${\displaystyle N,X_{1},X_{2},\dotsc }$ ${\displaystyle X_{i}}$ ${\displaystyle N}$ ${\displaystyle \mathbb {N} _{0}}$ ${\displaystyle Y}$ ${\displaystyle Y:=\sum \nolimits _{i=1}^{N}X_{i}}$ ${\displaystyle N,X_{1},X_{2},\dotsc }$

${\displaystyle \operatorname {Var} (Y)=\operatorname {Var} (N)\left(\mathbb {E} \left(X_{1}\right)\right)^{2}+\mathbb {E} (N)\operatorname {Var} \left(X_{1}\right)}$.

This statement is also known as the Blackwell-Girshick equation and is used e.g. B. used in insurance mathematics.

Moment generating and cumulative generating function

With the help of the torque-generating function , moments such as the variance can often be calculated more easily. The moment generating function is defined as the expected value of the function . Since the relationship for the moment generating function ${\displaystyle e^{tX}}$ ${\displaystyle \mathbb {E} \left(e^{tX}\right)}$

${\displaystyle M_{X}^{(n)}(t=0)=\mathbb {E} \left(X^{n}\right)}$

holds, the variance can be calculated using the displacement law in the following way:

${\displaystyle \operatorname {Var} (X)=\mathbb {E} \left(X^{2}\right)-(\mathbb {E} (X))^{2}=M_{X}''(0)-\left(M_{X}'(0)\right)^{2}}$.

Here is the moment generating function and the th derivative of this. The cumulative-generating function of a random variable results from the logarithm of the moment-generating function and is defined as: ${\displaystyle M_{X}}$ ${\displaystyle M_{X}^{(n)}}$ ${\displaystyle n}$

${\displaystyle g_{X}(t):=\ln \mathbb {E} (e^{tX})}$.

If you derive it twice and evaluate it at the point zero, you get the variance . So the second cumulant is the variance. ${\displaystyle g''_{X}(t){\bigg |}_{t=0}=\sigma ^{2}}$

Characteristic and probability-generating function

The variance of a random variable can also be represented with the help of its characteristic function . Because of ${\displaystyle X}$ ${\displaystyle \varphi _{X}(t)=\mathbb {E} \left(e^{\mathrm {i} tX}\right)}$

${\displaystyle \mathbb {E} (X^{k})={\frac {\varphi _{X}^{(k)}(0)}{\mathrm {i} ^{k}}}\;,k=1,2,\dots }$and it follows with the displacement theorem: ${\displaystyle (\mathbb {E} (X))^{2}=\left({\frac {\varphi _{X}'(0)}{\mathrm {i} }}\right)^{2}}$

${\displaystyle \operatorname {Var} (X)=\mathbb {E} (X^{2})-(\mathbb {E} (X))^{2}={\frac {\varphi _{X}''(0)}{\mathrm {i} ^{2}}}-\left({\frac {\varphi _{X}'(0)}{\mathrm {i} }}\right)^{2}}$.

The variance for discrete can also be calculated with the probability-generating function , which is related to the characteristic function . It then applies to the variance if the left-hand limit value exists. ${\displaystyle m_{X}(t)=\mathbb {E} (t^{X})}$ ${\displaystyle X}$ ${\displaystyle \sigma ^{2}=\lim _{t\uparrow 1}\left(m_{X}''(t)+m_{X}'(t)-m_{X}'(t)^{2}\right)}$

Variance as the mean square deviation from the mean

In the case of a discrete random variable with a countably finite carrier , the variance of the random variable results as ${\displaystyle X}$ ${\displaystyle {\mathcal {T}}=\{x_{1},x_{2},\dotsc ,x_{n}\}\subset \mathbb {R} }$ ${\displaystyle \operatorname {Var} (X)}$

${\displaystyle \operatorname {Var} (X)=p_{1}(x_{1}-\mu )^{2}+p_{2}(x_{2}-\mu )^{2}+\dotsb +p_{n}\left(x_{n}-\mu \right)^{2}}$.

Here is the probability that it will take the value . This variance can be interpreted as a weighted sum of the values weighted with the probabilities . ${\displaystyle p_{i}=P\left(X=x_{i}\right)}$ ${\displaystyle X}$ ${\displaystyle x_{i}}$ ${\displaystyle \left(x_{1}-\mu \right)^{2},\left(x_{2}-\mu \right)^{2},\dotsc ,\left(x_{n}-\mu \right)^{2}}$ ${\displaystyle p_{1},p_{2},\dotsc ,p_{n}}$

If is evenly distributed to ( ), the following applies to the expected value: it is equal to the arithmetic mean (see Weighted arithmetic mean as expected value ): ${\displaystyle X}$ ${\displaystyle \{x_{1},x_{2},\dotsc ,x_{n}\}\subset \mathbb {R} }$ ${\displaystyle p_{1}=p_{2}=\dotsb =p_{n}=1/n}$

${\displaystyle \mu =\operatorname {E} (X)={\frac {1}{n}}\left(x_{1}+x_{2}+\dotsb +x_{n}\right)={\frac {1}{n}}\sum _{i=1}^{n}{x_{i}}={\overline {x}}}$

Consequently, the variance becomes the arithmetic mean of the values : ${\displaystyle \operatorname {Var} (X)=p_{1}\left(x_{1}-\mu \right)^{2}+p_{2}\left(x_{2}-\mu \right)^{2}+\dotsb +p_{n}\left(x_{n}-\mu \right)^{2}}$ ${\displaystyle \left(x_{i}-{\overline {x}}\right)^{2}}$

${\displaystyle \sigma ^{2}=\operatorname {Var} (X)={\frac {1}{n}}\left(\left(x_{1}-{\overline {x}}\right)^{2}+\left(x_{2}-{\overline {x}}\right)^{2}+\dotsb +\left(x_{n}-{\overline {x}}\right)^{2}\right)={\frac {1}{n}}\sum _{i=1}^{n}{\left(x_{i}-{\overline {x}}\right)^{2}}=s^{2}}$.

In other words, with uniform distribution, the variance is precisely the mean square deviation from the mean or the sample variance . ${\displaystyle s^{2}}$

Variances of special distributions

In stochastics there are a large number of distributions , which mostly show a different variance and are often related to one another . The variance of the normal distribution is of great importance, since the normal distribution has an extraordinary position in statistics. The special importance of the normal distribution is based, among other things, on the central limit theorem , according to which distributions that arise from the superposition of a large number of independent influences are approximately normally distributed under weak conditions. A selection of important variances is summarized in the following table:

distribution	Constant / discreet	Probability function	Variance
Normal distribution	Steady	${\displaystyle f(x\mid \mu ,\sigma ^{2})={\frac {1}{\sqrt {2\pi \sigma ^{2}}}}\operatorname {exp} \left\{-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}\right\}}$	${\displaystyle \sigma ^{2}}$
Cauchy distribution	Steady	${\displaystyle f(x)={\frac {1}{\pi }}\cdot {\frac {s}{s^{2}+(x-t)^{2}}}}$	does not exist
Bernoulli distribution	Discreet	${\displaystyle f(x\mid p)={\begin{cases}p^{x}(1-p)^{1-x}&{\text{falls}}\quad x=0,1\\0&{\text{sonst.}}\end{cases}}}$	${\displaystyle p(1-p)}$
Binomial distribution	Discreet	${\displaystyle f(x\mid n,p)={\begin{cases}{\binom {n}{x}}p^{x}(1-p)^{n-x}&{\text{falls}}\quad x=0,1,\dots ,n\\0&{\text{sonst.}}\end{cases}}}$	${\displaystyle np(1-p)}$
Constant equal distribution	Steady	${\displaystyle f(x)={\begin{cases}{\frac {1}{b-a}}&a\leq x\leq b\\0&{\text{sonst.}}\end{cases}}}$	${\displaystyle {\frac {1}{12}}(b-a)^{2}}$
Poisson distribution	Discreet	${\displaystyle f(x)={\begin{cases}{\frac {\lambda ^{x}}{x!}}\,\mathrm {e} ^{-\lambda }&{\text{falls}}\quad x\in \{0,1,\dots \}\\0&{\text{sonst.}}\end{cases}}}$	${\displaystyle \lambda }$

Examples

Calculation for discrete random variables

A discrete random variable is given which assumes the values , and with the probabilities , and . These values ​​can be summarized in the following table ${\displaystyle X}$ ${\displaystyle -1}$ ${\displaystyle 1}$ ${\displaystyle 2}$ ${\displaystyle 0{,}5}$ ${\displaystyle 0{,}3}$ ${\displaystyle 0{,}2}$

${\displaystyle X=x_{i}}$	${\displaystyle -1}$	${\displaystyle 1}$	${\displaystyle 2}$
${\displaystyle P(X=x_{i})=p_{i}}$	${\displaystyle 0{,}5}$	${\displaystyle 0{,}3}$	${\displaystyle 0{,}2}$	${\displaystyle \sum _{i}p_{i}=1}$

The expected value is according to the above definition

${\displaystyle {\color {BrickRed}\mu }=\sum _{i=1}^{3}x_{i}p_{i}=-1\cdot 0{,}5+1\cdot 0{,}3+2\cdot 0{,}2={\color {BrickRed}0{,}2}}$.

The variance is therefore given by

${\displaystyle \sigma ^{2}=\sum _{i=1}^{3}(x_{i}-{\color {BrickRed}\mu })^{2}p_{i}=(-1-{\color {BrickRed}0{,}2})^{2}\cdot 0{,}5+(1-{\color {BrickRed}0{,}2})^{2}\cdot 0{,}3+(2-{\color {BrickRed}0{,}2})^{2}\cdot 0{,}2=1{,}56}$.

The same value for the variance is also obtained with the displacement theorem:

${\displaystyle \sigma ^{2}=\left(\sum _{i=1}^{3}x_{i}^{2}p_{i}\right)-\left(\sum _{i=1}^{3}x_{i}p_{i}\right)^{2}=(-1)^{2}\cdot 0{,}5+1^{2}\cdot 0{,}3+2^{2}\cdot 0{,}2-{\color {BrickRed}0{,}2}^{2}=1{,}56}$.

The standard deviation thus results:

${\displaystyle \sigma ={\sqrt {\sigma ^{2}}}={\sqrt {1{,}56}}\approx 1{,}249}$.

Calculation for continuous random variables

The density function is a continuous random variable

${\displaystyle f(x)={\begin{cases}{\frac {1}{x}}&{\text{falls}}\quad 1\leq x\leq e\\0&{\text{sonst.}}\end{cases}}}$,

with the expected value of ${\displaystyle X}$

${\displaystyle {\color {BrickRed}\mu }=\int _{1}^{e}x\cdot {\frac {1}{x}}\,\mathrm {d} x=\color {BrickRed}{e-1}}$

and the expected value of ${\displaystyle X^{2}}$

${\displaystyle \mathbb {E} {\bigl (}X^{2}{\bigr )}=\int _{-\infty }^{\infty }x^{2}\cdot f(x)\,\mathrm {d} x=\int _{1}^{e}x^{2}\cdot {\frac {1}{x}}\,\mathrm {d} x=\left[{\frac {x^{2}}{2}}\right]_{1}^{e}={\frac {e^{2}}{2}}-{\frac {1}{2}}}$.

The variance of this density function is calculated with the help of the displacement law as follows:

${\displaystyle \sigma ^{2}=\int _{-\infty }^{\infty }x^{2}f(x)\,\mathrm {d} x-{\color {BrickRed}\mu }^{2}={\frac {e^{2}}{2}}-{\frac {1}{2}}-{\color {BrickRed}(e-1)}^{2}\approx 0{,}242}$.

Sample variance as an estimate of the variance

→ Main article : Sample variance (estimator)

Let be real, independently and identically distributed random variables with the expected value and the finite variance . An estimator for the expected value is the sample mean , since according to the law of large numbers : ${\displaystyle X_{1},\dots ,X_{n}}$ ${\displaystyle \mathbb {E} (X_{i})=b}$ ${\displaystyle \sigma ^{2}=\operatorname {Var} (X_{i})}$ ${\displaystyle b}$ ${\displaystyle {\overline {X}}_{n}}$

${\displaystyle {\overline {X}}_{n}\;{\overset {p}{\longrightarrow }}\;b}$.

In the following, an estimator for the variance is sought. Starting from one defines the random variables . These are distributed independently and identically with the expected value . If it is possible to integrate quadratically, then the weak law of large numbers is applicable, and we have: ${\displaystyle \sigma ^{2}}$ ${\displaystyle X_{1},\dots ,X_{n}}$ ${\displaystyle Y_{i}:=(X_{i}-b)^{2},\quad i=1,\dots ,n}$ ${\displaystyle \mathbb {E} (Y_{i})=\mathbb {E} (X_{i}-b)^{2}=\sigma ^{2}}$ ${\displaystyle Y}$

${\displaystyle {\overline {Y}}_{n}={\frac {1}{n}}\sum _{i=1}^{n}(X_{i}-b)^{2}\;{\overset {p}{\longrightarrow }}\;\sigma ^{2}}$.

Now, if you by replacing, this provides the so-called sample variance. Because of this, as shown above, represents the sample variance ${\displaystyle b}$ ${\displaystyle {\overline {X}}_{n}}$

${\displaystyle {\widetilde {S}}_{n}={\frac {1}{n}}\sum _{i=1}^{n}(X_{i}-{\overline {X}}_{n})^{2}}$

represents an inductive equivalent of the variance in the stochastic sense.

Conditional variance

→ Main article : Conditional variance

Analogous to conditional expected values, conditional variances of conditional distributions can be considered when additional information is available, such as the values ​​of a further random variable . Let and be two real random variables, then is called the variance of which is conditioned on ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle X}$ ${\displaystyle Y=y}$

${\displaystyle \operatorname {Var} (X\mid Y=y)=\mathbb {E} {\bigl (}(X-\mathbb {E} (X\mid y))^{2}\mid y{\bigr )}}$

the conditional variance of given ${\displaystyle X}$ ${\displaystyle Y=y}$ (or variance of conditional on ${\displaystyle X}$ ${\displaystyle Y=y}$ ). In order to differentiate the “ordinary” variance more strongly from the conditional variance , the ordinary variance is also referred to as the unconditional variance . ${\displaystyle \operatorname {Var} (X)}$ ${\displaystyle \operatorname {Var} (X\mid Y=y)}$

Generalizations

Variance-covariance matrix

→ Main article : Covariance matrix

In the case of a real random vector with the associated expectation value vector , the variance or covariance generalizes to the symmetrical variance-covariance matrix (or simply covariance matrix) of the random vector: ${\displaystyle {\boldsymbol {X}}=(X_{1},\dots ,X_{p})^{\top }}$ ${\displaystyle {\boldsymbol {\mu }}=(\mu _{1},\dots ,\mu _{p})^{\top }}$

${\displaystyle \operatorname {Cov} (\mathbf {X} )=\mathbb {E} \left(({\boldsymbol {X}}-{\boldsymbol {\mu }})({\boldsymbol {X}}-{\boldsymbol {\mu }})^{\top }\right)}$.

The entry of the -th row and -th column of the variance-covariance matrix is the covariance of the random variables and the variances are on the diagonal . Since the covariances are a measure of the correlation between random variables and the variances are only a measure of the variability, the variance-covariance matrix contains information about the dispersion and correlations between all of its components. Since the variances and covariances are always non-negative by definition, the same applies to the variance-covariance matrix that it is positive semidefinite . The variance-covariance matrix serves as an efficiency criterion when evaluating estimators . In general, the efficiency of a parameter estimator can be measured by the “size” of its variance-covariance matrix. The following applies: the “smaller” the variance-covariance matrix, the “greater” the efficiency of the estimator. ${\displaystyle i}$ ${\displaystyle j}$ ${\displaystyle \operatorname {Cov} (\mathbf {X} )}$ ${\displaystyle \operatorname {Cov} (X_{i},X_{j}),\;i\neq j}$ ${\displaystyle X_{i}}$ ${\displaystyle X_{j}}$ ${\displaystyle \operatorname {Cov} (X_{i},X_{i})=\operatorname {Var} (X_{i})}$

Matrix notation for the variance of a linear combination

Let it be a column vector of random variables and a column vector consisting of scalars . This means that this is a linear combination of these random variables, where the transpose of denotes. Let be the variance-covariance matrix of . The variance of is then given by: ${\displaystyle {\boldsymbol {X}}}$ ${\displaystyle p}$ ${\displaystyle X_{1},\ldots ,X_{p}}$ ${\displaystyle {\boldsymbol {a}}}$ ${\displaystyle p}$ ${\displaystyle a_{1},\ldots ,a_{p}}$ ${\displaystyle {\boldsymbol {a}}^{\top }{\boldsymbol {X}}}$ ${\displaystyle {\boldsymbol {a}}^{\top }}$ ${\displaystyle {\boldsymbol {a}}}$ ${\displaystyle {\boldsymbol {\Sigma }}_{\boldsymbol {X}}=(\sigma _{ij})}$ ${\displaystyle {\boldsymbol {X}}}$ ${\displaystyle {\boldsymbol {a}}^{\top }{\boldsymbol {X}}}$

${\displaystyle \operatorname {Var} ({\boldsymbol {a}}^{\top }{\boldsymbol {X}})={\boldsymbol {a}}^{\top }{\boldsymbol {\Sigma }}_{\boldsymbol {X}}{\boldsymbol {a}}=\sum _{i=1}^{p}\sum _{j=1}^{p}a_{i}a_{j}\sigma _{ij}}$.

Related measures

If one understands the variance as a measure of the dispersion of the distribution of a random variable, then it is related to the following measures of dispersion:

• Variation coefficient : The variation coefficient as the ratio of standard deviation and expected value and thus a dimensionless measure of dispersion
• Quantile distance : The quantile distance to the parameter indicates how far apart the - and the - quantile are ${\displaystyle p}$ ${\displaystyle p}$ ${\displaystyle (1-p)}$
• Mean absolute deviation : The mean absolute deviation as the first absolute central moment

Web links

Wikibooks: Variance and Standard  Deviation - Learning and Teaching Materials

Commons : standard deviation  - album with pictures, videos and audio files

Commons : Variance  - collection of images, videos and audio files

Wiktionary: Variance  - explanations of meanings, word origins, synonyms, translations

• Eric W. Weisstein : Variance . In: MathWorld (English).
• Detailed calculations for the discrete and continuous case at www.mathebibel.de

literature

• George G. Judge, R. Carter Hill, W. Griffiths, Helmut Lütkepohl , TC Lee. Introduction to the Theory and Practice of Econometrics. John Wiley & Sons, New York, Chichester, Brisbane, Toronto, Singapore, ISBN 978-0-471-62414-1 , second edition 1988
• Ludwig Fahrmeir among others: Statistics: The way to data analysis. 8., revised. and additional edition. Springer-Verlag, 2016, ISBN 978-3-662-50371-3 .

Remarks

1. ↑ For a symmetrical distribution with the center of symmetry applies: . ${\displaystyle x_{0}}$ ${\displaystyle \mu =\mathbb {E} (X)=x_{0}}$
2. ↑ Further advantages of squaring are, on the one hand, that small deviations are weighted less heavily than large deviations, and on the other hand, that the first derivative is a linear function, which is an advantage when considering optimization.
3. ↑ The use of the variance operator emphasizes the calculation operations, and with it the validity of certain calculation operations can be better expressed. ${\displaystyle \operatorname {Var} (\cdot )}$
4. ↑ The term "carrier" and the symbol denote the set of all possible manifestations or realizations of a random variable. ${\displaystyle {\mathcal {T}}}$

Individual evidence

1. ↑ Norbert Henze: Stochastics for Beginners: An Introduction to the Fascinating World of Chance. 2016, p. 160.
2. ↑ Ludwig von Auer : Econometrics. An introduction. Springer, ISBN 978-3-642-40209-8 , 6th through. u. updated edition 2013, p. 28.
3. ↑ Volker Heun: Basic Algorithms: Introduction to the Design and Analysis of Efficient Algorithms. 2nd Edition. 2003, p. 108.
4. ↑ Gerhard Hübner: Stochastics: An application-oriented introduction for computer scientists, engineers and mathematicians. 3rd edition, 2002, p. 103.
5. ↑ Patrick Billingsley: Probability and Measure , 3rd ed., Wiley, 1995, pp. 274ff
6. ^ Otfried Beyer, Horst Hackel: Probability calculation and mathematical statistics. 1976, p. 53.
7. ↑ Brockhaus: Brockhaus, Natural Sciences and Technology - Special Edition. 1989, p. 188.
8. ^ Lothar Papula: Mathematics for engineers and scientists. Volume 3: Vector analysis, probability calculation, mathematical statistics, error and compensation calculation. 1994, p. 338.
9. ^ Ludwig Fahrmeir , Rita artist , Iris Pigeot , and Gerhard Tutz : Statistics. The way to data analysis. 8., revised. and additional edition. Springer Spectrum, Berlin / Heidelberg 2016, ISBN 978-3-662-50371-3 , p. 231.
10. ↑ Von Auer: Econometrics. An introduction. 6th edition. Springer, 2013, ISBN 978-3-642-40209-8 , p. 29.
11. ^ Ludwig Fahrmeir , Rita artist , Iris Pigeot , and Gerhard Tutz : Statistics. The way to data analysis. 8., revised. and additional edition. Springer Spectrum, Berlin / Heidelberg 2016, ISBN 978-3-662-50371-3 , p. 283.
12. ↑ Ronald Aylmer Fisher : The correlation between relatives on the supposition of Mendelian inheritance. , Trans. Roy. Soc. Edinb. 52 : 399-433, 1918.
13. ^ Lothar Sachs : Statistical evaluation methods. 1968, 1st edition, p. 436.
14. ^ Otfried Beyer, Horst Hackel: Probability calculation and mathematical statistics. 1976, p. 58.
15. ^ Otfried Beyer, Horst Hackel: Probability calculation and mathematical statistics. 1976, p. 101.
16. ↑ George G. Judge, R. Carter Hill, W. Griffiths, Helmut Lütkepohl , TC Lee. Introduction to the Theory and Practice of Econometrics. John Wiley & Sons, New York, Chichester, Brisbane, Toronto, Singapore, ISBN 978-0-471-62414-1 , second edition 1988, p. 40.
17. ↑ Hans-Otto Georgii: Introduction to Probability Theory and Statistics , ISBN 978-3-11-035970-1 , p. 102 (accessed via De Gruyter Online).
18. ↑ Hans-Heinz Wolpers: Mathematics lessons in the secondary level II. Volume 3: Didactics of stochastics. Year ?, p. 20.
19. ↑ George G. Judge, R. Carter Hill, W. Griffiths, Helmut Lütkepohl , TC Lee. Introduction to the Theory and Practice of Econometrics. John Wiley & Sons, New York, Chichester, Brisbane, Toronto, Singapore, ISBN 978-0-471-62414-1 , second edition 1988, p. 40.
20. ^ W. Zucchini, A. Schlegel, O. Nenadíc, S. Sperlich: Statistics for Bachelor and Master students. Springer, 2009, ISBN 978-3-540-88986-1 , p. 121.
21. ^ W. Zucchini, A. Schlegel, O. Nenadíc, S. Sperlich: Statistics for Bachelor and Master students. Springer, 2009, ISBN 978-3-540-88986-1 , p. 123.
22. ^ Ludwig Fahrmeir , Rita artist , Iris Pigeot , and Gerhard Tutz : Statistics. The way to data analysis. 8., revised. and additional edition. Springer Spectrum, Berlin / Heidelberg 2016, ISBN 978-3-662-50371-3 , p. 232.
23. ^ Ludwig Fahrmeir , Rita artist , Iris Pigeot , and Gerhard Tutz : Statistics. The way to data analysis. 8., revised. and additional edition. Springer Spectrum, Berlin / Heidelberg 2016, ISBN 978-3-662-50371-3 , p. 254.
24. ↑ Wolfgang Viertl, Reinhard Karl: Introduction to Stochastics: With elements of Bayesian statistics and the analysis of fuzzy information. Year ?, p. 49.
25. ↑ Ansgar Steland: Basic knowledge statistics. Springer, 2016, ISBN 978-3-662-49948-1 , p. 116, limited preview in the Google book search.
26. ^ ^{A b} Ludwig Fahrmeir , Rita artist , Iris Pigeot , and Gerhard Tutz : Statistics. The way to data analysis. 8., revised. and additional edition. Springer Spectrum, Berlin / Heidelberg 2016, ISBN 978-3-662-50371-3 , p. 233.
27. ↑ Gerhard Hübner: Stochastics: An application-oriented introduction for computer scientists, engineers and mathematicians. 3rd edition, 2002, p. 103.
28. ^ Lothar Papula: Mathematics for engineers and scientists. Volume 3: Vector analysis, probability calculation, mathematical statistics, error and compensation calculation. 1994, p. 338.
29. ^ Hans-Otto Georgii: Stochastics . Introduction to probability theory and statistics. 4th edition. Walter de Gruyter, Berlin 2009, ISBN 978-3-11-021526-7 , p. 108 , doi : 10.1515 / 9783110215274 .
30. ↑ Source: SOEP 2006 Height of the German Statistics of the Socio-Economic Panel (SOEP) , prepared by statista.org
31. ↑ Klenke: Probability Theory. 2013, p. 106.
32. ^ Ludwig Fahrmeir , Rita artist , Iris Pigeot , and Gerhard Tutz : Statistics. The way to data analysis. 8., revised. and additional edition. Springer Spectrum, Berlin / Heidelberg 2016, ISBN 978-3-662-50371-3 , p. 329.
33. ↑ L. Kruschwitz, S. Husmann: Financing and investment. Year ?, p. 471.
34. ^ Otfried Beyer, Horst Hackel: Probability calculation and mathematical statistics. 1976, p. 86.
35. ↑ Irénée-Jules Bienaymé: "Considérations à l'appui de la découverte de Laplace sur la loi de probabilité dans la méthode des moindres carrés", Comptes rendus de l'Académie des sciences Paris. 37, 1853, pp. 309-317.
36. ↑ Michel Loeve: Probability Theory. (= Graduate Texts in Mathematics. Volume 45). 4th edition, Springer-Verlag, 1977, ISBN 3-540-90210-4 , p. 12.
37. ^ Leo A. Goodman : On the exact variance of products. In: Journal of the American Statistical Association . December 1960, pp. 708-713. doi: 10.2307 / 2281592
38. ↑ Wolfgang Kohn: Statistics: data analysis and probability calculation. Year ?, p. 250.
39. ^ Otfried Beyer, Horst Hackel: Probability calculation and mathematical statistics. 1976, p. 97.
40. ^ Georg Neuhaus: Basic course in stochastics. Year ?, p. 290.
41. ↑ Jeffrey M. Wooldrige: Introductory Econometrics: A Modern Approach. 5th edition, 2012, p. 736.
42. ^ Toni C. Stocker, Ingo Steinke: Statistics: Basics and methodology. de Gruyter Oldenbourg, Berlin 2017, ISBN 978-3-11-035388-4 , p. 319.
43. ^ Ludwig Fahrmeir , Thomas Kneib , Stefan Lang, Brian Marx: Regression: models, methods and applications. Springer Science & Business Media, 2013, ISBN 978-3-642-34332-2 , p. 646.
44. ↑ George G. Judge, R. Carter Hill, W. Griffiths, Helmut Lütkepohl , TC Lee. Introduction to the Theory and Practice of Econometrics. John Wiley & Sons, New York, Chichester, Brisbane, Toronto, Singapore, ISBN 978-0-471-62414-1 , second edition 1988, p. 43.
45. ↑ George G. Judge, R. Carter Hill, W. Griffiths, Helmut Lütkepohl , TC Lee. Introduction to the Theory and Practice of Econometrics. John Wiley & Sons, New York, Chichester, Brisbane, Toronto, Singapore, ISBN 978-0-471-62414-1 , second edition 1988, p. 43.
46. ↑ Wilfried Hausmann, Kathrin Diener, Joachim Käsler: Derivatives, Arbitrage and Portfolio Selection: Stochastic Financial Market Models and Their Applications. 2002, p. 15.
47. ^ Ludwig Fahrmeir, Thomas Kneib, Stefan Lang, Brian Marx: Regression: models, methods and applications. Springer Science & Business Media, 2013, ISBN 978-3-642-34332-2 , p. 647.

This version was added to the list of articles worth reading on November 20, 2017 .