Disturbance and residual
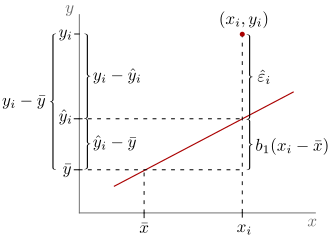
In statistics , disturbance and residual are two closely related concepts. The disturbance variables (not to be confused with disturbance parameters or disturbance factors ), also called disturbance variables , disturbance terms , error terms or errors for short , are unobservable random variables in a simple or multiple regression equation that measure the vertical distance between the observation point and the true straight line ( regression function of the population ). They are usually assumed to be uncorrelated , to have an expectation of zero and a homogeneous variance ( Gauss-Markov assumptions ). They include unobserved factors that affect the dependent variable. The disturbance can also contain measurement errors in the observed dependent or independent variables.
In contrast to the disturbance variables, residuals ( Latin residuum = “that which remained”) are calculated variables and measure the vertical distance between the observation point and the estimated regression line . Sometimes the residual is also referred to as the “estimated residual”. This naming is problematic because the disturbance variable is a random variable and not a parameter. There can therefore be no question of estimating the disturbance variable.
The problem with so-called regression diagnostics is that the Gauss-Markow assumptions only relate to the disturbance variables, but not to the residuals. Although the residuals also have an expected value of zero, they are not uncorrelated and do not show any homogeneous variance. In order to take this into account, the residuals are usually modified in order to meet the required assumptions, e.g. B. Studentized residuals. The sum of squares of the residuals plays an important role in statistics in many applications, e.g. B. the least squares method . The notation of the disturbance variables as or is based on the Latin word erratum (error). The residuals can be generated using the residual matrix.
Disturbance and residual
Disturbances are not to be confused with the residuals. A distinction is made between the two concepts as follows:
- Unobservable random disturbances : measure the vertical distance between the observation point and the theoretical ( true straight line )
- Residual : Measure the vertical distance between empirical observation and the estimated regression line
Simple linear regression
In simple linear regression with the single linear regression model , the ordinary residuals are given by
- .
These are residuals because an estimated value is subtracted from the true value . Specifically be said of the observation values of the adjusted values ( English fitted values ) subtracted. In simple linear regression, numerous assumptions are usually made about the disturbance variables (see Assumptions about the disturbance variables ).
Residual variance
The residual variance (also called residual variance) is an estimate of the variance of the regression function in the population . In simple linear regression, an estimate found by the maximum likelihood estimate is given by
- .
However, the estimator does not meet common quality criteria for point estimators and is therefore not used often. For example, the estimator is not unbiased for . In simple linear regression it can be shown under the assumptions of the classical model of linear single regression that an unbiased estimate of the variance of the disturbance variables , i.e. .h an estimate that is fulfilled is given by the variant adjusted for the number of degrees of freedom :
- .
The positive square root of this unbiased estimator is also known as the standard error of regression .
Residuals as a function of the disturbance variables
In simple linear regression, the residuals can be written as a function of the disturbance variables for each individual observation as
- .
Sum of the residuals
The KQ regression equation is determined so that the residual sum of squares becomes a minimum. Equivalently, this means that positive and negative deviations from the regression line cancel each other out. If the model of linear single regression contains an axis intercept that differs from zero, then it must be true that the sum of the residuals is zero
Multiple linear regression
Since the residuals, in contrast to the disturbance variables, are observable and calculated variables, they can be displayed graphically or examined in other ways. In contrast to simple linear regression, in which a straight line is determined, in multiple linear regression (extension of simple linear regression to regressors) a hyperplane is determined that runs through the point cloud. If there are two regressors, the observations are figuratively speaking above or below the regression level. The differences between the observed and the predicted values lying on the hyperplane represent the residuals.
- .
The residuals obtained by least squares estimation are called ordinary residuals . If there are additional observations, then the common SQ residuals in multiple linear regression are given by
- ,
where a projection matrix , or more precisely the idempotent and symmetrical residual matrix, represents and represents the KQ estimator in the multiple case.
properties
The ordinary residuals are in the mean , i. H.
The covariance matrix of the ordinary residuals is given by
- .
The ordinary residuals are thus heteroscedastic, there
- .
This means that the Gauss-Markov assumptions are not fulfilled for the ordinary residuals , since the homoscedasticity assumption does not apply.
With the help of the prediction and residual matrices, it can be shown that the residuals are uncorrelated with the predicted values
- .
Partial residuals
Partial residuals scatterplots are built using partial residuals that are defined by
- .
Studentized residuals
For this simple model, let the design matrix be
given. The prediction matrix is the matrix of the orthogonal projection onto the column space of the design matrix . is given by
- .
The statistical leverage values are the -th diagonal elements of the prediction matrix. The variance of the -th residual is given by
- .
In this case the design matrix has only two columns, which leads to the following variance
- .
The corresponding studentized residuals are
- .
The Studentized residuals are distributed identically (but not independently) and are therefore particularly homoscedastic. They could thus represent a solution to the violation of the homoscedasticity assumption.
Building dimensions
Residual Sum of Squares
If one forms the sum of the squared residuals for all observations, one obtains the residual squared sum :
- .
This particular square sums of deviation appears in many statistical measures, such as B. the coefficient of determination , the F statistic and various standard errors , such as the standard error of regression . The minimization of the sum of squares leads to the least squares estimator.
See also
- Middle absolute error
- Special residuals in survival time analysis :
Individual evidence
- ↑ Ulrich Kockelkorn: Linear statistical methods. De Gruyter 2018, 978-3-486-78782-5, p. 281 (accessed via De Gruyter Online).
- ^ Ludwig Fahrmeir , Thomas Kneib , Stefan Lang, Brian Marx: Regression: models, methods and applications. Springer Science & Business Media, 2013, ISBN 978-3-642-34332-2 , p. 109.
- ↑ Jeffrey Marc Wooldridge : Introductory econometrics: A modern approach. 4th edition. Nelson Education, 2015, p. 55.
- ↑ Manfred Precht and Roland Kraft: Bio-Statistics 2: Hypothesis tests – analysis of variance – non-parametric statistics – analysis of contingency tables – correlation analysis – regression analysis – time series analysis – program examples in MINITAB, STATA, N, StatXact and TESTIMATE : 5., completely revised. Edition Reprint 2015, De Gruyter, Berlin June 2015, ISBN 978-3-486-78352-0 (accessed from De Gruyter Online), p. 299.
- ^ Rainer Schlittgen: Regression analyzes with R. , ISBN 978-3-486-73967-1 , p. 25 (accessed via De Gruyter Online).
- ^ Ludwig Fahrmeir , Thomas Kneib , Stefan Lang, Brian Marx: Regression: models, methods and applications. Springer Science & Business Media, 2013, ISBN 978-3-642-34332-2 , p. 77.
- ^ Rainer Schlittgen : Regression analyzes with R. , ISBN 978-3-486-73967-1 , p. 27 (accessed via De Gruyter Online).
- ^ Rainer Schlittgen: Regression analyzes with R. , ISBN 978-3-486-73967-1 , p. 27 (accessed via De Gruyter Online).