Hyperplane

A hyperplane (blue) in the viewing area is produced by shifting an original plane by a vector (red).

In mathematics, a hyperplane is a generalization of the concept of the plane from visual space to spaces of any dimension . Similar to how a plane in three-dimensional space can be described by a support vector and two direction vectors , a hyperplane in -dimensional space is represented by a support vector and direction vectors. In the -dimensional coordinate space , a hyperplane is the set of solutions to a linear equation with unknowns. Hyperplanes therefore play an important role in the solution structure of linear systems of equations and inequalities . ${\displaystyle n}$ ${\displaystyle n-1}$ ${\displaystyle n}$ ${\displaystyle n}$

In linear algebra , hyperplanes are also considered in infinite-dimensional vector spaces and there are precisely the affine subspaces with codimension one. Each hyperplane is created by shifting a subspace by a fixed vector . If the zero vector can be selected, one also speaks of a linear hyperplane , since the hyperplane itself then represents a vector space. For a better differentiation, one speaks of an affine hyperplane in the case of any displacement vector .

Every subspace with codimension one can also be characterized as the core of a linear functional . In functional analysis , closed hyperplanes are particularly considered, which are described by continuous linear functionals. In projective geometry , projective hyperplanes are also examined as projective subspaces with codimension one. An even more generalized hyperplane concept can be found in matroid theory .

Euclidean geometry

definition

Parametric representation of a hyperplane in three-dimensional space

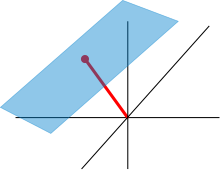
A hyperplane in -dimensional Euclidean space is a subset of the form ${\displaystyle n}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle H\subset \mathbb {R} ^{n}}$

${\displaystyle H=\{x\in \mathbb {R} ^{n}\mid x=p+s_{1}u_{1}+\dotsb +s_{n-1}u_{n-1}~{\text{mit}}~s_{1},\dotsc ,s_{n-1}\in \mathbb {R} \}}$,

where is a support vector of the hyperplane and are linearly independent direction vectors of the hyperplane. The direction vectors spanning an affine coordinate system , the affine coordinates of a point on the hyperplane. ${\displaystyle p\in \mathbb {R} ^{n}}$ ${\displaystyle u_{1},\dotsc ,u_{n-1}\in \mathbb {R} ^{n}}$ ${\displaystyle (s_{1},\dotsc ,s_{n-1})}$

Examples

• In one-dimensional Euclidean space, each point represents a hyperplane.
• In two-dimensional Euclidean space, every straight line represents a hyperplane.
• In three-dimensional Euclidean space, each plane represents a hyperplane.

Further representations

In addition to the above parameter form , there are other forms of representation for hyperplanes. In normal form , the representation is a hyperplane

${\displaystyle H=\{x\in \mathbb {R} ^{n}\mid \langle v,x-p\rangle =0\}}$,

where is a normal vector of the hyperplane, is again a support vector of the hyperplane and denotes the standard scalar product of two vectors. In Hessian normal form , a hyperplane has the corresponding representation ${\displaystyle v\in \mathbb {R} ^{n}\setminus \{0\}}$ ${\displaystyle p\in \mathbb {R} ^{n}}$ ${\displaystyle \langle \cdot ,\cdot \rangle }$

${\displaystyle H=\{x\in \mathbb {R} ^{n}\mid \langle v_{0},x\rangle =d\}}$,

where is a normalized and oriented normal vector of the hyperplane and describes the distance of the hyperplane from the coordinate origin . The Hessian normal form allows an efficient calculation of the distance of any point in space from the hyperplane. ${\displaystyle v_{0}\in \mathbb {R} ^{n}\setminus \{0\}}$ ${\displaystyle d\in \mathbb {R} _{0}^{+}}$

The representation of a hyperplane is in coordinate form

${\displaystyle H=\{(x_{1},\dotsc ,x_{n})\in \mathbb {R} ^{n}\mid a_{1}x_{1}+\dotsb +a_{n}x_{n}=b\}}$,

where are and at least one of the coefficients is non-zero. The coordinate form results from the normal form by multiplying it out, with and being set. ${\displaystyle a_{1},\dotsc ,a_{n},b\in \mathbb {R} }$ ${\displaystyle a_{1},\dotsc ,a_{n}}$ ${\displaystyle a_{1}=v_{1},\dotsc ,a_{n}=v_{n}}$ ${\displaystyle b=\langle v,p\rangle }$

use

The set of solutions of a linear system of equations with equations and unknowns is the intersection of hyperplanes in -dimensional space (in the picture is ) ${\displaystyle m}$ ${\displaystyle n}$ ${\displaystyle m}$ ${\displaystyle n}$ ${\displaystyle m=n=3}$

As can be seen from the coordinate form, the solution set represents a linear equation with unknowns of the form ${\displaystyle n}$

${\displaystyle a_{1}x_{1}+\dotsb +a_{n}x_{n}=b}$

represents a hyperplane in -dimensional Euclidean space. Each line of a linear system of equations therefore describes such a hyperplane. The solution set of the linear system of equations is then the intersection of all these hyperplanes. Correspondingly, the solution set describes a linear inequality of the form ${\displaystyle n}$

${\displaystyle a_{1}x_{1}+\dotsb +a_{n}x_{n}\leq b}$

a half-space in -dimensional Euclidean space, which is bounded by a hyperplane. The solution set of a linear system of inequalities is then the intersection of such half spaces and thus represents a convex polytope , for example a hypercube , a hyper rectangle or a simplex (hypertenrahedron). The linear optimization deals with methods for maximizing a given linear objective function as in a convex polytope. ${\displaystyle n}$

A hyperplane is called a supporting hyperplane of a given set in Euclidean space if it intersects the boundary of the set and the set lies completely in one of the two closed half-spaces defined by the hyperplane. If the set is convex, then there is such a supporting hyperplane for each boundary point of the set.

After the set of Stone-Tukey ( English Ham sandwich theorem ) can be limited measurable amounts in are bisected by a hyperplane at the same time each -dimensional Euclidean space. ${\displaystyle n}$ ${\displaystyle n}$

Linear Algebra

In linear algebra , the concept of the hyperplane is generalized to vector spaces over arbitrary bodies and arbitrary dimensions .

definition

If a vector space is above the body , then a hyperplane is a subset of the shape ${\displaystyle V}$ ${\displaystyle K}$ ${\displaystyle H\subset V}$

${\displaystyle H=p+U=\{p+u\mid u\in U\}}$,

where is an arbitrary vector and a subspace of with codimension . Hyperplanes are accordingly maximal true affine subspaces , that is, every true affine subspace is contained in a hyperplane. A hyperplane is called a linear hyperplane if it contains the zero vector , that is, if it can be chosen in the definition . ${\displaystyle p\in V}$ ${\displaystyle U}$ ${\displaystyle V}$ ${\displaystyle 1}$ ${\displaystyle p=0}$

Examples

In the following examples, let a field of the characteristic , for example the real or complex numbers . ${\displaystyle K}$ ${\displaystyle 0}$

• In coordinate space , the coordinate vectors that satisfy a linear equation of the form represent a hyperplane. If , it is a linear hyperplane. ${\displaystyle K^{n}}$ ${\displaystyle a_{1}x_{1}+\dotsb +a_{n}x_{n}=b}$ ${\displaystyle b=0}$
• In the matrix space , the matrices for which the sum of all entries is constant represent a hyperplane. If this is constant , it is a linear hyperplane. ${\displaystyle K^{m\times n}}$ ${\displaystyle 0}$
• In the polynomial space , the polynomials of the form , which is fixed, represent a hyperplane. In this case , it is a linear hyperplane. ${\displaystyle K[X]}$ ${\displaystyle c+a_{1}X+\dotsb +a_{n}X^{n}}$ ${\displaystyle c\in K}$ ${\displaystyle c=0}$
• In the function room which provide functions with a firm and is a hyperplane. In the case , these are a linear hyperplane. ${\displaystyle V^{D}}$ ${\displaystyle f\colon D\to V}$ ${\displaystyle f(x_{0})=f_{0}}$ ${\displaystyle x_{0}\in D}$ ${\displaystyle f_{0}\in V}$ ${\displaystyle f_{0}=0}$

Further representations

Since every subspace of the codimension can also be characterized as the core of a linear functional that is not the zero functional , a hyperplane has the representation ${\displaystyle 1}$ ${\displaystyle f\colon V\to K}$

${\displaystyle H=p+\operatorname {ker} f}$.

By setting , the equivalent representation results ${\displaystyle d=f(p)}$

${\displaystyle H=\{v\in V\mid f(v)=d\}}$.

Here, and for a given hyperplane are only clearly determined up to a common factor. Conversely, the archetype represents a hyperplane for every linear functional that is not equal to the zero functional and for every scalar . ${\displaystyle f}$ ${\displaystyle d}$ ${\displaystyle f^{-1}(d)}$ ${\displaystyle f}$ ${\displaystyle d}$

These statements remain valid even if an inclined body and a left vector space is over . ${\displaystyle K}$ ${\displaystyle V}$ ${\displaystyle K}$

use

In functional analysis , one considers infinite-dimensional vector spaces above or , on which a topology is explained that makes them topological vector spaces . Here one is particularly interested in hyperplanes which are defined by continuous linear functionals . Since a linear functional is continuous exactly when its core is closed, the continuous linear functionals unequal to the zero functional precisely define the closed hyperplanes. For normalized spaces , more generally locally convex spaces , there are, according to Hahn-Banach's theorem, a great number of such continuous linear functionals and thus also closed hyperplanes of form ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {C} }$

${\displaystyle H=\{v\in V\mid \operatorname {Re} (f(v))=d\}}$

with . This richness is reflected in the separation theorem , according to which two disjoint convex, compact sets can be separated by such a closed hyperplane . ${\displaystyle d\in \mathbb {R} }$

The separation property can also be generalized for affine spaces over arranged bodies with the concept of (strong) side division . Even for non-Desargue affine planes there is in certain cases a (weak) division of the sides by straight lines.

Projective geometry

definition

If the projective space is the vector space , then a (projective) hyperplane is a subset of the form ${\displaystyle P(V)}$ ${\displaystyle V}$ ${\displaystyle H\subset P(V)}$

${\displaystyle H=(U\setminus \{0\})/\sim }$,

where a sub-vector space of codimension is one and the equivalence relation identifies scalar multiples of vectors not equal to the zero vector with one another. The hyperplanes in are therefore precisely the projective subspaces of codimension one. A projective hyperplane itself represents a projective space, specifically space . If -dimensional, then -dimensional and -dimensional. ${\displaystyle U}$ ${\displaystyle V}$ ${\displaystyle \sim }$ ${\displaystyle P(V)}$ ${\displaystyle P(U)}$ ${\displaystyle V}$ ${\displaystyle (n+1)}$ ${\displaystyle P(V)}$ ${\displaystyle n}$ ${\displaystyle P(U)}$ ${\displaystyle (n-1)}$

Examples

If the underlying vector space is Euclidean space , then there are the following equivalents: ${\displaystyle V}$ ${\displaystyle \mathbb {R} ^{n}}$

• A hyperplane (a point) on the projective straight line corresponds to a straight line through the origin in the Euclidean plane . ${\displaystyle P(\mathbb {R} ^{2})}$ ${\displaystyle \mathbb {R} ^{2}}$
• A hyperplane (a straight line) in the projective plane corresponds to an original plane in Euclidean space . ${\displaystyle P(\mathbb {R} ^{3})}$ ${\displaystyle \mathbb {R} ^{3}}$
• A hyperplane (a plane) in projective space corresponds to an original hyperplane in Euclidean space . ${\displaystyle P(\mathbb {R} ^{4})}$ ${\displaystyle \mathbb {R} ^{4}}$

Coordinate representation

Homogeneous coordinates of two projective hyperplanes and in the projective plane ${\displaystyle g}$ ${\displaystyle h}$ ${\displaystyle P(\mathbb {R} ^{3})}$

If the homogeneous coordinates of a point are in the -dimensional projective standard space , then a projective hyperplane has the coordinate representation ${\displaystyle (x_{0}\colon x_{1}\colon \ldots \colon x_{n})}$ ${\displaystyle n}$ ${\displaystyle P(K^{n+1})}$ ${\displaystyle H\subset P(K^{n+1})}$

${\displaystyle H=\{(x_{0}\colon x_{1}\colon \ldots \colon x_{n})\in P(K^{n+1})\mid a_{0}x_{0}+a_{1}x_{1}+\dotsb +a_{n}x_{n}=0\}}$,

where are and at least one of the coefficients is non-zero. ${\displaystyle a_{0},\dotsc ,a_{n}\in K}$ ${\displaystyle a_{0},\dotsc ,a_{n}}$

However, a non-Desargue projective plane cannot be coordinated in this way. There the hyperplanes are by definition the straight lines.

Relation to affine spaces

If a hyperplane is in a projective space , then the set represents ${\displaystyle H}$ ${\displaystyle P}$

${\displaystyle A=\varphi (P\setminus H)}$

an affine space represents, wherein a corresponding embedding of in is. The translation space of is precisely the associated sub-vector space . The points from are then actually called, the points from improper or distant points . Conversely, every affine space can be transformed into a projective space by disjoint union with a remote hyperplane of the same dimension ${\displaystyle \varphi \colon P\to A}$ ${\displaystyle P}$ ${\displaystyle A}$ ${\displaystyle A}$ ${\displaystyle H}$ ${\displaystyle U}$ ${\displaystyle A}$ ${\displaystyle H}$

${\displaystyle P=\varphi ^{-1}(A)\;\;\!\!{\dot {\cup }}\;\;\!\!H}$

expand. For example, if and , then the associated embedding is with the inverse . ${\displaystyle P=P(K^{n+1})}$ ${\displaystyle H=\{(0\colon x_{1}\colon \ldots \colon x_{n})\mid x_{1},\dotsc ,x_{n}\in K\}}$ ${\displaystyle \varphi \colon (x_{0}\colon \ldots \colon x_{n})\mapsto (x_{1}/x_{0},\dotsc ,x_{n}/x_{0})}$ ${\displaystyle \varphi ^{-1}\colon (x_{1},\dotsc ,x_{n})\mapsto (1\colon x_{1}\colon \ldots \colon x_{n})}$

use

An application of projective hyperplanes in algebraic geometry and algebraic topology is offered by Lefschetz's theorem on hyperplane cuts , which establishes a connection between the shape of a complex projective variety and the shape of its sub- varieties .

In finite geometry , among the finite affine or projective geometries, those special properties have, in which - besides the ordinary points as a point set - especially the hyperplanes of space are chosen as a block set .

See also

• Hypersurface , a generalization of hyperplanes to curved manifolds
• Household transformation , the reflection of a vector on a hyperplane

literature

Real geometry and functional analysis

• Hans Wilhelm Alt : Linear Functional Analysis . An application-oriented introduction. 5th edition. Springer, Berlin 2006, ISBN 3-540-34186-2 .
• Harro Heuser : Textbook of Analysis . Volumes I and II. Teubner, Wiesbaden 2003, ISBN 3-519-62233-5 .
• Harro Heuser: Functional Analysis. Theory and application . 3. Edition. Teubner, Wiesbaden 1992, ISBN 3-519-22206-X .

Linear algebra and analytic geometry

• Hermann Schaal: Linear Algebra and Analytical Geometry, Volumes I and II . 2nd revised edition. Vieweg, Braunschweig 1980, ISBN 3-528-13057-1 .
• Günter Scheja, Uwe Storch: Textbook of Algebra: including linear algebra . 2., revised. and exp. Edition. Teubner, Stuttgart 1994, ISBN 3-519-12203-0 .
• Uwe Storch, Hartmut Wiebe: Textbook of mathematics for mathematicians, computer scientists and physicists . Volume II: Linear Algebra . BI-Wissenschafts-Verlag, 1990, ISBN 3-411-14101-8 .

Applications in geometry (page division)

• Wendelin Degen and Lothar Profke: Fundamentals of affine and Euclidean geometry . Teubner, Stuttgart 1976, ISBN 3-519-02751-8 .
• Emanuel Sperner : The ordering functions of a geometry . In: Math. Ann. tape 121 . Teubner, 1949, p. 107-130 .

Web links

Wiktionary: Hyperplane  - explanations of meanings, word origins, synonyms, translations

• MI Voitsekhovskii: Hyperplane . In: Michiel Hazewinkel (Ed.): Encyclopaedia of Mathematics . Springer-Verlag , Berlin 2002, ISBN 978-1-55608-010-4 (English, online ).
• Eric W. Weisstein : Hyperplane . In: MathWorld (English).
• georgiosl: hyperplane . In: PlanetMath . (English)

Individual evidence

1. ↑ Klemens Burg, Herbert Haf, Friedrich Wille, Andreas Meister: Higher Mathematics for Engineers Volume II: Linear Algebra . Springer, 2012, ISBN 978-3-8348-2267-3 , pp. 81 .
2. ↑ ^{a b} Hermann Schichl , Roland Steinbauer: Introduction to the mathematical work . Springer, 2012, ISBN 978-3-642-28646-9 , pp. 462 .
3. ↑ ^{a b} Peter Knabner, Wolf Barth: Lineare Algebra: Fundamentals and Applications . Springer, 2012, ISBN 978-3-642-32186-3 , pp. 41-42 .
4. ^ Rainer E. Burkard, Uwe T. Zimmermann: Introduction to Mathematical Optimization . Springer, 2012, ISBN 978-3-642-28673-5 , pp. 24 .
5. ^ Rainer E. Burkard, Uwe T. Zimmermann: Introduction to Mathematical Optimization . Springer, 2012, ISBN 978-3-642-28673-5 , pp. 247 .
6. ↑ ^{a b c} Max Koecher: Linear Algebra and Analytical Geometry . Springer, 2012, ISBN 978-3-642-96772-6 , pp. 167 .
7. ^ RV Kadison , JR Ringrose : Fundamentals of the Theory of Operator Algebras, Volume I , Academic Press (1983), ISBN 0-12-393301-3 , Corollary 1.2.5