Support hyperplane

Support hyperplane (dashed line) and the corresponding support half-space (light blue) of a set S (purple)

A supporting hyperplane or supporting hyperplane is in the mathematics a hyperplane that the edge of a given subset of Euclidean space so cut that the amount entirely in one of the two defined by the hyperplane completed half spaces located. In two- and three-dimensional space, one speaks accordingly of a supporting line or a supporting plane . For a convex set there is a supporting hyperplane at every boundary point, which is even unique in the case of smooth convex sets .

definition

Is a lot of in -dimensional Euclidean space with edge , it means a hyperplane supporting hyperplane of when ${\displaystyle S\subseteq \mathbb {R} ^{n}}$ ${\displaystyle n}$ ${\displaystyle \partial S}$ ${\displaystyle H\subset \mathbb {R} ^{n}}$ ${\displaystyle S}$

${\displaystyle H\cap \partial S\neq \emptyset }$

and

${\displaystyle S\subseteq H^{+}}$   or   ${\displaystyle S\subseteq H^{-}}$

apply where and the two closed half-spaces to be. The half-space that fulfills the second condition is then called the supporting half-space of . An edge point of which lies on a support hyperplane is also called a support point of . A supporting hyperplane actually means if is, otherwise improper . ${\displaystyle H^{+}}$ ${\displaystyle H^{-}}$ ${\displaystyle H}$ ${\displaystyle S}$ ${\displaystyle S}$ ${\displaystyle S}$ ${\displaystyle S\not \subset H}$

presentation

If an edge point of and denotes the standard scalar product im , then is the hyperplane ${\displaystyle r\in \partial S}$ ${\displaystyle S}$ ${\displaystyle \langle \cdot ,\cdot \rangle }$ ${\displaystyle \mathbb {R} ^{n}}$

${\displaystyle H=\{x\in \mathbb {R} ^{n}\mid \langle v,x\rangle =\langle v,r\rangle \}}$

with normal vector a support hyperplane of through the support point if and only if ${\displaystyle v\in \mathbb {R} ^{n}\setminus \{0\}}$ ${\displaystyle S}$ ${\displaystyle r}$

${\displaystyle \langle v,s\rangle \geq \langle v,r\rangle }$

for all points or ${\displaystyle s\in S}$

${\displaystyle \langle v,s\rangle \leq \langle v,r\rangle }$

applies to all . By orienting the normal vector, for example in the direction of the set , one can restrict oneself to one of the two cases. ${\displaystyle s\in S}$ ${\displaystyle S}$

Support hyperplanes for convex sets

In the case of a non-convex set there are edge points at which no supporting hyperplane exists

Existence proposition

The following existence theorem for convex sets goes back to Hermann Minkowski (1896):

In the case of a convex subset of Euclidean space, each boundary point has at least one supporting hyperplane.

This means that for a convex set there is a vector for every edge point , so that ${\displaystyle S\subseteq \mathbb {R} ^{n}}$ ${\displaystyle r\in \partial S}$ ${\displaystyle v\in \mathbb {R} ^{n}\setminus \{0\}}$

${\displaystyle \langle v,s\rangle \geq \langle v,r\rangle }$

applies to all . In the case of a convex set, all edge points are support points. ${\displaystyle s\in S}$

proof

Let with be a sequence of points outside the closure of that converges to the boundary point ( ). According to the separation theorem, there is now a hyperplane through every point ${\displaystyle (r_{k})_{k\in \mathbb {N} }}$ ${\displaystyle r_{k}\in \mathbb {R} ^{n}\setminus {\bar {S}}}$ ${\displaystyle S}$ ${\displaystyle r}$ ${\displaystyle r_{k}\to r}$ ${\displaystyle r_{k}}$

${\displaystyle H_{k}=\{x\in \mathbb {R} ^{n}\mid \langle v_{k},x\rangle =\langle v_{k},r_{k}\rangle \}}$,

so that applies. If the vectors are now normalized to length one , then the sequence is restricted and thus contains a convergent subsequence according to Bolzano-Weierstrass's theorem . If the limit of such a partial sequence is ( ), then results ${\displaystyle S\subset H_{k}^{+}}$ ${\displaystyle v_{k}}$ ${\displaystyle (v_{k})_{k\in \mathbb {N} }}$ ${\displaystyle ({\tilde {v}}_{k})_{k\in \mathbb {N} }}$ ${\displaystyle v}$ ${\displaystyle {\tilde {v}}_{k}\to v}$

${\displaystyle \langle v,r\rangle =\lim _{k\to \infty }\langle {\tilde {v}}_{k},r_{k}\rangle \leq \lim _{k\to \infty }\langle {\tilde {v}}_{k},s\rangle =\langle v,s\rangle }$

for everyone . That’s the hyperplane ${\displaystyle s\in S}$

${\displaystyle H=\{x\in \mathbb {R} ^{n}\mid \langle v,x\rangle =\langle v,r\rangle \}}$

a support hyperplane in the support point with the associated support half-space . ${\displaystyle r}$ ${\displaystyle H^{+}}$

Remarks

The support hyperplane through a given support point need not be unique

If the set has a non-empty interior , so is , then the converse also holds and is convex if all edge points are support points. This results in the following characterization of convex sets: ${\displaystyle S}$ ${\displaystyle S^{\circ }\neq \emptyset }$ ${\displaystyle S}$ ${\displaystyle S}$

A subset of Euclidean space with a non-empty interior is convex if and only if all of its boundary points are support points.

The set is strictly convex if each supporting hyperplane contains exactly one support point. In the case of a strictly convex set, the supporting hyperplanes for different support points are also different and each edge point of the set is an extreme point . A related result is Minkowski's theorem . ${\displaystyle S}$ ${\displaystyle S}$

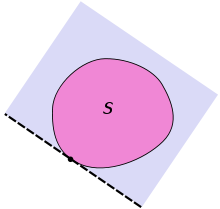
However, a support hyperplane through a given support point does not necessarily have to be clearly defined, as the example in the adjacent figure shows. Convex sets, for which the supporting hyperplane is unique through a given boundary point, are called smooth convex . They play an important role in the theory of smooth spaces .

generalization

Support hyperplanes are also considered more generally in any topological vector spaces . A support hyperplane on a subset of a topological vector space at the edge point is then a real hyperplane ${\displaystyle S\subseteq V}$ ${\displaystyle V}$ ${\displaystyle r\in \partial S}$

${\displaystyle H=\{v\in V\mid f(v)=f(r)\}}$,

where is a real linear functional which is not the zero functional and thereby the inequality ${\displaystyle f\colon V\rightarrow \mathbb {R} }$

${\displaystyle f(s)\geq f(r)}$

fulfilled for all . Such a functional is also referred to as a support functional on . If a given edge point has such a support hyperplane (and thus such a support functional), it is referred to as the support point of the subset . ${\displaystyle s\in S}$ ${\displaystyle S}$ ${\displaystyle r\in \partial S}$ ${\displaystyle S}$

See also

• Equal thickness , an area in which all parallel supporting lines have the same distance
• Support line
• Support point
• Support vector

literature

• Rainer E. Burkard, Uwe T. Zimmermann: Introduction to Mathematical Optimization . Springer, 2012, ISBN 978-3-642-28673-5 .
• Peter Gritzmann: Fundamentals of Mathematical Optimization . Springer, 2013, ISBN 978-3-8348-2011-2 .
• Dieter Jungnickel: Optimization Methods: An Introduction . Springer, 2014, ISBN 978-3-642-54821-5 .
• Gottfried Köthe: Topological linear spaces I . Springer, 2013, ISBN 978-3-662-24912-3 .
• Jürg T. Marti: Convex Analysis . Springer, 2013, ISBN 978-3-0348-5910-3 .

Individual evidence

1. ↑ ^{a b c} Rainer E. Burkard, Uwe T. Zimmermann: Introduction to Mathematical Optimization . Springer, 2012, p. 247 .
2. ↑ Peter Gritzmann: Fundamentals of mathematical optimization . Springer, 2013, p. 261 .
3. ↑ Dieter Jungnickel: Optimization Methods: An Introduction . Springer, 2014, p. 35 .
4. ^ Hermann Minkowski: Geometry of Numbers . Leipzig 1896.
5. ↑ Gottfried Köthe: Topological linear spaces I . Springer, 2013, p. 346 .
6. ↑ Jürg T. Marti: Convex Analysis . Springer, 2013, p. 108 .
7. ↑ Gottfried Köthe: Topological linear spaces I . Springer, 2013, p. 196 .
8. ↑ Jürg T. Marti: Convex Analysis . Springer, 2013, p. 66-67 .

Web links

• Supporting hyperplane . In: Michiel Hazewinkel (Ed.): Encyclopaedia of Mathematics . Springer-Verlag , Berlin 2002, ISBN 978-1-55608-010-4 (English, online ).