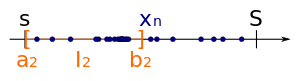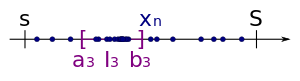Bolzano-Weierstrass theorem
The Bolzano-Weierstrass theorem (after Bernard Bolzano and Karl Weierstrass ) is an analysis theorem about the existence of convergent subsequences .
Formulations of the Bolzano-Weierstrass theorem
The Bolzano-Weierstrass theorem has the following formulations, all of which are equivalent to one another:
- Every bounded sequence of complex numbers (with infinitely many terms) contains (at least) one convergent subsequence .
- Every bounded sequence of complex numbers (with infinitely many terms) has (at least) one accumulation point .
- Every bounded sequence of real numbers has a largest and a smallest accumulation point.
Evidence sketch
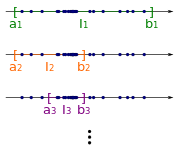
The proof of the general statements is reduced to the one-dimensional real statement. This can prove it by a same interval nesting and a subsequence designed so that each applies . These two sequences are constructed recursively.
- The starting point is the interval , where L is a bound of the sequence, i.e. H. all subsequent members are included in the interval. The first element of the partial sequence to be determined can also be set.
- In the step from k to k + 1 , the interval contains an infinite number of subsequent members.
- First the interval is halved in and with the center point .
- There cannot only be a finite number of subsequent members in both sub-intervals. A subinterval with an infinite number of sequence elements can always be selected; this half is denoted by.
- Finally, the next link is the sub-sequence as the first element determines the in and whose index than that of the previously selected element is greater, .
- The recursion step is performed for all . The observed interval becomes smaller and smaller, the length converges to zero, as is required from an interval nesting. According to the construction, the common point of all intervals is also the limit value of the partial sequence , and thus an accumulation point of the specified restricted sequence.
In order to determine the largest accumulation point, one must, whenever possible, select the upper sub-interval and the lower sub-interval for the smallest accumulation point.
The proof is based crucially on the interval nesting principle , which in turn is equivalent to the completeness of the real numbers.
Visualization of the evidence sketch
Generalizations
Finite-dimensional vector spaces
In the context of this theorem, the complex numbers are viewed as a two-dimensional real vector space. For a sequence of column vectors with n real components, one first selects a subsequence that converges in the first component. From this one again selects a partial sequence which also converges in the second component. The convergence in the first component is retained, since partial sequences of convergent sequences are again convergent with the same limit value. And so on, until the nth subsequence also converges in the last component.
Infinite-dimensional vector spaces
Bolzano-Weierstrass's theorem does not hold in infinite-dimensional normed vector spaces. So is z. B. limits the sequence of unit vectors (0,0, ..., 0,1,0, ..., 0, ...) in the sequence space , but has no accumulation point, since all sequence members have a distance of from each other. This counterexample can be generalized to any infinite-dimensional normalized spaces ; one can always construct an infinite sequence of vectors of length 1, which are paired with a distance of at least 1/2 .
As a substitute for Bolzano-Weierstrasse's theorem in infinite-dimensional vector spaces, the following statement exists in reflexive spaces : Every limited sequence of a reflexive space has a weakly convergent partial sequence. Together with Sobolev's embedding theorems , the existence of weakly convergent partial sequences of bounded sequences often provides solutions to variational problems and thus partial differential equations .
Conclusions and Generalizations
From Bolzano-Weierstrasse's theorem it follows that every monotonic and bounded sequence of real numbers converges ( monotonicity criterion ) and that a continuous function takes on a maximum or a minimum on a closed and bounded interval ( theorem of minimum and maximum ).
The Bolzano-Weierstrass theorem is closely related to the Heine-Borel theorem . A generalization of both theorems to topological spaces is as follows: A topological space is a compact space if and only if every network has a convergent subnet.
literature
- Konrad Königsberger : Analysis 1 . Springer, Berlin 2004, ISBN 3-540-41282-4
- Konrad Königsberger : Analysis 2. Springer-Verlag, Berlin / Heidelberg, 2000, ISBN 3-540-43580-8
![(I_ {k} = [u_ {k}, v_ {k}]) _ {{k \ in \ mathbb {N}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22d032974b6c2b5eeaa5bb6e04e40e8a3579bf91)



![I_ {1} = [u_ {1}, v_ {1}] = [- L, \, L]](https://wikimedia.org/api/rest_v1/media/math/render/svg/5eedc0bc205b4ab8ae350661a5e84bae73e54305)

![I_ {k} = [u_ {k}, v_ {k}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/e4b652920a1c6053563bd436b8fb45153dd682a4)
![[u_ {k}, t_ {k}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/61ff835c84d41e8560dd065cc07d126884c5bb75)
![[t_ {k}, v_ {k}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f7b84c9a615b409ae43f1813447d4947eb327c9)












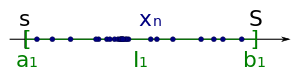
![{\ displaystyle I_ {1} = [s, S]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58be63fbf6d3dff28ca6747569a558d5af61740e)