Normal vector
In the geometry is a normal vector , and normal vector , a vector which is orthogonal (i. E. Perpendicular, vertical) on a straight line , curve , plane (curved) surface , or a higher-dimensional generalization is of such an object. A straight line with this vector as a directional vector is called a normal. A normal unit vector or a unit normal is a normal vector of length 1.
This article first deals with the case of straight lines in the plane and of planes in three-dimensional space ( linear algebra and analytic geometry ), then the case of curves in the plane and surfaces in space ( differential geometry ).
Linear algebra and analytic geometry
In this section, the variables for vectors are indicated by vector arrows, as is common in school mathematics.
Normal and normal vector of a straight line
A normal vector of a straight line in the plane is a vector different from the zero vector that is perpendicular to this straight line, i.e. the direction vector of a straight line that is perpendicular to , i.e. an orthogonal or normal to .
Has the direction vector , the two vectors and normal vectors. If one traverses the straight line in the direction of , then points to the left and to the right.
Is the straight line in the slope form by the equation
given, the vector is a direction vector of the straight lines and and are normal vectors. For so any normal has the slope . If , that is, horizontal, then every normal is vertical, so it has an equation of the form .
Is the straight line in general form
given, then is a normal vector.
A normal unit vector can be calculated from a normal vector by dividing by its length ( norm , amount). The vector is therefore normalized.
The second normal unit vector is obtained by multiplying the above normal unit vector by . Each normal vector can be formed by multiplying a normal unit vector by a real number not equal to zero.
Normal and normal vector of a plane
A normal vector of a plane in three-dimensional space is a vector different from the zero vector that is perpendicular to this plane, i.e. the directional vector of a straight line that is perpendicular to , i.e. an orthogonal or normal to .
Is the plane in the coordinate form by the equation
given, then is a normal vector.
If and is given by two spanning vectors (point-direction form or parametric form ), the condition that the normal vector is perpendicular to and leads to a linear system of equations for the components of :
Each of the different solutions provides a normal vector.
Another way to determine normal vectors is to use the cross product :
is a vector that is perpendicular to and , and in this order they form a legal system .
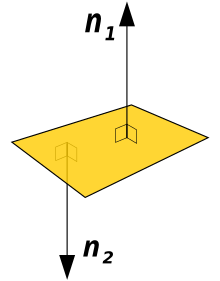
Has the equation
- ,
so is an upward and a downward normal vector.
As in the case of the straight line in the plane, a normal vector is obtained from a normal vector by dividing it by its length, a second by multiplying by and all other normal vectors by multiplying by real numbers.
A plane is clearly defined by a normal vector and a point lying on the plane, see normal form and Hessian normal form .
Normal vectors of curves and surfaces
Flat curves
In analysis and differential geometry , the normal vector to a plane curve (at a certain point) is a vector that is orthogonal (perpendicular) to the tangential vector at this point. The straight line in the direction of the normal vector through this point is called the normal , it is orthogonal to the tangent .
If the curve is given as a graph of a differentiable function , the tangent at the point has the slope , so the slope of the normal is
The normal in the point is then given by the equation
so through
given.
Is the plane curve in parameter form given , then a tangent vector at the point and a normal vector pointing to the right. As is customary in differential geometry, the point here denotes the derivative according to the curve parameter.
In the case of space curves , the normal vectors at a point (as in the case of straight lines in space) form a two-dimensional sub - vector space . In elementary differential geometry, one chooses a unit vector that points in the direction in which the curve is curved. This is called the principal normal (unit) vector , see Frenet's formulas .
Areas in three-dimensional space
Correspondingly, the normal vector of a curved surface at one point is the normal vector of the tangential plane at this point.
Is the area through the parametric representation
given, the two vectors are
- and
Clamping vectors of the tangential plane at the point . (Here it is assumed that the area at is regular , i.e. that and are linearly independent .) A normal vector in the point is a vector that is perpendicular to and , e.g. B. the main normal vector given by the cross product and then normalized
Here the vertical lines indicate the Euclidean norm of the vector.
If the area is given implicitly by an equation,
- ,
where is a differentiable function, then is the gradient
a normal vector of the surface in the point (provided that it does not vanish there).
If the area is given as a graph of a differentiable function , then
an upward normal vector at the point . This is obtained by using that the mapping is a parameterization or that the area is given by the equation
is pictured.
Generalizations
The concept of the normal vector can be generalized to
- affine subspaces (generalized levels) in Euclidean spaces of higher dimensions (mathematics) (especially on hyperplanes ),
- Surfaces, hypersurfaces and submanifolds in Euclidean spaces of higher dimensions,
- Surfaces, hypersurfaces and submanifolds of Riemannian manifolds ,
- Non-smooth objects, such as convex bodies and rectifiable sets.
Applications
In the field of computer graphics , normal vectors are used, among other things, to determine whether a surface is facing the user or not in order to exclude the latter from the image calculation ( back-face culling ). They are also required to calculate incidence of light and reflections.