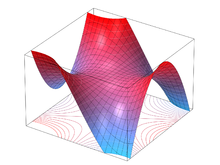
Tangent plane

Tangent plane to a surface

The tangent plane at a point on a surface in three-dimensional space is the plane that best approximates (touches) the surface in the vicinity of the point . It is therefore the two-dimensional correspondence to the tangent of a curve . As in the case of the curve, a tangent plane only exists if the surface is sufficiently "smooth". This applies, for example, to the graphs of differentiable functions of two variables. A surface that has a kink or a point - for example a cone - has no tangent plane at these points. ${\displaystyle P}$ ${\displaystyle F}$ ${\displaystyle P}$

A plane is defined by a point (in this case the point of contact ) and two linearly independent direction vectors or by a point and a normal vector . Depending on how a given surface is described (implicitly, explicitly or parameterized, see below), either direction vectors or a normal vector will be determined. ${\displaystyle P}$

The tangential plane forms the two-dimensional special case of a tangential space of a submanifold of the ${\displaystyle \mathbb {R} ^{n}}$ .

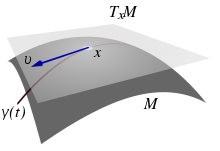
Illustration of the definition. Here the area is called M and the point of contact is called x .

Formal definition

Let it be a regular surface and a point. ${\displaystyle F\subset \mathbb {R} ^{3}}$ ${\displaystyle p_{0}\in F}$

The tangential plane at in the point is the plane through which is spanned by the velocity vectors of paths running through : If the function is a path with , then a point is the tangential plane. Since the tangential plane is two-dimensional, two such paths (in different directions) are sufficient to span the tangential plane. ${\displaystyle F}$ ${\displaystyle p_{0}}$ ${\displaystyle p_{0}}$ ${\displaystyle p}$ ${\displaystyle \gamma \colon (-1,1)\to F}$ ${\displaystyle \gamma (0)=p_{0}}$ ${\displaystyle p_{0}+{\dot {\gamma }}(0)}$

Tangent plane on the graph of a function

Paraboloid

The area is as a graph ${\displaystyle F}$

${\displaystyle F=\{(x,y,z)\in \mathbb {R} ^{3}\mid z=f(x,y)\}}$

given a function of two variables . We are looking for the tangential plane to the surface at a point . If the function is differentiable at this point with the partial derivatives , the first order Taylor polynomial yields ${\displaystyle f}$ ${\displaystyle x,y}$ ${\displaystyle p_{0}=(x_{0},y_{0},f(x_{0},y_{0}))}$ ${\displaystyle f}$ ${\displaystyle (x_{0},y_{0})}$ ${\displaystyle f_{x}(x_{0},y_{0}),\ f_{y}(x_{0},y_{0})}$

${\displaystyle z=f(x_{0},y_{0})+f_{x}(x_{0},y_{0})(x-x_{0})+f_{y}(x_{0},y_{0})(y-y_{0})}$

an equation of the desired tangential plane. The tangent plane is thus the graph of the affine-linear function

${\displaystyle (x,y)\mapsto f(x_{0},y_{0})+f_{x}(x_{0},y_{0})(x-x_{0})+f_{y}(x_{0},y_{0})(y-y_{0})}$.

Example: The area (a paraboloid) is given as a graph of the function with . Be it . With and results ${\displaystyle F}$ ${\displaystyle f}$ ${\displaystyle f(x,y)=x^{2}+2y^{2}}$ ${\displaystyle (x_{0},y_{0})=(3,4)}$ ${\displaystyle f_{x}(x,y)=2x}$ ${\displaystyle f_{y}(x,y)=4y}$

${\displaystyle z=41+6(x-3)+16(y-4)}$ or.

${\displaystyle z=6x+16y-41}$

as the equation of the desired tangent plane in the surface point . ${\displaystyle (3,4,41)}$

Tangential plane to an implicitly given surface

Ellipsoid

In this case the surface is a level surface

${\displaystyle F=\{(x,y,z)\in \mathbb {R} ^{3}\mid f(x,y,z)=0\}}$

given a function of 3 variables. For example, the unit sphere is given by the equation ${\displaystyle f}$

${\displaystyle x^{2}+y^{2}+z^{2}-1=0}$

given. Let it be a point of area d. H. it is . If is differentiable in the point and ${\displaystyle p_{0}=(x_{0},y_{0},z_{0})}$ ${\displaystyle f(x_{0},y_{0},z_{0})=0}$ ${\displaystyle f}$ ${\displaystyle p_{0}}$

${\displaystyle \operatorname {grad} f(p_{0})=(f_{x}(p_{0}),f_{y}(p_{0}),f_{z}(p_{0}))\neq (0,0,0)}$

holds, the tangent plane at the point is given by the equation ${\displaystyle (x_{0},y_{0},z_{0})}$

${\displaystyle f_{x}(p_{0})(x-x_{0})+f_{y}(p_{0})(y-y_{0})+f_{z}(p_{0})(z-z_{0})=0}$

shown. Reason: The vector points in the direction of the greatest increase in and must therefore be a normal vector of the tangential plane sought. ${\displaystyle \operatorname {grad} f(p_{0})}$ ${\displaystyle f}$

Example: The area is an ellipsoid with the equation ${\displaystyle F}$

${\displaystyle f(x,y,z)=x^{2}+2y^{2}+4z^{2}-1=0}$,

what is sought is the tangential plane of at the point . The following applies and the tangent plane that is sought has the coordinate equation ${\displaystyle F}$ ${\displaystyle p_{0}=(x_{0},y_{0},z_{0})=({\tfrac {1}{\sqrt {2}}},0,{\tfrac {1}{\sqrt {8}}})}$ ${\displaystyle \operatorname {grad} f(x,y,z)=(2x,4y,8z)}$

${\displaystyle {\sqrt {2}}(x-{\tfrac {1}{\sqrt {2}}})+{\sqrt {8}}(z-{\tfrac {1}{\sqrt {8}}})=0}$ or.

${\displaystyle x+2z-{\sqrt {2}}=0}$.

Tangential plane of a parameterized surface

Monkey saddle

In this case the area is given by a parametric representation . If the parameter representation is differentiable at a parameter point and the derivative vectors are linearly independent , then ${\displaystyle (x,y,z)={\vec {S}}(u,v)}$ ${\displaystyle {\vec {S}}(u,v)}$ ${\displaystyle (u_{0},v_{0})}$ ${\displaystyle {\vec {S}}_{u}(u_{0},v_{0}),{\vec {S}}_{v}(u_{0},v_{0})}$

${\displaystyle (x,y,z)={\vec {S}}(u_{0},v_{0})+{\vec {S}}_{u}(u_{0},v_{0})(u-u_{0})+{\vec {S}}_{v}(u_{0},v_{0})(v-v_{0})}$

a parametric representation of the tangential plane at the point . ${\displaystyle p_{0}={\vec {S}}(u_{0},v_{0})}$

Example: is a parametric representation of the monkey saddle . With and results for the tangential plane at any point ${\displaystyle {\vec {S}}(u,v)=(u,v,u^{3}-3uv^{2})}$ ${\displaystyle S_{u}(u,v)=(1,0,3u^{2}-3v^{2})}$ ${\displaystyle S_{v}(u,v)=(0,1,-6uv)}$

${\displaystyle {\begin{pmatrix}x\\y\\z\end{pmatrix}}={\begin{pmatrix}u_{0}\\v_{0}\\u_{0}^{3}-3u_{0}v_{0}^{2}\end{pmatrix}}+{\begin{pmatrix}1\\0\\3u_{0}^{2}-3v_{0}^{2}\end{pmatrix}}(u-u_{0})+{\begin{pmatrix}0\\1\\-6u_{0}v_{0}\end{pmatrix}}(v-v_{0})}$.

Note: The example of the monkey saddle shows that a surface can be represented in several ways: 1) parameterized as introduced here, 2) as a graph of the function and finally 3) implicitly through . ${\displaystyle f(x,y)=x^{3}-3xy^{2}}$ ${\displaystyle f(x,y,z)=x^{3}-3xy^{2}-z=0}$

Intersection of a tangent plane with the surface

There are surfaces that are near a point on one side of the tangent plane at that point. For example: paraboloid and ellipsoid (see above) or cylinder. However, it is also possible that the surface lies in the vicinity of a point on both sides of the tangential plane at this point. E.g. monkey saddle or hyperbolic paraboloid . If the Gaussian curvature in a surface point is not zero, the following applies: with positive Gaussian curvature the first case (surface on one side) and with negative Gaussian curvature the second case (surface on both sides) occurs. If the Gaussian curvature is zero, both cases are possible. For example: cylinder everywhere or monkey saddle in the zero point.

Applications

Wherever the description of a surface is too complicated for calculations, tangent planes are used as a substitute for the given surface, e.g. B. at

• the determination of points of the intersection curve of two surfaces ( Newton method ),
• the determination of outline points of a surface: the projection direction lies in the tangential plane of an outline point,
• Images ( projections of surfaces onto a plane, as is necessary for maps, for example ).

literature

• Meyberg & Vachenauer: Higher Mathematics 1. Springer-Verlag, Berlin 1995, ISBN 3-540-59188-5 , pp. 380, 392, 468
• Do Carmo: Differential geometry of curves and surfaces, Vieweg-Verlag, 1983