Submanifold of ℝ ⁿ

In mathematics , submanifolds of ${\displaystyle \mathbb {R} ^{n}}$ (also: submanifolds of Euclidean space ) are a term from analysis and differential geometry . Since the submanifolds are subsets of a Euclidean space , they inherit many properties from it, such as the ability to measure distances. However, every submanifold can also be viewed as an abstract differentiable manifold (without surrounding space). The equivalence of the two perspectives is ensured by Whitney's embedding theorem .

Selected examples in which submanifolds of the play a role are: ${\displaystyle \mathbb {R} ^{n}}$

• Optimization under constraints
• Mechanical systems with constraints
• Algebro differential equation systems , for example in numerical network analysis in electrical engineering

In all these applications, the amount of the observed points is from the outset to a subset of the restricted, locally by diffeomorphisms of a number of fields with can be mapped. This subset is called the -dimensional submanifold of the . With the help of the diffeomorphisms one can calculate on the submanifold in the differential geometric sense just as in areas of the . ${\displaystyle M}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle \mathbb {R} ^{m}}$ ${\displaystyle 0\leq m\leq n}$ ${\displaystyle M}$ ${\displaystyle m}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle \mathbb {R} ^{m}}$

Mostly the amount is described by constraints. That is, contains precisely those points which with a given continuously differentiable function with the equation ${\displaystyle M}$ ${\displaystyle M}$ ${\displaystyle x}$ ${\displaystyle f\colon \mathbb {R} ^{n}\rightarrow \mathbb {R} ^{n-m}}$ ${\displaystyle 0<m<n}$

${\displaystyle f(x)=0}$

fulfill. Also, even demanded that a regular value of is, so the Jacobian of all points the maximum rank has. ${\displaystyle 0}$ ${\displaystyle f}$ ${\displaystyle Df(x)}$ ${\displaystyle f}$ ${\displaystyle x\in M}$ ${\displaystyle \left.n-m\right.}$

The last condition ensures the applicability of the theorem about implicit functions. This means that for each point there is an environment of in which the points are already clearly parameterized by coordinates. The image that projects onto the coordinates required for parameterization is an example of a map image and is the associated map area . Since there is a map image for each point , you can completely cover with the associated map areas. A lot of such maps, with whose map areas one can cover, is an example of an atlas . ${\displaystyle {\bar {x}}\in M}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle U_{\bar {x}}}$ ${\displaystyle {\bar {x}}}$ ${\displaystyle x\in U_{\bar {x}}\cap M}$ ${\displaystyle m}$ ${\displaystyle x\in U_{\bar {x}}\cap M}$ ${\displaystyle U_{\bar {x}}\cap M}$ ${\displaystyle {\bar {x}}\in M}$ ${\displaystyle M}$ ${\displaystyle M}$

With the help of the map images you can calculate locally and in . This motivates that the natural number is called the dimension of and is called the -dimensional submanifold of . ${\displaystyle M}$ ${\displaystyle \mathbb {R} ^{m}}$ ${\displaystyle m}$ ${\displaystyle M}$ ${\displaystyle M}$ ${\displaystyle m}$ ${\displaystyle \mathbb {R} ^{n}}$

example

Map areas and projections as map images for the einim. Unity sphere

The unit sphere im is described with the continuously differentiable function by the equation . The Jacobi matrix has one for with its maximum rank. So is ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle f(x):=\|x\|^{2}-1}$ ${\displaystyle f(x)=0}$ ${\displaystyle Df(x)=2x^{T}}$ ${\displaystyle x\in \mathbb {R} ^{n}}$ ${\displaystyle \|x\|=1}$

${\displaystyle M:=\{x\in \mathbb {R} ^{n}\mid \|x\|^{2}-1=0\}}$

an (n - 1) - dimensional submanifold of the . At least one coordinate is not equal to zero in each point . For you can with the crowd ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle {\bar {x}}\in M}$ ${\displaystyle {\bar {x}}_{k}}$ ${\displaystyle {\bar {x}}_{k}>0}$ ${\displaystyle U_{\bar {x}}^{k+}=\{x\in \mathbb {R} ^{n}\mid x_{k}>0\}}$

${\displaystyle M\cap U_{\bar {x}}^{k+}=\{x\in \mathbb {R} ^{n}\mid \|x\|=1,\,x_{k}>0\}}$

use as map area and for with the crowd ${\displaystyle {\bar {x}}_{k}<0}$ ${\displaystyle U_{\bar {x}}^{k-}=\{x\in \mathbb {R} ^{n}\mid x_{k}<0\}}$

${\displaystyle M\cap U_{\bar {x}}^{k-}=\{x\in \mathbb {R} ^{n}\mid \|x\|=1,\,x_{k}<0\}}$.

The illustrations

${\displaystyle \phi _{k+}\colon M\cap U_{\bar {x}}^{k+}\to \mathbb {R} ^{n-1}}$

${\displaystyle \phi _{k-}\colon M\cap U_{\bar {x}}^{k-}\to \mathbb {R} ^{n-1}}$

With

${\displaystyle \phi _{k+}(x)=\phi _{k-}(x)=(x_{1},\ldots ,x_{k-1},x_{k+1},\ldots ,x_{n})}$

are then suitable as maps for these areas.

This procedure is easiest to illustrate for the one-dimensional unit sphere im . In the picture opposite, the four map areas are shown as thick, solid lines. The union of the map areas covers the entire unit sphere, so these maps together form an atlas. The flatteners belonging to the map areas are indicated by a small arrow. The images of the map areas are dashed in thick lines. ${\displaystyle \mathbb {R} ^{2}}$

For the two-dimensional unit sphere in , you already need two coordinates for the unique parameterization of the points in the map areas. For example one chooses for the quantity and as a map image . ${\displaystyle \mathbb {R} ^{3}}$ ${\displaystyle {\bar {x}}_{1}>0}$ ${\displaystyle U_{\bar {x}}:=\{x\in \mathbb {R} ^{3}\mid x_{1}>0\},}$ ${\displaystyle \phi (x)=(x_{2},x_{3})}$

The Möbius strip also has local properties like a region of and should therefore also be able to be described as a two-dimensional differentiable submanifold of . If the Möbius strip could be represented as the archetype of a regular value of a continuously differentiable function , then the continuous gradient of this function standing perpendicular to it would have to point in one direction everywhere (as e.g. pointing away from the front). However, this does not work because the Möbius strip has no front or back. Therefore the definition of the differentiable submanifold of the something has to be made more general. ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle \mathbb {R} ^{3}}$ ${\displaystyle f\colon \mathbb {R} ^{3}\rightarrow \mathbb {R} }$ ${\displaystyle M}$ ${\displaystyle \mathbb {R} ^{n}}$

Definition of a submanifold of Euclidean space

A set is a -dimensional -time continuously differentiable submanifold of , if for every point there is a -surrounding and a -time continuously differentiable function with regular value 0, so that . ${\displaystyle M\subset \mathbb {R} ^{n}}$ ${\displaystyle m}$ ${\displaystyle k}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle {\bar {x}}\in M}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle U_{\bar {x}}}$ ${\displaystyle k}$ ${\displaystyle f_{\bar {x}}\colon U_{\bar {x}}\rightarrow \mathbb {R} ^{n-m}}$ ${\displaystyle f_{\bar {x}}^{-1}(\{0\})=M\cap U_{\bar {x}}}$

Important statements

Equivalent to this is: A set is a -time continuously differentiable submanifold of if and only if there is a local flattener for every point , i.e. i.e. to exist an environment and a diffeomorphism such that applies to all : if and only if . ${\displaystyle M\subset \mathbb {R} ^{n}}$ ${\displaystyle k}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle {\bar {x}}\in M}$ ${\displaystyle {\bar {x}}}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle U_{\bar {x}}}$ ${\displaystyle C^{k}}$ ${\displaystyle f\colon U_{\bar {x}}\rightarrow f(U_{\bar {x}})\subset \mathbb {R} ^{n}}$ ${\displaystyle x\in U_{\bar {x}}}$ ${\displaystyle f_{m+1}(x)=\ldots =f_{n}(x)=0}$ ${\displaystyle x\in M}$

A regular parametric representation is a continuously differentiable function that maps an area of the and whose Jacobi matrix has the maximum rank for each parameter . ${\displaystyle g}$ ${\displaystyle \Omega }$ ${\displaystyle \mathbb {R} ^{m}}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle (n,m\in \mathbb {N} ,m<n)}$ ${\displaystyle Dg(p)}$ ${\displaystyle p\in \Omega }$ ${\displaystyle m}$

If a local flattener is a manifold , then it is a regular parametric representation that parameterizes at least the part of . In this case, projected with the essential components of the local flat-maker. ${\displaystyle f_{\bar {x}}\colon U_{\bar {x}}\rightarrow f(U_{\bar {x}})}$ ${\displaystyle M}$ ${\displaystyle g:={\Big (}\mathrm {pr} _{1:m}f_{\bar {x}}|(U_{\bar {x}}\cap M){\Big )}^{-1}}$ ${\displaystyle U_{\bar {x}}\cap M}$ ${\displaystyle M}$ ${\displaystyle \mathrm {pr} _{1:m}\colon \mathbb {R} ^{n}\rightarrow \mathbb {R} ^{m}}$ ${\displaystyle \mathrm {pr} _{1:m}(x)=(x_{1},\ldots ,x_{m})}$

Example of an immersion whose full image no submanifold of is ${\displaystyle \mathbb {R} ^{n}}$

Manifolds can also be defined locally using regular parametric representations: If a regular parametric representation is arbitrary, then there is an environment of , so that the image of under represents a differentiable submanifold of . ${\displaystyle g\colon \Omega \rightarrow \mathbb {R} ^{n}}$ ${\displaystyle p\in \Omega }$ ${\displaystyle U_{p}\subset \Omega }$ ${\displaystyle p}$ ${\displaystyle g(U_{p})\subset \mathbb {R} ^{n}}$ ${\displaystyle U_{p}}$ ${\displaystyle g}$ ${\displaystyle \mathbb {R} ^{n}}$

example

The immersion illustrated on the right with is an example that the above statement is not necessarily generalizable to the full picture of an immersion (even if, as in this example, the immersion is injective). The set is locally not diffeomorphic to an interval of the real axis around the point and therefore does not represent a one-dimensional submanifold of the . ${\displaystyle g\colon (-\pi /2,3\pi /2)\rightarrow \mathbb {R} ^{2}}$ ${\displaystyle g(p):={\big (}2\cos(p),\sin(2p){\big )}}$ ${\displaystyle M:=g{\big (}(-{\frac {\pi }{2}},3{\frac {\pi }{2}}){\big )}}$ ${\displaystyle (0,0)}$ ${\displaystyle \mathbb {R} ^{n}}$

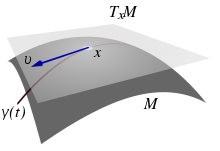
Tangential vectors / tangent space / tangential bundle

Tangential vector at in defined as the velocity vector of a curve through and tangential space at the point ${\displaystyle M}$ ${\displaystyle x\in M}$ ${\displaystyle \gamma }$ ${\displaystyle x}$ ${\displaystyle x}$

Let be a -dimensional differentiable submanifold of and . A vector is called a tangent vector at at the point if there is a differentiable curve with and . ${\displaystyle M}$ ${\displaystyle m}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle x\in M}$ ${\displaystyle v\in \mathbb {R} ^{n}}$ ${\displaystyle M}$ ${\displaystyle x}$ ${\displaystyle \gamma \colon (-\varepsilon ,\varepsilon )\rightarrow M}$ ${\displaystyle \left.\gamma (0)=x\right.}$ ${\displaystyle {\dot {\gamma }}(0)=v}$

If one looks at the trajectory of a particle moving on the submanifold , then this particle is currently passing the point of interest with speed . ${\displaystyle t\in (-\varepsilon ,\varepsilon )\mapsto \gamma (t)}$ ${\displaystyle M}$ ${\displaystyle t=0}$ ${\displaystyle x}$ ${\displaystyle v}$

The set of all tangent vectors an in the point is a -dimensional linear space and is called the tangent space in in the point . ${\displaystyle T_{x}M}$ ${\displaystyle M}$ ${\displaystyle x\in M}$ ${\displaystyle m}$ ${\displaystyle M}$ ${\displaystyle x}$

By definition, the submanifold can be represented in a neighborhood of the point as a regular zero of a function . Let be any continuously differentiable curve with . Since this runs on the manifold, it fulfills the equation . Deriving after at the point gives , from which it follows: ${\displaystyle U_{\bar {x}}}$ ${\displaystyle {\bar {x}}\in M}$ ${\displaystyle f\colon U_{\bar {x}}\rightarrow \mathbb {R} ^{n-m}}$ ${\displaystyle \gamma \colon (-\varepsilon ,\varepsilon )\rightarrow U_{\bar {x}}\cap M}$ ${\displaystyle \gamma (0)={\bar {x}}}$ ${\displaystyle f(\gamma (t))=0}$ ${\displaystyle t}$ ${\displaystyle t=0}$ ${\displaystyle Df(\gamma (t)){\dot {\gamma }}(t)|_{t=0}=0}$

The tangential space is the core of the Jacobi matrix that belongs to it , that is, it applies . ${\displaystyle T_{x}M}$ ${\displaystyle f}$ ${\displaystyle Df({\bar {x}})}$ ${\displaystyle T_{\bar {x}}M=\{v\in \mathbb {R} ^{n}\mid Df({\bar {x}})v=0\}}$

If you have given a (local) regular parameter representation that maps a parameter point in , the tangential space an in can also be represented as a full picture of the associated Jacobi matrix : ${\displaystyle g\colon \Omega \subset \mathbb {R} ^{m}\rightarrow M}$ ${\displaystyle p\in \Omega }$ ${\displaystyle x\in M}$ ${\displaystyle M}$ ${\displaystyle x}$ ${\displaystyle Dg(p)}$

${\displaystyle T_{x}M=\{Dg(p)u\mid u\in \mathbb {R} ^{m}\}.}$

The relation that assigns all tangent vectors to to each point at this point is called the tangent bundle of . ${\displaystyle TM:=\{(x,v)\in M\times \mathbb {R} ^{n}\mid v\in T_{x}M\}}$ ${\displaystyle x\in M}$ ${\displaystyle M}$ ${\displaystyle M}$

Let be an at least twice continuously differentiable submanifold of and arbitrary. A local representation of can be constructed from a local representation of in an environment of : ${\displaystyle M}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle {\bar {x}}\in M}$ ${\displaystyle M\cap U_{\bar {x}}=\{x\in U_{\bar {x}}\mid f(x)=0\}}$ ${\displaystyle M}$ ${\displaystyle U_{\bar {x}}}$ ${\displaystyle {\bar {x}}}$ ${\displaystyle TM}$

${\displaystyle TM\cap (U_{\bar {x}}\times \mathbb {R} ^{n})=\{(x,v)\in U_{\bar {x}}\times \mathbb {R} ^{n}\mid f(x)=0{\text{ und }}Df(x)v=0\}.}$

This means that there is a -dimensional (at least once) continuously differentiable submanifold of (in the sense of the usual identification of the with the ). ${\displaystyle TM}$ ${\displaystyle 2m}$ ${\displaystyle \mathbb {R} ^{2n}}$ ${\displaystyle \mathbb {R} ^{n}\times \mathbb {R} ^{n}}$ ${\displaystyle \mathbb {R} ^{2n}}$

literature

• Konrad Königsberger: Analysis 2 , Springer-Verlag, Berlin / Heidelberg, 2000, ISBN 3-540-43580-8