Möbius strip

Möbius strip , Möbius loop or Möbius'sches band describes a surface that has only one edge and one side. It cannot be orientated , that is, one cannot distinguish between below and above or between inside and outside.
The Möbius strip was described independently in 1858 by the Göttingen mathematician and physicist Johann Benedict Listing and the Leipzig mathematician and astronomer August Ferdinand Möbius .
description
A Möbius strip is easy to make by gluing a long strip of paper together with both ends in a ring, but twisting one end by 180 ° before gluing it together. Such Möbius strips have a center line that cannot occupy a circle - unless the strip is locally stretched. The shape that such a band can assume unstretched is completely described by the course of the center line. Möbius strips, whose center line is a circle even in the relaxed state, cannot be made from a straight two-dimensional strip of paper - they have unevenly shaped sub-elements along their circumference, from which they can be thought of as being assembled.
Möbius strips are chiral .
The Möbius strip merges into itself in such a way that if you start coloring the surface on one of the apparently two sides, you have colored the entire object in the end.
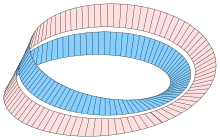
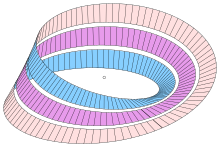
Other interesting effects are created if you draw a center line or two lines parallel to the center line on the tape and cut the tape along this line (s), i.e. it appears to be halved or thirds. In the first case, i.e. when cutting along the center line, a double-twisted ring (twisted by 720 °) with two sides and two edges is created. In the second case, the outer thirds create a twofold twisted ring as in the first case, the middle third results in a new Möbius strip hanging in it. This game can be continued with any number of small divisions: if you “quarter” the ribbon, two double-twisted ribbons are created which are not only interlocked, but also looped around each other more often; If you “fifth” it, the result is the same figure with an additional inner Möbius strip that hangs in the two rings; If you “sixth” the band, you get two rings that are wrapped around each other twice and are wrapped around twice by another ring, the outer and the two inner rings being interchangeable as required; If you "seventh" it again, a Möbius strip is added, which hangs in the three rings, etc. If the denominator of the fraction into which the strip is apparently divided is straight , so you get rings; if it is odd, a Möbius strip is also looped through the rings.
From a mathematical point of view, the Möbius strip is a non-orientable manifold . Another area that falls into this category is the Klein bottle ; a Klein bottle can be divided into two parts so that two Möbius strips are created from it.
In the nature
- Charged particles trapped in the earth's magnetic field can move on a Möbius strip.
- The cyclic protein Kalata B1, active ingredient of the Oldenlandia plant . O. affinis , as a natural remedy z. B. for the induction of labor, has a Möbius topology.
In art and literature

There are famous representations of the Möbius strip in art . B. by M. C. Escher (Möbius volume I and II, 1963) and more recently by Gideon Möbius-Sherman . The Argentine feature film Moebius also deals with the subject. The Möbius strip is also discussed in the literature: The structure of John Barth's short story series Lost in the Funhouse (Eng. "Ambrose im Juxhaus") is based on the infinity or repetition principle (e.g. missing center) of the Möbius strip. A Möbius strip is also supplied with the book, which reflects postmodern literature approaches (“frame-tale”). It is labeled: "Once upon a time there was a story that began once upon a time ...". This form of self-reference is typical of so-called strange loops . In his poem Topologik , the lyricist Erich Fried refers to the Möbius strip: “I have created a Möbius heart that cuts into hopeless strips.” From the 1930s onwards, Max Bill created numerous sculptures that correspond to the visual representations of the Möbius strip : B. Infinite Loop (1935/37), Continuity (Lake Zurich; 1947, destroyed 1948) or Infinite Loop (Stadtgarten Essen, on Hohenzollernstrasse; 1974). However, his sculpture Continuity (1986) does not represent a Möbius strip, contrary to popular belief.
The Möbius strip also plays an important role in the Necroscope series of novels by the English author Brian Lumley , which has been in existence since 1986 . It is the symbol of some characters, but especially important for the main character Harry Keogh. He learns the ability to travel through time with the help of the so-called Möbius continuum, which behaves similar to the Möbius strip.
The Möbius strip is also a theme in the Perry-Rhodan series and here forms the three-dimensional model description for the two sides of the -dimensional universe (arresum and paresum).
Lars Gustafsson develops the Möbius strip further in his novel Frau Sorgedahl's Beautiful White Arms into a Möbius time bottle in which we are trapped. Outside of our life there is nothing.
In the manga series Angel Sanctuary , the fate of the high angel Alexiel and the constant rebirth of his soul in human bodies, for which a cruel and bloody fate is predetermined, is compared with a Möbius loop.
In 2011, published in German language novel The Map and the Territory of Michel Houellebecq , a Moebius strip is engraved on the grave plate of the fictional character Michel Houellebecq.
In 2011, the robotics student Aaron Hoover at the University of California, Berkeley, created a Möbius gearbox as a technical gimmick using 3D printing .
The Möbius chess is a variant of the cylinder chess in which one also thinks of twisting the playing field when "connecting" the long sides.
In the video game Mario Kart 8 , the Mario Circuit racetrack represents a Möbius tape. The 8 in the logo also shows a Möbius tape.
Möbius scarves have also been designed in fashion.
In the play Solaris based on Stanislaw Lem by Bettina Bruinier and Katja Friedrich at the Münchner Volkstheater (2011), a Möbius strip on which a model car drives is an important part of the staging (stage design: Markus Karner).
The logos of Commerzbank and the German building cleaning trade show a Möbius strip.
The GDR Avantgarde Band AG. Geige dedicated a song to the Möbius band on the 1989 album Trickbeat.
In technology
mechanics
- The belt of a belt drive can be designed as a Möbius belt . On gearboxes with pulleys with parallel axes, it makes it easier to pull the belt on and off. The 180 ° transposition should then in the empty strand lie, can be guided in the longitudinal center of the belt gently with two rollers in its lateral position. As a result of this twisting, the zones near the belt edge are stretched somewhat more. If the flutter changes, “both sides of the belt” come into engagement and the belt material is bent in one direction during one revolution and in the opposite direction during the next.
Consumer electronics
- With the Tefifon , the sound tape scanned by a pick-up needle could be implemented as a Möbius tape, but this has proven to be impractical.
Electrical engineering
- The circuitry analog of a Möbius strip is a ring counter with an inversion ( Johnson counter ): A bit sequence reaches the initial state after two cycles, so memory cells can be used to count up to; Counting pulses in rapid succession.
- As a compact resonator with the resonance frequency of half of the identical linear coils.
- As an induction-free resistor, which is also known as the Möbius resistor .
physics
- As a superconductor with a high transition temperature.
- The stellarator is a type of nuclear fusion reactor in which the plasma is brought into a Moebius-shaped path by appropriately shaped field coils.
chemistry
nanotechnology
- As molecular motors.
- As a graphene tape (nano-graphite) with novel electronic properties such as helical magnetism.
In math
Parametric representation
The Möbius strip can be drawn as a surface using the following parameter representation :
with and . This creates a Möbius strip with a width of 1, the center line of which coincides with the unit circle of the xy plane . The corner has its apex in the center; as it changes, the variation of leads to the surface that spans between the single edge. As can be easily seen in the picture on the right, it is not a Möbius strip to be made from a strip of paper - in the horizontal part the sub-elements resemble symmetrical trapezoids .
With the help of cylindrical coordinates , the Möbius strip can go through
to be discribed.
topology
The topology offers a mathematical way of producing a Möbius strip by gluing the ends of a paper strip together in opposite directions. There a Möbius strip is defined as the quotient space of the square , whereby two opposite sides are identified by the equivalence relation for each other . The diagram opposite illustrates this.
The Möbius strip is a compact topological manifold of dimension 2.
geometry
In the area of differential geometry , a Möbius strip is understood as a non-orientable surface with a hole . It can be embedded in the. The tape is the standard example of a non-orientable surface. The Möbius strip allows for a differentiable structure . However, it is not a Riemannian surface , since non-orientable surfaces do not allow complex structures .
The paper model of the Möbius strip discussed in the first section can be developed onto the plane . Therefore the Gaussian curvature of such Möbius strips disappears . As shown in the section on the parameterization of a Möbius strip, there are also Möbius strips that cannot be developed on the plane. Thus, according to the theorema egregium, not all Möbius strips are isometrically isomorphic to one another .
Calculus of variations
New findings on the mathematical description of a Möbius strip were published in 2007 by the scientists EL Starostin and GHM van der Heijden . In particular, they have mathematically calculated the shape that a Möbius strip made from a strip strives to adopt by itself in order to assume the lowest energy state.
literature
- Rainer Herges: Möbius, Escher, Bach - The infinite bond in art and science. In: Naturwissenschaftliche Rundschau . 58, 6, 2005, pp. 301-310.
- Clifford A. Pickover: The Möbius Strip: Dr. August Möbius's Marvelous Band in Mathematics, Games, Literature, Art, Technology, and Cosmology. New York 2006.
Web links
- Eric W. Weisstein : Moebius Strip . In: MathWorld (English).
- Möbius strip - a web page with movies (English).
- Tie the Möbius strip (PDF; 271 kB; English).
Individual evidence
- ^ JJ O'Connor, EF Robertson: Johann Benedict Listing. Biography. In: mathshistory.st-andrews.ac.uk. Retrieved April 10, 2020.
- ↑ a b Holger Dambeck: Numerator. Mystery of the Möbius strip solved. In: Spiegel.de . July 19, 2007, accessed April 10, 2020.
- ↑ SC Hsu, PM Bellan: Study of magnetic helicity injection via plasma imaging using a high-speed digital camera . In: IEEE Transactions on Plasma Science . tape 30 , no. 1 , February 2002, p. 10-11 , doi : 10.1109 / TPS.2002.1003898 .
- ^ VB Gerritsen: The protein with a topological twist. In: Protein Spotlight 20th Issue 20, March 2002, accessed April 10, 2020.
- ↑ E.g. Anne Schloen: The renaissance of gold. Gold in 20th Century Art. (PDF; 1.8 MB). In: Uni-Koeln.de. Dissertation at the Philosophical Faculty of the University of Cologne, Chapter 2.2. Cologne 2006, accessed on April 10, 2020.
- ↑ Angel Sanctuary . Volume 3. Carlsen Comics, 1995, p. 92.
- ↑ Charlie Sorrel: Real Möbius Gear Will Melt Your Mind. In: Wired.com. July 4, 2011, accessed April 10, 2020 .
- ↑ Lavender witch: Möbius scarf. In: Lavendelhexe.net. December 31, 2009, accessed April 10, 2020 .
- ^ Anne Steiner: The production at the Volkstheater - Bettina Bruinier (direction). In: Solaris after Stanislaw Lem - materials for staging. November 27, 2011.
- ↑ Patent DE400399 : Device for the photographic recording of sounds and their reproduction. Published on August 6, 1924 , Applicant: Dr. Lee de Forest.
- ↑ NTZ. Issue 1, Jan. 1964, pp. 24-34.
- ^ W. Hilberg: A 500 Mc Twisted Ring Counter Whose Resolution Is Limited By Gate Switching Speed Only . In: Nuclear Instruments and Methods . tape 33 , 1965, pp. 322-324 , doi : 10.1016 / 0029-554X (65) 90064-9 .
- ↑ JM Pond: Mobius dual-mode resonators and bandpass filters . In: IEEE Trans. Microwave Theory and Tech. tape 48 , 2000, pp. 2465-2471 , doi : 10.1109 / 22.898999 .
- ↑ Patent US3267406 : Non-inductive electrical resistor. Published August 16, 1966 , Inventor: Richard L. Davis.
- ^ R. Pérez-Enríquez: A Structural Parameter for High Tc Superconductivity from an Octahedral Moebius Strip in RBaCuO: 123 type Perovskites . In: Rev. Mex. F sharp. 48, Supplement 1, March 2002, pp. 262-267 , arxiv : cond-mat / 0308019 .
- ↑ Gaston R. Schaller, Rainer Herges: Möbius molecules with twists and writhes. In: Chem. Comm. 2013, pp. 1254-1260.
- ^ Oleg Lukin, Fritz Vögtle : Knotting and Threading of Molecules: Chemistry and Chirality of Molecular Knots and Their Assemblies . In: Angew. Chem. Int. Ed. tape 44 , 2005, pp. 1456-1477 , doi : 10.1002 / anie.200460312 .
- ↑ Atsushi Yamashiro, Yukihiro Shimoi, Kikuo Harigaya, Katsunori Wakabayashi: Novel electronic states in graphene ribbons - competing spin and charge orders . In: Physica E . tape 22 , 2006, p. 688-691 , doi : 10.1016 / j.physe.2003.12.100 , arxiv : cond-mat / 0309636v1 .
- ^ Manfredo Perdigão do Carmo: Differential Geometry of Curves and Surfaces. Prentice-Hall, Upper Saddle River, NJ 1976, ISBN 0-13-212589-7 , p. 106 ( PDF; 18.7 MB ).
- ↑ Vladimir G. Ivancevic, Tijana T. Ivancevic: Applied Differential Geometry. A Modern Introduction . World Scientific, 2007, ISBN 978-981-270-614-0 , pp. 18 .
- ↑ Möbius strip . In: Guido Walz (Ed.): Lexicon of Mathematics . 1st edition. Spectrum Academic Publishing House, Mannheim / Heidelberg 2000, ISBN 3-8274-0439-8 .
- ↑ EL Starostin, GHM van der Heijden: The shape of a Möbius strip. 2007, abstract. In: Nature Materials ( PDF; 442 kB ).




















![(x, y) \ in [0.1] \ times [0.1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6d95b074f61bc9fac67a16e74107ccf025eee4e)


