Klein bottle

Two-dimensional representation of the Klein bottle as immersion in three-dimensional space

Structure of a three-dimensional Klein bottle

The Klein bottle (also known as the Klein tube ) was first described in 1882 by the German mathematician Felix Klein . It is an example of a non-orientable surface . In colloquial terms, it has the property that inside and outside cannot be differentiated, or to put it another way, that it has only one side that is inside and outside at the same time . Therefore, as with the Möbius strip , no continuous normal vector can be defined on the Klein surface . In contrast to the Möbius strip, this surface has no edge .

construction

You start with a square and glue the corners and edges together with the appropriate colors so that the arrows match each other. This is shown in the following sketch. In formal terms, Klein's bottle is described by the quotient topology of the square with edges that satisfy the following relations: for and for . ${\displaystyle [0,1]\times [0,1]}$ ${\displaystyle (0,y)\sim (1,y)}$ ${\displaystyle 0\leq y\leq 1}$ ${\displaystyle (x,0)\sim (1-x,1)}$ ${\displaystyle 0\leq x\leq 1}$

The square is a fundamental polygon of Klein's bottle.

Note that this description means "gluing" in an abstract sense that seeks to construct the three-dimensional Klein bottle with intersecting edges. In fact, the Klein bottle has no crossed edges. Regardless of this, it is a way of illustrating this object in its construction.

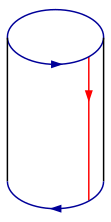
Glue the red arrows of the square together (left and right edges) so that you get a cylinder. Pull the cylinder apart a little and continue to glue the ends together so that the arrows fit on the circle. The circular surface of one cylinder surface is pushed through that of the other. Note that this process leads to the crossing of edges. This is known as the immersion of the Klein bottle in three-dimensional space.

• 

  Step 1

• 

  step 2

• 

  step 3

• 

  Step 4

• 

  Step 5

• 

  Step 6

If the Klein bottle is embedded in the four-dimensional real space, self-penetration can be avoided. This is done clearly as follows: Take the immersion shown above in the three-dimensional space and leave the fourth coordinate at zero for the time being. In the vicinity of the self-penetration, the value of the fourth coordinate for one of the (local) components is continuously increased to one and then lowered again. The fourth coordinate can be graphically illustrated by choosing a different color.

Description in three-dimensional space

Glass-blown Klein bottle

Like the Möbius strip , the Klein bottle is a two-dimensional, differentiable manifold that cannot be oriented. In contrast to the Möbius strip, the Klein bottle cannot be embedded in three-dimensional Euclidean space without self-penetration . So it cannot be embedded in it , it can only be immersed in it. Without self-penetration, however, embedding in and in higher-dimensional spaces is possible. ${\displaystyle \mathbb {R} ^{3}}$ ${\displaystyle \mathbb {R} ^{3}}$ ${\displaystyle \mathbb {R} ^{4}}$

Half of a Klein bottle, according to the parameterization for . ${\displaystyle 0<u<2\pi ,0<v<\pi }$

An immersed Klein bottle can be represented for and by the following equations in : ${\displaystyle 0\leq u<2\pi }$ ${\displaystyle 0\leq v<2\pi }$ ${\displaystyle \mathbb {R} ^{3}}$

${\displaystyle {\begin{aligned}&x=b\,(1-\sin(u))\,\cos(u)+r\,\cos(v)\,(2\,e^{-(u/2-\pi )^{2}}-1)\\&y=r\,\sin(v)\\&z=h\,\sin(u)+0.5\,r\,\sin(u)\cos(v)\,e^{-(u-3\pi /2)^{2}},\end{aligned}}}$

where is. is the approximate width, approximate height of the figure. Usual values: , . ${\displaystyle r=2\,-\cos(u)}$ ${\displaystyle b}$ ${\displaystyle h}$ ${\displaystyle b=2}$ ${\displaystyle h=6}$

Note: The Klein bottle can be divided in such a way that two Möbius strips are created from it (see the illustration on the right).

Topological properties

The fundamental group of the Klein bottle made the presentation

${\displaystyle \pi _{1}(K)=\langle a,b|abab^{-1}=1\rangle }$.

The homology groups are

${\displaystyle H_{0}(K)=\mathbb {Z} ,H_{1}(K)=\mathbb {Z} \oplus \mathbb {Z} /2\mathbb {Z} ,H_{2}(K)=0}$.

The Klein bottle is the non-orientable closed surface of gender 2.

There is a 2-petalled overlay of the Klein bottle by the torus .

Web links

Commons : Kleinsche Bottle  - collection of images, videos and audio files

• The Banchoff-Klein bottle on spass-mit-mathematik.de
• "Small bottles made of glass" at experimentis.de
• Beekeeper Peter: Mathematicians crochet four-dimensional wool hats . ( Memento from March 17, 2003 in the Internet Archive ) Internet presence of the PM magazine
• Bouteille de Klein (French, good pictures) at mathcurve.com
• Construction of the Klein bottle as a video on YouTube
• www.klein-bottle-film.com : Kleinsche bottle animation from 2010: Including a car ride through the Kleinsche bottle and the original description by Felix Klein - video on YouTube

Individual evidence

1. ↑ Eric W. Weisstein : Genus . In: MathWorld (English).