Quotient topology
The quotient topology (also called identification topology ) is a term from the mathematical sub-area of topology . This topology arises clearly when points are "glued together", i. H. identifies two previously different points as one and the same point. Such points are determined by means of equivalence relations . This is generally done to derive new topological spaces from existing ones. For a generalization of this construction see the article final topology .
definition
Let it be a topological space and a surjective mapping of sets . Then the quotient topology induced by is that in which a subset is open if and only if the archetype is open.
properties
- As a direct consequence of the definition, the mapping is continuous.
- The quotient topology is the finest topology for which the mapping is continuous.
- If the quotient topology is provided, a quotient mapping is : If there is another topological space and a mapping of the underlying sets, then continuous if and only if is continuous (universal property of the quotient topology):
Important special cases
- If an equivalence relation is in a topological space, the set of equivalence classes is usually given the quotient topology induced by the canonical mapping without further mentioning .
- If, in particular, there is a topological group and a subgroup of , the homogeneous spaces and are provided with the quotient topology.
- Combining a subspace to a point: If a topological space and a subset of , then denotes the set of equivalence classes with regard to the equivalence relation, in which two points are called equivalent if they are equal or both are in. The image is outside of injective and the image of is a single point.
Examples
- Let it be the unit interval and the unit circle. Then that's through the picture
- induced quotient topology equal to the subspace topology of as a subset of .
- If the unit interval is and , then the space created by joining together to a point is homeomorphic to the circular line . This is essentially the same as the first example, but there the target set and the mapping were already given explicitly; here it was only created through the implicit equivalence relation when merging.
- The homogeneous space is also homeomorphic to the circular line
- In contrast to this, the space that is obtained when the subset of is collapsed to form a point, graphically speaking, consists of countable infinite circles that are glued together at a point.
- If there is a complete ring expansion , the quotient topology induced by the induced continuous spectrum mapping is identical to the Zariski topology in this area.
literature
- Klaus Jänich : Topology ( Springer textbook ). 8th edition. Springer, Berlin et al. 2005, ISBN 3-540-21393-7 .
- Boto von Querenburg : Set theoretical topology (= Springer textbook ). 3rd, revised and expanded edition. Springer, Berlin et al. 2001, ISBN 3-540-67790-9 .










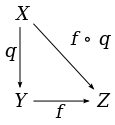










![X = [0.1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/96de4495b54d28b3439ca59802d8730adcb3a588)











