Fundamental group

This article covers the fundamental group in algebraic topology. The fundamental group of a graph of groups is explained there.

The fundamental group is used in algebraic topology to investigate geometric objects or topological spaces . A fundamental group can be assigned to each topological space. However, it is itself an object from algebra and can also be examined using its methods. If two topological spaces have different fundamental groups, one concludes that the two spaces are topologically different, that is, not homeomorphic . Henri Poincaré was the first to introduce the concept of the fundamental group in 1895.

Clear explanation using the example of the torus

A contractible loop on the torus

Two non-contractible loops on the surface of the torus

Linking two loops on the torus

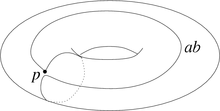
First, the idea of ​​the fundamental group should be explained using an example: The (two-dimensional) torus is considered as a topological space and a base point is marked on it.

From this point there are loops, i.e. closed curves that start at the base point, run on the torus surface and end again at the base point. Some of the loops can be drawn together to a point on the torus, others cannot. Imagine that the loops are made of rubber and can be stretched, compressed and shifted as desired, but always in such a way that the beginning and end remain fixed at the base point and the loops must always remain on the torus (i.e. only on the surface and not run through the "batter" of the donut). Such a deformation is called homotopy ; it is also said that a loop is homotoped . Two loops that can be transformed into one another by a homotopy are called homotop .

All loops that are homotopic to each other are grouped into a homotopy class . The different classes of homotopy form the elements of the fundamental group .

The two loops and in the figure on the right belong, for example, to different homotopy classes: They cannot be deformed into one another and therefore describe different elements of the fundamental group. Further elements are obtained by running through one of the two loops several times before closing the loop: a loop that goes around the hole twice cannot be deformed into one that goes around it three times, etc. ${\displaystyle a}$ ${\displaystyle b}$

In general, two loops can be combined into a third by going through first one, then the other, i.e. connecting the end of the first with the beginning of the second (since the connection point is now an inner point of the loop, it no longer has to be remain on the base point, but may also be pushed away from it). With this connection, the set of homotopy classes becomes a group , the so-called fundamental group. The neutral element is the class of loops that can be contracted to the base point. The inverse element of a class of loops is obtained by traversing them backwards.

Mathematical definition

Let be a topological space and a base point in . A loop is a continuous map that connects to itself, i.e. H. . ${\displaystyle X}$ ${\displaystyle p\in X}$ ${\displaystyle X}$ ${\displaystyle \gamma :[0,1]\to X}$ ${\displaystyle p}$ ${\displaystyle \gamma (0)=\gamma (1)=p}$

A homotopies between two loops and is a continuous family of loops, both loops connecting , d. h .: is a continuous mapping with the properties ${\displaystyle H}$ ${\displaystyle \gamma _{0}}$ ${\displaystyle \gamma _{1}}$ ${\displaystyle H:[0,1]\times [0,1]\to X}$

• ${\displaystyle H(0,\cdot )=\gamma _{0}}$and . ${\displaystyle H(1,\cdot )=\gamma _{1}}$
• ${\displaystyle H(\cdot ,0)=H(\cdot ,1)\equiv p}$

The first parameter of describes the progress of the loop deformation ( corresponds to and corresponds to ). The second parameter corresponds to the original loop parameter . ${\displaystyle s}$ ${\displaystyle H(s,t)}$ ${\displaystyle s=0}$ ${\displaystyle \gamma _{0}}$ ${\displaystyle s=1}$ ${\displaystyle \gamma _{1}}$ ${\displaystyle t}$

Two loops are called homotop if there is a homotopy between them. The homotopy between loops defines an equivalence relation and the equivalence classes are called homotopy classes . The set of homotopy classes forms the fundamental group of with the base point . ${\displaystyle H}$ ${\displaystyle \pi _{1}(X,p)}$ ${\displaystyle X}$ ${\displaystyle p}$

The group structure is obtained through the link given above, i.e. by connecting loops:

${\displaystyle [\gamma _{0}]+[\gamma _{1}]:=[\gamma _{0}\oplus \gamma _{1}]}$

With

${\displaystyle (\gamma _{0}\oplus \gamma _{1})(t)={\begin{cases}\gamma _{0}(2\cdot t)\,&{\text{, für }}0\leq t\leq {\frac {1}{2}}\\\gamma _{1}(2\cdot t-1)\,&{\text{, für }}{\frac {1}{2}}\leq t\leq 1\\\end{cases}}}$.

Since one can also construct a homotopy between the linked loops from homotopy between different representatives, the resulting homotopy class is independent of the choice of the respective representatives.

The neutral element of the fundamental group is the homotopy class of the constant loop and the inverse element of the homotopy class is the homotopy class of the loop that goes through the loop backwards. Closed curves, which belong to the homotopy class of the constant mapping, i.e. represent the neutral element of the fundamental group, are also referred to as contractible or null homotopic curves. ${\displaystyle \pi _{1}(X,p)}$ ${\displaystyle [\epsilon ]}$ ${\displaystyle \epsilon (t)=p}$ ${\displaystyle [\gamma ]}$ ${\displaystyle [{\bar {\gamma }}]}$ ${\displaystyle {\bar {\gamma }}(t)=\gamma (1-t)}$ ${\displaystyle \gamma }$

Independence from the base point

Since all loops start at the base point , the fundamental group only measures properties of the path-related component of . So it makes sense to assume that it is path-related . Then the choice of the base point for the fundamental group is not essential either. Rather, there is a group isomorphism if and through a curve ${\displaystyle p}$ ${\displaystyle \pi _{1}(X,p)}$ ${\displaystyle p}$ ${\displaystyle X}$ ${\displaystyle \phi \colon \pi _{1}(X,p)\to \pi _{1}(X,q)}$ ${\displaystyle p}$ ${\displaystyle q}$

${\displaystyle c\colon [0,1]\to X\qquad {\text{mit }}c(0)=p{\text{ und }}c(1)=q}$

are connected. This group isomorphism is defined by

${\displaystyle \phi ([\gamma ])=[({\bar {c}}\oplus \gamma )\oplus c]}$.

While the loops and differ, they are still homotopic and the group isomorphism can be defined across both loops. ${\displaystyle ({\bar {c}}\oplus \gamma )\oplus c}$ ${\displaystyle {\bar {c}}\oplus (\gamma \oplus c)}$

So if it is path-connected, one speaks generally of and leaves out the base point. If, on the other hand, it is not path-connected, the fundamental group may well depend on the selected base point . According to the above argument, the fundamental group is then only dependent on the path connection component of . ${\displaystyle X}$ ${\displaystyle \pi _{1}(X)}$ ${\displaystyle X}$ ${\displaystyle p\in X}$ ${\displaystyle \pi _{1}(X,p)}$ ${\displaystyle p}$

Examples

• On a sphere from dimension 2, each loop can be drawn together to one point. Hence the fundamental group of the sphere is trivial, (for ). ${\displaystyle \pi _{1}(S^{n})=\{0\}}$ ${\displaystyle n\geq 2}$
• The torus described above has the fundamental group : The two loops and are producers of the fundamental group. It is in this case abelian : The loop can be (one cuts the torus along to a point contract and on, one obtains a quadrilateral whose boundary curve exactly , and can be contracted in the interior of the square). Therefore , so . ${\displaystyle \pi _{1}(T^{2})=\mathbb {Z} ^{2}}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle aba^{-1}b^{-1}}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle aba^{-1}b^{-1}}$ ${\displaystyle aba^{-1}b^{-1}=1}$ ${\displaystyle ab=ba}$
• For a -dimensional torus we have . ${\displaystyle n}$ ${\displaystyle \pi _{1}(T^{n})=\mathbb {Z} ^{n}}$
• The two-dimensional plane with a hole has the fundamental group , just like the 1- sphere (a simple circle). The homotopy class of a loop is determined by the number of times the loop goes around the hole (e.g. clockwise). ${\displaystyle \mathbb {R} ^{2}\backslash \{0\}}$ ${\displaystyle \mathbb {Z} }$
• The two-dimensional plane with two holes has as a fundamental group a free group in two generators, namely the two loops that run once around one of the holes. This group is not Abelian.
• Fundamental groups do not torsion be: so are the fundamental groups of real projective plane or the group of rotations in space , isomorphic to the cyclic group of order. 2 ${\displaystyle \mathrm {SO} (3,\mathbb {R} )}$ ${\displaystyle \mathbb {Z} /2\mathbb {Z} }$
• One can show that for every group there is a so-called classifying space , the fundamental group of which is isomorphic . ${\displaystyle G}$ ${\displaystyle BG}$ ${\displaystyle G}$
• The fundamental group of a nodal complement is called a nodal group . It can be calculated using the Wirtinger algorithm.

Properties and uses

Overlays

The fundamental group plays a crucial role in the classification of overlays . For spaces that have a universal overlay, the fundamental group is isomorphic to the cover transformation group of the universal overlay. This isomorphism is one of the most important tools for calculating the fundamental group.

Seifert-van-Kampen's theorem

→ Main article : Seifert-van-Kampen's theorem

An important tool for calculating the fundamental group is also the Seifert-van-Kampen theorem, which allows space to be broken down into overlapping areas and the fundamental group to be calculated from the (simpler) fundamental groups of the areas and the overlap. ${\displaystyle X}$ ${\displaystyle X}$

Consequences from certain fundamental groups

Knowledge of the fundamental group often allows conclusions to be drawn about the topological space. For example, if a manifold has a finite fundamental group, it cannot carry a metric that has non-positive curvature everywhere . The only closed surface with a trivial fundamental group is the sphere. The Poincaré conjecture , which has now been proven, says that an analogous statement also applies to three-dimensional manifolds.

Connection with homology

In the general case the fundamental group does not need to be Abelian (as in the case of the torus). But you can "make" it Abelian by dividing out the commutator group . The group that is then obtained is isomorphic to the first homology group for path-connected spaces .

Generalizations

The fundamental group is the first homotopy group , hence the name . Since the definition uses one-dimensional loops, the fundamental group can only recognize the one-dimensional topological structure . A hole in a two-dimensional surface can be determined by grinding, but a hole in three-dimensional space (for example ) not: you can drag past it. ${\displaystyle \pi _{1}}$ ${\displaystyle \mathbb {R} ^{3}\backslash \{0\}}$

The generalization to the -th homotopy groups therefore uses spheres of dimension instead of loops . ${\displaystyle n}$ ${\displaystyle \pi _{n}}$ ${\displaystyle n}$

If so, the Hurewicz theorem (after Witold Hurewicz ) says that the first nontrivial homotopy group coincides with the first nontrivial homology group . ${\displaystyle \pi _{1}=\{0\}}$

With does not denote a group, but only the set of the path-related components of . Since one can understand a homotopy as a path in the loop space , becomes about ${\displaystyle \pi _{0}}$ ${\displaystyle X}$ ${\displaystyle \Omega (X,p)}$

${\displaystyle \pi _{1}(X,p)=\pi _{0}(\Omega (X,p))}$

the connection between and established. ${\displaystyle \pi _{0}}$ ${\displaystyle \pi _{1}}$

See also

• Fundamental groupoid

literature

• Tammo tom Dieck: Topologie , de Gruyter, Berlin, 2000, ISBN 3-11-016236-9
• Allen Hatcher: Algebraic topology , CUP, Cambridge, 2003, ISBN 0-521-79160-X (also Algebraic Topology )

Individual evidence

1. ↑ John. Stillwell: Mathematics and its history . Springer, New York 2010, ISBN 978-1-4419-6052-8 , pp. 485 .