curvature
Curvature is a mathematical term that, in its simplest meaning, describes the local deviation of a curve from a straight line . The same term also stands for the degree of curvature , which indicates quantitatively how strong this local deviation is for each point on the curve .
Building on the curvature term for curves, the curvature of a surface in three-dimensional space can be described by examining the curvature of curves in this surface. A certain part of the curvature information of a surface, the Gaussian curvature , depends only on the internal geometry of the surface, i. H. from the first fundamental form (or the metric tensor ), which defines how the arc length of curves is calculated.
This intrinsic curvature concept can be generalized to manifolds of any dimension with a metric tensor. The parallel transport along curves is explained on such manifolds , and the curvature quantities indicate how large the change in direction of vectors is after one revolution during parallel transport along closed curves. One application is general relativity , which describes gravity as a curvature of space-time . This term can be applied even more generally to main fiber bundles with context . These are used in gauge theory , in which the curvature quantities describe the strength of the fundamental interactions (e.g. the electromagnetic field ).
Curvature of a curve
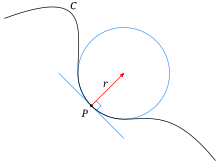
In geometry, the curvature of a flat curve is the change in direction when moving through the curve. The curvature of a straight line is zero everywhere because its direction does not change. A circle (arc) with the radius has the same curvature everywhere, because its direction changes equally strongly everywhere. The smaller the radius of the circle, the greater its curvature. The measure of the curvature of a circle is the size , the ratio of central angle and length of an arc. The central angle is equal to the outer angle between the circular tangents at the end points of the circular arc. In order to define the curvature of an arbitrary curve at a point, one considers a curve segment of the length that contains the point in question and whose tangents at the end points intersect at an angle . So that the curvature in the point is through
defined if this differential quotient exists. If the curvature at a point is not equal to zero, then the reciprocal of the curvature is called the radius of curvature ; this is the radius of the circle of curvature through this point, i.e. the circle that best approximates the curve at this point. The center of this circle is called the center of curvature and can be constructed by plotting the radius of curvature perpendicular to the tangent of the curve in the direction in which the curve bends.
If the curve is given as a graph of a function , then the following applies to the slope angle of the curve , i.e. with the chain rule . For the arc length applies or . This gives for the curvature
Here, the curvature can be positive or negative, depending on whether the angle of rise of the curve is increasing or decreasing with increasing abscissa , i.e. H. whether the function is convex or concave .
Definitions
be the position vector of a point on the curve as a function of the arc length . The curvature of the curve is then defined as
The curvature is therefore given by the amount of the derivative of the unit tangent vector according to the arc length and thus indicates how quickly the tangent direction changes depending on the arc length when passing through the curve. The curvature at one point of the curve is independent of the selected parameterization according to the arc length.
For plane curves, the curvature can be defined with a sign with respect to an orientation of the normal bundle of the curve. Such an orientation is given by a continuous unit normal vector field along the curve. It always exists because every flat curve can be oriented. If the curvature is not zero, then the curvature is signed by the scalar product
Are defined. So the curvature is positive if it curves in the direction of (i.e., if is equal to the principal normal unit vector with ) and negative if it curves in the opposite direction (i.e., if holds). The definition is again independent of the parameterization according to the arc length, but the sign depends on the choice of along the curve. The amount provides the unsigned definition of the curvature given above.
An orientation can be assigned to a regularly parameterized curve in the plane via the direction of travel. If an orientation of the plane is also specified, this induces an orientation on the normal bundle. For this purpose, let the unit normal vector be, so that the ordered basis is positively oriented. This means that the sign of the curvature of a parameterized curve is dependent on the orientation of the plane and the direction of passage of the parameterized curve. In a left turn is positive and in a right turn is negative.
A curve , which is given as a set of zeros of a function with a regular value , can be assigned the curvature with a sign with respect to the normalized gradient field restricted to the curve .
properties
The circle of curvature is the uniquely determined circle whose order of contact with the curve is at the point of contact . The curvature in a point is exactly zero if there is the contact order with the tangent . The evolution of a curve is the locus of its centers of curvature. A center of curvature is obtained as the limit value of the points of intersection of two normals which approach each other. According to Cauchy, this can be used to define the curvature of a plane curve.
The curvature of a space curve, like the winding, is a movement-invariant quantity that describes the local course of a curve. Both quantities appear as coefficients in the Frenet formulas .
If the curvature is signed for a curve parameterized according to the arc length in the oriented plane, then the following equations apply:
Either of the two equations is equivalent to defining signed curvature for parameterized curves. In Cartesian coordinates, the equations that and mean a fundamental system of solutions to the linear ordinary differential equation
form their solution by
With
given is. From the figure, in turn, the parameterization of the curve according to the arc length is obtained by integration . The specification of a starting point , a starting direction and the curvature as a function of the arc length clearly determines the curve. Since the angle is given by a rotation of , it also follows that two curves with the same curvature function only differ by an actual movement in the plane. It also follows from these considerations that the curvature is signed by
is given, where the angle of the tangent vector is to a fixed direction and is measured increasing in the positive direction of rotation.
If you restrict the parameterization of a plane curve in the vicinity of a curve point so that it is injective , then you can clearly assign the normal vector to each curve point . This assignment can be understood as mapping the curve into the unit circle by attaching the normal vector to the origin of the coordinate system. A curve segment on the unit circle of the length then belongs to a curve segment of the length that contains the point . The following then applies to the curvature at the point
This idea can be transferred to surfaces in space by taking a unit normal vector field on the surface as a mapping into the unit sphere . This mapping is called a Gaussian map . If one looks at the ratio of areas instead of the arc lengths and gives the area in the unit sphere a sign, depending on whether the Gaussian map preserves or reverses the direction of the boundary curve , then this provides the original definition of Gaussian curvature by Gauss . However, the Gaussian curvature is a quantity of the intrinsic geometry, while a curve has no intrinsic curvature, because every parameterization according to the arc length is a local isometry between a subset of the real numbers and the curve.
If one considers a normal variation , , a parameterized plane curve on a parameter interval and is denoted by the arc length of the curved piece varied, then for the curvature sign with respect to :
The curvature at a point indicates how quickly the arc length of an infinitesimal curve piece changes at this point with a normal variation. Transferred to surfaces in space, this leads to the concept of mean curvature . The corresponding limit value with areas instead of curve lengths then provides twice the mean curvature.
This characterization of the curvature of a plane curve also applies if one considers, more generally, the variation due to the local flow of a vector field (i.e. ) . You get
with the Jacobi matrix and the divergence of the vector field. As an application, one obtains the following formula for the curvature with a sign with respect to the normalized gradient field along a curve, which is given as a set of zeros of a function (the second-order contribution in the direction vanishes):
where with the Hessian matrix , the trace and the identity matrix . For images , this formula delivers twice the mean curvature of surfaces as sets of zeros in space and is called the Bonnet formula. In the case of plane curves, the formula is written out and given a different form:
Here, z. B. the partial derivative of after the first argument and the adjuncts of . For mappings , the second expression provides the Gaussian curvature for surfaces as sets of zeros in space.
Calculation of the curvature for parameterized curves
The definition given above presupposes a parameterization of the curve according to the arc length. By changing the parameters, a formula for any regular parameterizations is obtained . If you summarize the first two derivatives of as columns of a matrix , then the formula is
- .
For plane curves is a square matrix and the formula is simplified using the product rule for determinants to
- .
If the plane is given by the one with the standard orientation, then the formula for the curvature with a sign is obtained by omitting the absolute lines in the numerator.
Flat curves
If the parameterization is given by the component functions and , then the formula for the signed curvature in the point provides the expression
- .
(The dots denote derivatives according to .)
This provides the following special cases:
- case 1
- The curve is the graph of a function . The curvature in the point results from
- .
- Case 2
- The curve is given in polar coordinates , i.e. by an equation . In this case the formula
is obtained for the curvature at the point
- .
Space curves
For curves in three-dimensional space , the general formula can be expressed using the cross product as follows:
Curvature of a surface
The curvature of a curved regular surface can be seen in an outwardly quadratically increasing deviation of the surface from its tangential plane . An increased curvature is then noticeable as a greater deviation from the plane.
In differential geometry , at each point, one considers the radii of curvature of the intersection curves with the normal planes established in (i.e. planes intersecting the surface perpendicularly). The sign with respect to a unit normal vector field on the surface, restricted to the plane intersection curve, is assigned to the radii of curvature and curvatures. Among these radii of curvature there is a maximum ( ) and a minimum ( ). The reciprocal values and are called the main curvatures . The corresponding directions of curvature are perpendicular to one another.
The Gaussian curvature and the mean curvature of a regular surface at a point are calculated as follows:
The total curvature or total curvature of a surface is the integral of the Gaussian curvature over this surface:
Curvature in Riemannian geometry
Since Riemannian manifolds are generally not embedded in any space, a curvature quantity is needed in this sub-area of differential geometry that is independent of a surrounding space. To this end, the Riemann curvature tensor was introduced. This measures the extent to which the local geometry of the manifold deviates from the laws of Euclidean geometry. Further curvature quantities are derived from the curvature tensor. The most important curvature of Riemannian geometry is the cutting curvature. This derived quantity contains all information that is also contained in the Riemann curvature tensor. Other simpler derived quantities are the Ricci curvature and the scalar curvature .
A curvature on a Riemannian manifold can be seen, for example, when the ratio between the circumference and radius within the manifold is determined and compared to the value obtained in Euclidean space .
It is noteworthy that, for example, a metric can be defined on the surface of a torus that has no curvature. This can be deduced from the fact that a torus can be formed as a quotient space from a flat surface.
Application in the theory of relativity
In the general theory of relativity , gravity is described by a curvature of space-time , which is caused by the masses of the heavenly bodies. Bodies and rays of light move on the geodetic paths determined by this curvature . These paths give the impression that a force is being exerted on the corresponding body.
literature
- Wolfgang Walter: Analysis II . 2nd Edition. Springer, 1991, ISBN 3-540-54566-2 , pp. 171-174.
- Konrad Köngisberger: Analysis 1 . 2nd Edition. Springer, 1992, ISBN 3-540-55116-6 , pp. 238-41, 257.
- Ilja Nikolajewitsch Bronstein, Konstantin Adolfowitsch Semendjajew, Gerhard Musiol, Heiner Mühlig: Pocket book of mathematics . 7th edition. Verlag Harri Deutsch, 2008, ISBN 978-3-8171-2007-9 , pp. 251 ff. ( Excerpt from the English edition (Google))
- Matthias Richter: Basic knowledge of mathematics for engineers . 2nd Edition. Vieweg + Teubner 2001, 2008, ISBN 978-3-8348-0729-8 , p. 230 ( excerpt (Google))
- A. Albert Klaf: Calculus Refresher. Dover 1956, ISBN 978-0-486-20370-6 , pp. 151-168 ( excerpt (Google))
- James Casey: Exploring Curvature . Vieweg + Teubner, 1996, ISBN 978-3-528-06475-4 .
Web links
- Create animated illustrations yourself: accompanying bipod and curvature function ( Maple -Worksheet)
- Eric W. Weisstein : Curvature . In: MathWorld (English).
- Curvature in the Encyclopaedia of Mathematics
- The History of Curvature ( Memento from April 30, 2013 in the Internet Archive )
- Curvature, Intrinsic and Extrinsic on MathPages.com (English)
































































































![\ kappa (\ varphi) = {\ frac {(f (\ varphi)) ^ {2} +2 (f '(\ varphi)) ^ {2} -f (\ varphi) f' '(\ varphi)} {\ left [(f (\ varphi)) ^ {2} + (f '(\ varphi)) ^ {2} \ right] ^ {3/2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/63f440dd8ea454e44d360d19e5cfd7431b95fae9)











