Parametric representation
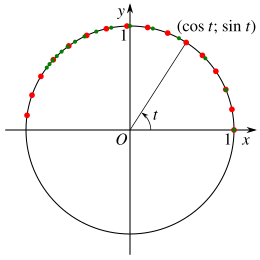
red: green: The parameters and each run from 0 to 3 with a step size of 0.2. The parameter of the first representation is the arc length. The second representation consists solely of rational functions . Both representations satisfy the circular equation
In mathematics, a parameter representation (also parameterization or parameterization ) is understood to be a representation in which the points of a curve or surface are traversed as a function of one or more variables , the parameters . One parameter is required to describe a curve in a plane or in space , and a set of two parameters to describe an area.
One example is the description of the unit circle around the origin of a Cartesian coordinate system in the plane. One possible parameter is the angle at the origin of the coordinates (see adjacent picture), which gives the following parameter representation of the position vector as a function of :
The description of the path coordinates of a moving object as a function of time is an example of a parametric representation in physics .
If a parametric representation of a curve or surface is known, the corresponding point of the curve or surface can be specified directly for each parameter (set). In contrast, it is usually more difficult to decide whether a given point lies on the curve or on the surface.
Curves or surfaces can be parameterized in different ways. In the case of curves, it is often advantageous to choose the arc length , measured from a fixed point along the curve, as a parameter. The parameters of surfaces or higher-dimensional structures are often chosen so that the parameter lines are orthogonal . Even with relatively simple structures, it is not always possible to find a parameter representation of the coordinates with the help of elementary functions for every parameterization , for example if the arc length is selected as a parameter in an ellipse .
Properties of the parametric representations
In addition to the parameter display, there are also other options for describing curves or surfaces. In the plane, for example, the graph of a function describes a curve; in three-dimensional space, the function can describe an area. These are special parameter representations when the function variables are understood as parameters. However, they are not suitable for displaying figures such as circles or spheres, as they can only assign one point to each point of the -axis or the - -plane. With the function
only a semicircle can be displayed. To get a full circle, another semicircle must be added.
Another possibility for representation is the implicit description by means of an equation of the coordinates, for example . The unit circle can be expressed in this form by the circle equation
describe. This shape is good for checking whether a given point is on a curve or plane, since it only needs to be checked that the coordinates satisfy the equation. With a such implicit equation can only objects are described whose dimension is smaller by 1 than that of the space in which they are described. An equation is enough in three-dimensional space to describe a surface, but not to describe curves.
With a parametric representation, it is easy to calculate individual points that belong to the parametrized curve or surface. It is therefore well suited for drawing these objects, for example in CAD systems. In addition, the calculated coordinates can easily be transformed into other coordinate systems so that objects can be moved, rotated or scaled relatively easily.
In physics, the parametric representation is suitable for describing the path of moving objects, with time being usually chosen as the parameter. The derivative of the position vector with respect to time then gives the time-dependent speed , the second derivative the acceleration . Conversely, if there is an initial position and initial speed at the point in time as well as an acceleration field (possibly location and time dependent) , the parameter representation of the trajectory is obtained by integration . With a constant acceleration, as with an inclined throw without air resistance, the following trajectory results, for example:
Parametric representations are also used in differential geometry . With the help of derivatives of the position vectors according to the parameters, lengths , tangent vectors or tangent planes , curvatures , angles or areas can be determined. To calculate lengths, angles and areas in areas, it is not necessary to know an explicit parameter representation of the area in space. It is sufficient if the metric ( first fundamental form ) of the area that describes the lengths along the parameter lines and the angles between the parameter lines is known. This can be advantageous for curved surfaces .
Parametric representations of lines and planes
The parametric representation (or parametric form) of a straight line equation is the form
and a plane equation the form
- ,
where and are the real parameters. The vector is the position vector of a point on the straight line or plane. This point is called the starting point or support point , and its position vector is then called the support vector . The vector in the straight line equation is called the direction vector of the straight line, the vectors and in the plane equation also direction vectors or span vectors . These vectors must not be zero vectors , and the span vectors of a plane must not be collinear . If there is a unit vector in the straight line equation , the parameter corresponds to the distance of a straight line point from .
The direction vectors of a plane equation span an affine coordinate system (indicated in the adjacent picture by the blue coordinate network within the plane), where and represent the affine coordinates. The position vector of a point on the plane is obtained by adding the -fold of the vector and then the -fold of the vector to the position vector of the point .
Regular parametric representations
A differentiable parametric representation of a curve is called regular if its derivative does not vanish at any point; it does not necessarily have to be injective . In general, a differentiable parametric representation is called regular if it is an immersion , that is, if its derivative is injective everywhere (that is, its rank is greater than or equal to the dimension of the archetype).
Generalization to a higher dimension
The generalization is obvious: Let it be a “map” of a -dimensional differentiable manifold . The map is given by a -dimensional differentiable parameterization: For points in the following applies: with differentiable functions .
For an arbitrary function of the points of the manifold the following then applies to the derivative in the direction of the tangential vector of a curve that has the curve parameter λ on the map :
Because of the chain rule, this result is independent of the selected parameterization.
Parameterization of NURBS objects
In computer graphics , parameterization is often understood to mean the distribution of curves that span a NURBS surface or of points that span a curve. The surface lines are called isoparms (isoparametric curves), the points on NURBS curves are called control vertices (CV). The representation of this structure corresponds to the parameter representation and is called component representation in the industry .
In the visualization on the right, two identically structured curves can be seen that do not have a homogeneous parameterization, e.g. a high point density at the bottom left. The blue cube does not respect the CV distribution while it is cornering. Instead, it moves at a constant speed and thus assumes a homogeneous parameterization. The green cube on the right, on the other hand, respects the different point density and always slows down where the CVs are close to one another. Both animations have the same length of 200 frames.








































