Non-Uniform Rational B-Spline

Three-dimensional NURBS surfaces can have complex, organic shapes. Control points affect the directions of the surface. The outermost square below outlines the X / Y dimensions of the surface.

NURBS area (green) of degree 4, defined by 36 control points (red) over a two-dimensional parameter area (lower grid).

Non-uniform rational B-splines (German: non-uniform rational B-splines , or NURBS for short) are mathematically defined curves or surfaces that are used in computer graphics , for example in CGI or CAD , to model any shape. A NURBS can represent any non-branching continuous line. In the computer graphics area, however, the geometry information is mostlydisplayedusing piece-wise functionally defined geometry elements, instead of depicting the entire shape using a single NURBS.

development

In the 1950s , especially in the automotive and shipbuilding industries, mathematically exact descriptions of free-form surfaces were required for error-free reproducibility of technical components . Before that time, such surfaces were described by individual physical models produced by a designer .

Among other things, the engineer Pierre Étienne Bézier , at that time at Renault in France , began developing the Bézier curve named after him . Independently of Bézier, Paul de Casteljau , employed by Citroën , was also working on this mathematical problem at the same time. Because Bézier published the results of his work, splines whose control points do not lie on the curve itself are now referred to as "Bézier splines" in graphic data processing , while de Casteljau's name lives on in the algorithm named after him that was used for the numerical processing of parametric surfaces is used. In the 1960s it became clear that non-uniform rational B-splines ( NURBS ) are a generalization of Bézier splines that can be viewed as uniform non-rational B-splines .

Initially, NURBS were only used in proprietary CAD tools from automotive companies. They later found their way into more widespread computer graphics applications, such as the Open Graphics Library (OpenGL) .

Real-time processing and interactive rendering of NURBS curves and surfaces became possible for the first time on systems from Silicon Graphics in 1989 . At CeBIT 1994, the companies CAS Berlin and CAA, in cooperation with the TU Berlin, presented the first interactive NURBS modeler for PCs, baptized under the name NöRBS. Today, most professional computer graphics applications contain NURBS technology, which in most cases is implemented by integrating a NURBS engine provided by a specialist company.

application

NURBS are almost irreplaceable in computer-aided design (CAD) and manufacturing ( CAM ) and are part of numerous industry standards such as IGES ( Initial Graphics Exchange Specification ), STEP ( STandard for the Exchange of Product model data ) and PHIGS ( Programmer's Hierarchical Interactive Graphics System ) . In general, the interactive manipulation of NURBS curves and surfaces is very intuitive and predictable. Control points are always either connected directly to the curve or surface, or appear to be connected to a rubber band. A manipulation of the geometric elements can - most obviously in the case of Bézier curves - be carried out directly at the control points or implemented using higher-level tools. Such tools are based in part on the property of NURBS to be able to display curves and surfaces of different continuity .

Here, different strengths of continuity requirements are made. In addition to the usual continuity, the geometric continuity is also considered here: ${\ displaystyle {\ mathcal {C}}}$

${\ displaystyle {\ mathcal {G}} ^ {0}:}$ Positional continuity applies when the end points of two curves or surfaces meet. Nevertheless, curves or surfaces can touch at an angle that leads to a sharp edge or corner at this point and disturbs the lighting effects.
${\ displaystyle {\ mathcal {G}} ^ {1}:}$ With tangential continuity , the parallelism of the end vectors of curves or surfaces prevents the appearance of sharp edges. Tangential continuity is often sufficient, since the illumination of such geometries appears continuous and therefore natural.
${\ displaystyle {\ mathcal {G}} ^ {2}:}$ With the same curvature values , curvature continuity prevails at the common point of adjacent curves or common lines of adjacent surfaces. This continuity is necessary, for example, for surfaces overflown in order to be able to rule out a separation of the flow.

Higher degrees of continuity are also possible with NURBS.

The realization of smooth surfaces requires NURBS surfaces that at least achieve -continuity. Defects in the surface can be detected by lighting and reflection . One method for evaluating a surface is based on the evaluation of an image recorded by ray tracing or reflection and imaging of a surface with white stripes reflected on it, with which even the smallest deviations of the surface can be revealed. This method comes from prototype construction in the automotive sector, where the surface quality is ensured by checking the reflections from a neon light on the body . ${\ displaystyle {\ mathcal {G}} ^ {1}}$

Mathematical description

NURBS curves and surfaces have a number of interesting properties:

They are invariant for projective transformations.
They provide a common mathematical representation for both analytical standard shapes (e.g. conic sections) and freeform surfaces.
They reduce the memory overhead for geometric objects (compared to simpler methods).
They can be evaluated relatively quickly using numerically stable and precise algorithms.
They are generalizations of non-rational B-splines and non-rational and rational Bézier curves and surfaces. The statement that NURBS curves are a generalization of Bézier curves means that all Bézier curves are NURBS curves, but not all NURBS curves are Bézier curves.

A NURBS curve is defined by the degree of its base polynomials (= order p of the NURBS curve - 1), a set of weighted ( ) control points and a node vector . NURBS curves and surfaces are generalizations of both B-splines and Bézier curves and surfaces. The main difference to these two types of splins is the weighting of the control points with the weights . This makes NURBS curves rational. ${\ displaystyle \ textstyle C (u)}$ ${\ displaystyle \ textstyle k}$ ${\ displaystyle \ textstyle \ mathbb {P}}$ ${\ displaystyle \ textstyle w_ {i}}$ ${\ displaystyle \ textstyle P_ {i}}$ ${\ displaystyle \ textstyle U}$ ${\ displaystyle \ textstyle w_ {i}}$ ${\ displaystyle \ textstyle w_ {i}}$

A NURBS curve is based on the sum of the control points weighted with rational B-spline basis functions , i.e. via the formula ${\ displaystyle \ textstyle R_ {i, k}}$ ${\ displaystyle \ textstyle P_ {i}}$

{\ displaystyle C (u) = \ sum _ {i = 0} ^ {n} R_ {i, k} (u) P_ {i}}

fully defined. The rational B-spline basis function is calculated from B-spline basis functions ${\ displaystyle \ textstyle N_ {i, k}}$ of the degree of basis polynomials and related to the control points weights to ${\ displaystyle \ textstyle k}$ ${\ displaystyle \ textstyle w_ {i}}$

{\ displaystyle R_ {i, k} (u) = {\ frac {N_ {i, k} (u) w_ {i}} {\ sum _ {j = 0} ^ {n} N_ {j, k} (u) w_ {j}}}}

.

The parameter switches in the area of the node vector ${\ displaystyle \ textstyle u \ in [a, b]}$

{\ displaystyle \ displaystyle U = \ {\ underbrace {a _ {(0)}, \ ldots, a _ {(p-1)}} _ {p}, u_ {p}, \ ldots, u_ {n}, \ underbrace {b _ {(n + 1)}, \ ldots, b _ {(n + p)}} _ {p} \}}

the individual segments of the spline curve are active. The elements of the knot vector are monotonically increasing, with all as well as all . ${\ displaystyle \ textstyle a _ {(i)} = a _ {(j)}}$ ${\ displaystyle \ textstyle b _ {(i)} = b _ {(j)}}$

Boundary conditions and definitions

Checkpoints

{\ displaystyle \ mathbb {P} = \ {P_ {i} \ mid P_ {i} = (x, y) {\ text {with}} x, y \ in \ mathbb {R} {\ text {and} } i = 0..n \ in \ mathbb {N} \}}

{\ displaystyle \ mid \ mathbb {P} \ mid = m = (n + 1)}

{\ displaystyle \ mathbb {W} = \ {w_ {i} \ in \ mathbb {R}, i = 0..n \ in \ mathbb {N} \}}

{\ displaystyle \ mid \ mathbb {W} \ mid = m = (n + 1)}

Knot vector

The knot vector consists of parameter values that determine the influence of the control points on the NURBS curve. The number of nodes is always equal to the number of control points plus the degree of the curve plus one ( ). For example, a third degree curve with four control points has eight nodes (4 + 3 + 1 = 8). To the graphic designer, nodes are usually not helpful; they are only required for internal calculations. For this reason, nodes in many graphic design programs cannot be changed or are visible at all. Newer versions of NURBS software (e.g. Alias Maya) allow interactive changes to node positions, which is, however, significantly less intuitive than changes to control points. ${\ displaystyle \ textstyle U}$ ${\ displaystyle \ textstyle u_ {i}}$ ${\ displaystyle \ textstyle P_ {i}}$ ${\ displaystyle \ textstyle \ mid U \ mid = r = m + k + 1 = n + p + 1}$

The values of the node vector must be in ascending order. So (0, 0, 1, 2, 3) is valid, but (0, 0, 2, 1, 3) is not. The individual knot values have no statement for themselves; only the ratios of the differences between the node values have any meaning. As a result, the node vectors (0, 0, 1, 2, 3), (0, 0, 2, 4, 6), and (1, 1, 2, 3, 4) all give the same curve. Furthermore, the multiplicity of a node must be less than or equal to the degree of the curve (no node may appear more than the degree of the curve). For first degree NURBS, each node is paired with a control point.

Order of a NURBS curve

A NURBS curve is of order , it consists of polynomials of degree . The order of a NURBS curve is determined by the number of neighboring control points that influence the curve. The curve is mathematically composed of polynomials whose degree is one less than the order of the curve ( ). So, second-order curves (which are represented by linear polynomials) are called linear curves, third-order curves are called square curves, and fourth-order curves are called cubic curves. The number of control points must be greater than or equal to the order of the curve. ${\ displaystyle \ textstyle p = k + 1}$ ${\ displaystyle \ textstyle k}$ ${\ displaystyle \ textstyle p}$ ${\ displaystyle \ textstyle k}$ ${\ displaystyle \ textstyle k = p-1}$ ${\ displaystyle \ textstyle m}$ ${\ displaystyle \ textstyle p}$

In practice, cubic curves are most often used. Fifth or sixth degree curves are sometimes useful, especially for derivations, but higher degree curves are never used in practice because they lead to internal numerical problems and their calculation tends to require a disproportionate amount of calculation time.

Unit circle

In contrast to non-rational curves, which are not suitable for representing circles, this works with NURBS without any problems. The unit circle in the xy plane can be constructed, for example, as a NURBS curve of degree 2 with a node vector (0,0,0,1,1,2,2,3,3,4,4,4) and the following control points and weights .

x	y	Weight
1	0	1
1	1	√2 / 2
0	1	1
−1	1	√2 / 2
−1	0	1
−1	−1	√2 / 2
0	−1	1
1	−1	√2 / 2
1	0	1

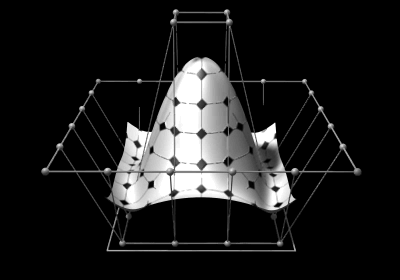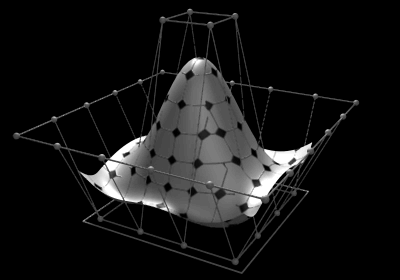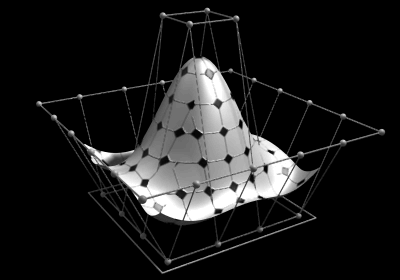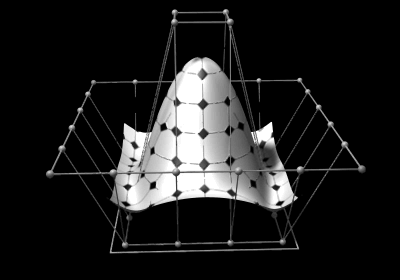
NURBS surfaces

While a NURBS curve is only spanned in one parametric direction , a NURBS surface is spanned by two parameters, named and . The curve can be mapped by evaluating different parameters in Cartesian two- or three-dimensional space. Similarly, a NURBS surface is mapped in Cartesian space by evaluating it with different values for two parameters. ${\ displaystyle u}$ ${\ displaystyle u}$ ${\ displaystyle v}$

{\ displaystyle S (u, v) = \ sum _ {i = 0} ^ {n} \ sum _ {j = 0} ^ {m} R_ {i, j} (u, v) P_ {i, j }}

are defined by a control grid and the rational basic function ${\ displaystyle P_ {i, j}}$

{\ displaystyle R_ {i, j} (u, v) = {\ frac {N_ {i, p} (u) N_ {j, q} (v) w_ {i, j}} {\ sum _ {k = 0} ^ {n} \ sum _ {l = 0} ^ {m} N_ {k, p} (u) N_ {l, q} (v) w_ {k, l}}}}

with a two-dimensional weight matrix . The second dimension of the area with the parameter is switched by the node vector constructed analogously to ${\ displaystyle w_ {i, j}}$ ${\ displaystyle S (u, v)}$ ${\ displaystyle v}$ ${\ displaystyle U}$

{\ displaystyle V = \ {\ underbrace {c, \ ldots, c} _ {q}, v_ {q + 1}, \ ldots, v_ {sq-1}, \ underbrace {d, \ ldots, d} _ {q} \}}

with order and length . ${\ displaystyle q}$ ${\ displaystyle s}$

Simple explanation of a complex issue

In the 1950s, Bézier discovered the mathematical formula with which a curved curve can be described. The curve is defined by a few so-called control points. As a result, it turned out that these Bézier curves are not yet sufficient to represent a circle exactly, for example. Then mathematical formulas were developed in which the individual control points can act differently (rationally) on the curve, the so-called B-splines. The term spline is historical and comes from shipbuilding. Ruler-like flexible metal strip, so-called traditional splines (engl. Splines) were weighed laterally with weights and could thus constitute a defined curve. Several of these curves in a row represented the frames, which in turn made the hull of the ship.

Later mathematical formulas were developed that generalized both Bézier's formula and the B-splines, the so-called "Non uniform rational B-splines". So you can display any curves and if you add not only one direction ("length") as with a curve, but a second one ("width"), any surfaces can be displayed. Theoretically, these surfaces can be as complex and large as desired. However, since the effort to calculate the formulas increases sharply with increasing complexity and can no longer be calculated in a reasonable time even with a powerful computer, more complicated areas are represented by several so-called patches. In the meantime, NURBS are used almost exclusively in industrial production in order to be able to depict every type of object to be manufactured (yoghurt cups, motor housings, sunglasses, etc.) mathematically exactly.

literature

Les Piegl, Wayne Tiller: The NURBS Book. Monographs in Visual Communication. Springer, 2000.
David F. Rogers: An Introduction to NURBS With Historical Perspective. Academic Press, 2001.
Lyle Ramshaw: Blossoming: A connect-the-dots approach to splines. Research Report 19, Compaq Systems Research Center, Palo Alto CA June 1987.
James D. Foley, Andries van Dam, Steven K. Feiner, John F. Hughes: Computer Graphics - Principles and Practice. 2nd ed. Addison-Wesley, 1996.
David Salomon: Curves and Surfaces for Computer Graphics. Springer Science + Business Media, 2006, ISBN 0-387-24196-5 .

Web links

TinySpline - Open Source C program library with bindings for different languages