Plane equation

Plane equations and their relationships

In mathematics, a plane equation is an equation that describes a plane in three-dimensional space. A plane consists of those points in a Cartesian coordinate system whose coordinate vectors satisfy the plane equation.

If the individual coordinates of the plane points are in an equation relationship, one speaks of a coordinate equation, to which the coordinate form and the axis intercept form belong. If the position vectors of the plane points are in the equation, it is a vector equation to which the parametric form and the three-point form belong. If the equation contains a normal vector of the plane, one speaks of a normal equation, which includes the normal form and the Hessian normal form .

Vector equations can also be used to represent planes in higher-dimensional spaces, while coordinate equations and normal equations describe hyperplanes in this case .

Coordinate equations

In analytical geometry , every point in three-dimensional space is identified by a coordinate tuple with the aid of a Cartesian coordinate system . An equation with the unknowns , and then describes a set of points in space, namely those points whose coordinates satisfy the equation. Levels are distinguished by the fact that such an equation is a linear equation . Different spellings are used for the notation of levels. The spelling most commonly used in school mathematics ${\ displaystyle (x, y, z)}$ ${\ displaystyle x}$ ${\ displaystyle y}$ ${\ displaystyle z}$

{\ displaystyle E \ colon \, 2x + 3y = z}

means that the plane consists of those points whose coordinates satisfy the plane equation . The set notation used in higher mathematics reads accordingly ${\ displaystyle E}$ ${\ displaystyle (x, y, z)}$ ${\ displaystyle 2x + 3y = z}$

{\ displaystyle E = \ {(x, y, z) \ in \ mathbb {R} ^ {3} \ mid 2x + 3y = z \}}

.

There are now different forms of representation for plane equations, depending on which parameters are specified for the plane.

Coordinate shape

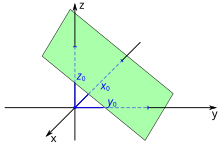
In the coordinate form a plane by four real numbers , , and described. A plane then consists of those points whose coordinates the equation ${\ displaystyle a}$ ${\ displaystyle b}$ ${\ displaystyle c}$ ${\ displaystyle d}$ ${\ displaystyle (x, y, z)}$

{\ displaystyle ax + by + cz = d}

fulfill. At least one of the three numbers must be non-zero. The coordinate form corresponds to the normal form (see below) after expansion, where , and are the components of the (not necessarily normalized) normal vector and are set, where the support vector is the plane (see below). The distance between the plane and the origin of coordinates is then given by. If the normal vector is normalized, then the distance is even . ${\ displaystyle a, b, c}$ ${\ displaystyle a}$ ${\ displaystyle b}$ ${\ displaystyle c}$ ${\ displaystyle {\ vec {n}} = (a, b, c)}$ ${\ displaystyle d = {\ vec {p}} \ cdot {\ vec {n}}}$ ${\ displaystyle {\ vec {p}}}$ ${\ displaystyle | d | / | {\ vec {n}} |}$ ${\ displaystyle | d |}$

Intercept shape

In the case of the intercept shape, a plane that is not an origin plane is described by three intercepts , and . A plane then consists of those points whose coordinates the equation ${\ displaystyle x_ {0}}$ ${\ displaystyle y_ {0}}$ ${\ displaystyle z_ {0}}$ ${\ displaystyle (x, y, z)}$

{\ displaystyle {\ frac {x} {x_ {0}}} + {\ frac {y} {y_ {0}}} + {\ frac {z} {z_ {0}}} = 1}

fulfill. Here , and are the points of intersection of the plane with the three coordinate axes , which are also referred to as track points . The lines of intersection of the plane with the three coordinate planes are called track lines and form the track triangle . If a plane runs parallel to one or two coordinate axes, the respective trace point and thus the corresponding term in the axis intercept form are omitted. The axis intercept form can be calculated from the coordinate form by dividing by . ${\ displaystyle (x_ {0}, 0,0)}$ ${\ displaystyle (0, y_ {0}, 0)}$ ${\ displaystyle (0,0, z_ {0})}$ ${\ displaystyle d}$

Vector equations

Layers are often described with the help of vectors . A plane then consists of the set of points whose position vectors satisfy the plane equation. The position vector of a point is usually called a column vector ${\ displaystyle (x_ {1}, x_ {2}, x_ {3})}$

{\ displaystyle {\ vec {x}} = {\ begin {pmatrix} x_ {1} \\ x_ {2} \\ x_ {3} \ end {pmatrix}}}

written down. Vector equations are then to be understood component-wise, that is, each component of the vector must satisfy the equation. Each point of the plane is described depending on two real parameters . In this way a parametric representation of the plane is obtained.

Parametric shape

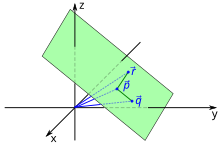
In the parameter shape or point direction form a plane by a support vector and two direction vectors and described. A plane then consists of those points in space whose position vectors give the equation ${\ displaystyle {\ vec {p}}}$ ${\ displaystyle {\ vec {u}}}$ ${\ displaystyle {\ vec {v}}}$ ${\ displaystyle {\ vec {x}}}$

{\ displaystyle {\ vec {x}} = {\ vec {p}} + s {\ vec {u}} + t {\ vec {v}}}

With

{\ displaystyle s, t \ in \ mathbb {R}}

fulfill. The support vector is the position vector of any point in the plane, which is also referred to as a support point or reference point. The two direction vectors, also called span vectors, must lie in the plane and not equal the zero vector . They must also not be collinear , i.e. they cannot be a multiple of and vice versa. The direction vectors span an affine coordinate system, the affine coordinates of a point on the plane. Exactly one point on the plane then corresponds to each value pair of these parameters. ${\ displaystyle {\ vec {u}}}$ ${\ displaystyle {\ vec {v}}}$ ${\ displaystyle (s, t)}$

Three point shape

In the three points form a plane through the local vectors , and three points of the plane described. A plane then consists of those points in space whose position vectors give the equation ${\ displaystyle {\ vec {p}}}$ ${\ displaystyle {\ vec {q}}}$ ${\ displaystyle {\ vec {r}}}$ ${\ displaystyle {\ vec {x}}}$

{\ displaystyle {\ vec {x}} = {\ vec {p}} + s ({\ vec {q}} - {\ vec {p}}) + t ({\ vec {r}} - {\ vec {p}})}

With

{\ displaystyle s, t \ in \ mathbb {R}}

fulfill. The three points must not all lie on a straight line . Here, too, exactly one point on the level corresponds to each value pair of the parameters . The point directional form is obtained from the three-point form by selecting one of the three points as the starting point and choosing the connection vectors from this point to the other two points as the direction vectors . A related representation of a plane using three plane points uses barycentric coordinates . ${\ displaystyle (s, t)}$

Normal equations

In the normal forms of a plane equation, the points of the plane are characterized by a scalar equation with the help of a normal vector of the plane. The scalar product of two vectors is used for this, which is defined by

{\ displaystyle {\ vec {x}} \ cdot {\ vec {y}} = x_ {1} y_ {1} + x_ {2} y_ {2} + x_ {3} y_ {3}}

is defined. This gives an implicit representation of the plane.

Normal form

In the normal form, a plane is described by a support vector and a normal vector . A plane then consists of those points in space whose position vectors give the equation ${\ displaystyle {\ vec {p}}}$ ${\ displaystyle {\ vec {n}}}$ ${\ displaystyle {\ vec {x}}}$

{\ displaystyle ({\ vec {x}} - {\ vec {p}}) \ cdot {\ vec {n}} = 0}

fulfill. The scalar product of two vectors (not equal to the zero vector) is equal to zero if the two vectors are perpendicular to one another. In the normal form, a plane therefore consists of those points in space for which the difference vector from the position vector and the support vector is perpendicular to the normal vector of the plane. A normal vector of the plane via the cross product can be determined from two span vectors of the plane and . ${\ displaystyle {\ vec {u}}}$ ${\ displaystyle {\ vec {v}}}$ ${\ displaystyle {\ vec {n}} = {\ vec {u}} \ times {\ vec {v}}}$

Hessian normal form

In the Hessian normal form, a plane is described by a standardized and oriented normal vector and the distance from the coordinate origin . A plane then consists of those points in space whose position vectors give the equation ${\ displaystyle {\ vec {n}} _ {0}}$ ${\ displaystyle d}$ ${\ displaystyle {\ vec {x}}}$

{\ displaystyle {\ vec {x}} \ cdot {\ vec {n}} _ {0} = d}

fulfill. The normal vector must have a length of one and point from the origin of the coordinates in the direction of the plane. The Hessian normal form is obtained from the normal form by normalizing and orienting the normal vector and then by selecting . The Hessian normal form allows an efficient calculation of the distance of any point in space to the plane, because the scalar product corresponds precisely to the length of the orthogonal projection of any vector onto the straight line through the origin with direction vector . ${\ displaystyle d = {\ vec {p}} \ cdot {\ vec {n}} _ {0}}$ ${\ displaystyle {\ vec {x}} \ cdot {\ vec {n}} _ {0}}$ ${\ displaystyle {\ vec {x}}}$ ${\ displaystyle {\ vec {n}} _ {0}}$

Generalizations

Levels can also be viewed in higher-dimensional spaces. A plane is then a linear 2-manifold in -dimensional Euclidean space . The parametric form and the three-point form retain their representation, with only -component instead of three-component vectors being used. Due to the implicit forms, however, a level is no longer described in higher-dimensional spaces, but a hyperplane of the dimension . However, each plane can be represented as an intersection of hyperplanes with linearly independent normal vectors and must therefore satisfy as many coordinate equations at the same time. ${\ displaystyle n}$ ${\ displaystyle \ mathbb {R} ^ {n}}$ ${\ displaystyle n}$ ${\ displaystyle n-1}$ ${\ displaystyle n-2}$

literature

Steffen Goebbels, Stefan Ritter: Understanding and applying mathematics . Springer, 2011, ISBN 978-3-8274-2762-5 .
Lothar Papula: Mathematical formula collection: For engineers and natural scientists . Springer, 2009, ISBN 978-3-8348-9598-1 .
Thomas Westermann: Mathematics for Engineers . Springer, 2008, ISBN 978-3-540-77731-1 .

Web links

Wikibooks: Linear Algebra: Vector Calculation: Levels - Learning and Teaching Materials

Vectors - plane equation in normal form. In: Telekolleg. Bayerischer Rundfunk, January 10, 2013, accessed on February 10, 2014 .
Eric W. Weisstein : Plane . In: MathWorld (English).
pahio: Equation of plane . In: PlanetMath . (English)