Three point shape

The three points form or three-point form is in mathematics a special form of a plane equation . In the three-point form, a plane in Euclidean space is represented using three points on the plane. The position vector of one of the three points serves as a support vector of the plane, while the difference vectors to the position vectors of the other two points form the direction vectors of the plane. Each point on the plane is then described as a function of two parameters . The three-point shape is therefore a special parametric representation of the plane.

The form of a straight line equation corresponding to the three-point form is called the two-point form.

presentation

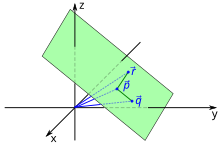
Three-point shape of a plane

In the three points form a plane in three-dimensional space by the local vectors , and three points of the plane described. A plane then consists of those points in space whose position vectors give the equation ${\displaystyle {\vec {p}}}$ ${\displaystyle {\vec {q}}}$ ${\displaystyle {\vec {r}}}$ ${\displaystyle {\vec {x}}}$

${\displaystyle {\vec {x}}={\vec {p}}+s({\vec {q}}-{\vec {p}})+t({\vec {r}}-{\vec {p}})}$   For   ${\displaystyle s,t\in \mathbb {R} }$

fulfill. The three points must not be collinear , i.e. not all lie on a straight line . This is exactly the case when the cross product is. The vector serves as a support vector for the plane, while the difference vectors and the direction vectors form the plane. ${\displaystyle ({\vec {q}}-{\vec {p}})\times ({\vec {r}}-{\vec {p}})\neq {\vec {0}}}$ ${\displaystyle {\vec {p}}}$ ${\displaystyle {\vec {q}}-{\vec {p}}}$ ${\displaystyle {\vec {r}}-{\vec {p}}}$

In the three-point form, the points of the plane are shown depending on the two parameters and . Each value pair of these parameters corresponds exactly to one point on the level. The two direction vectors spanning an affine coordinate system, the affine coordinates of a point on the plane. ${\displaystyle s}$ ${\displaystyle t}$ ${\displaystyle (s,t)}$

example

Written out is the three-point form of a plane equation

${\displaystyle {\begin{pmatrix}x_{1}\\x_{2}\\x_{3}\end{pmatrix}}={\begin{pmatrix}p_{1}\\p_{2}\\p_{3}\end{pmatrix}}+s{\begin{pmatrix}q_{1}-p_{1}\\q_{2}-p_{2}\\q_{3}-p_{3}\end{pmatrix}}+t{\begin{pmatrix}r_{1}-p_{1}\\r_{2}-p_{2}\\r_{3}-p_{3}\end{pmatrix}}={\begin{pmatrix}p_{1}+s(q_{1}-p_{1})+t(r_{1}-p_{1})\\p_{2}+s(q_{2}-p_{2})+t(r_{2}-p_{2})\\p_{3}+s(q_{3}-p_{3})+t(r_{3}-p_{3})\end{pmatrix}}}$

with . For example, if the three position vectors are , and , then the plane equation is obtained ${\displaystyle s,t\in \mathbb {R} }$ ${\displaystyle {\vec {p}}=(3,2,1)^{T}}$ ${\displaystyle {\vec {q}}=(5,1,1)^{T}}$ ${\displaystyle {\vec {r}}=(2,2,3)^{T}}$

${\displaystyle {\begin{pmatrix}x_{1}\\x_{2}\\x_{3}\end{pmatrix}}={\begin{pmatrix}3\\2\\1\end{pmatrix}}+s{\begin{pmatrix}5-3\\1-2\\1-1\end{pmatrix}}+t{\begin{pmatrix}2-3\\2-2\\3-1\end{pmatrix}}={\begin{pmatrix}3+2s-t\\2-s\\1+2t\end{pmatrix}}}$.

Each choice of , for example or , then results in a plane point. ${\displaystyle (s,t)}$ ${\displaystyle (0,0)}$ ${\displaystyle (1,2)}$

calculation

From the parametric form of a plane equation with a support vector and the two direction vectors and , in addition to the support vector, two further position vectors of points on the plane can be determined simply by choosing ${\displaystyle {\vec {p}}}$ ${\displaystyle {\vec {u}}}$ ${\displaystyle {\vec {v}}}$

${\displaystyle {\vec {q}}={\vec {p}}+{\vec {u}}}$   and   ${\displaystyle {\vec {r}}={\vec {p}}+{\vec {v}}}$

Find. From the other forms of plane equations, the coordinate form , the axis intercept form , the normal form and the Hessian normal form , the associated parameter form of the plane is first determined (see calculation of the parameter form ) and then the three-point form.

Further representations

Homogeneous presentation

A related representation of a plane using three plane points uses barycentric coordinates . A level is then given by the equation

${\displaystyle {\vec {x}}=\lambda {\vec {p}}+\mu {\vec {q}}+\nu {\vec {r}}}$   for     with   ${\displaystyle \lambda ,\mu ,\nu \in \mathbb {R} }$ ${\displaystyle \lambda +\mu +\nu =1}$

described. Here are the normalized barycentric coordinates of a point on the plane. If all three coordinates are positive, the point on the plane lies within the triangle that is described by the three specified points. If one or two coordinates are negative, the point on the plane lies outside this triangle. The barycentric coordinates are special homogeneous affine coordinates, while inhomogeneous affine coordinates are used in the three-point form. The equivalence of both representations results directly from the equation ${\displaystyle (\lambda ,\mu ,\nu )}$

${\displaystyle {\vec {x}}={\vec {p}}+s({\vec {q}}-{\vec {p}})+t({\vec {r}}-{\vec {p}})=(1-s-t){\vec {p}}+s{\vec {q}}+t{\vec {r}}}$

and the observation that applies. ${\displaystyle (1-s-t)+s+t=1}$

Representation as a determinant

A plane that runs through three specified points can also be determined using the determinant of a matrix via the equation

${\displaystyle \det {\begin{pmatrix}x_{1}&p_{1}&q_{1}&r_{1}\\x_{2}&p_{2}&q_{2}&r_{2}\\x_{3}&p_{3}&q_{3}&r_{3}\\1&1&1&1\end{pmatrix}}=0}$

or equivalent to it

${\displaystyle \det {\begin{pmatrix}x_{1}-p_{1}&q_{1}-p_{1}&r_{1}-p_{1}\\x_{2}-p_{2}&q_{2}-p_{2}&r_{2}-p_{2}\\x_{3}-p_{3}&q_{3}-p_{3}&r_{3}-p_{3}\end{pmatrix}}=0}$

To be defined. Such a representation is also called the determinant form of a plane equation. From the properties of the late product it follows about

${\displaystyle ({\vec {x}}-{\vec {p}},{\vec {q}}-{\vec {p}},{\vec {r}}-{\vec {p}})=({\vec {x}}-{\vec {p}})\cdot (({\vec {q}}-{\vec {p}})\times ({\vec {r}}-{\vec {p}}))=({\vec {x}}-{\vec {p}})\cdot {\vec {n}}=0}$

the equivalence to the normal form of a plane equation.

generalization

In general, the three-point shape can be used to describe not only planes in three-dimensional space, but also in higher-dimensional spaces. In -dimensional Euclidean space, a plane accordingly consists of those points whose position vectors give the equation ${\displaystyle n}$ ${\displaystyle {\vec {x}}}$

${\displaystyle {\vec {x}}={\vec {p}}+s({\vec {q}}-{\vec {p}})+t({\vec {r}}-{\vec {p}})}$   For   ${\displaystyle s,t\in \mathbb {R} }$

fulfill. It is only calculated with -component instead of three-component vectors. The representation with barycentric coordinates is also retained in analog form in higher-dimensional spaces. ${\displaystyle n}$

literature

• Lothar Papula: Mathematics for Engineers and Natural Scientists 1 . Springer, 2007, ISBN 978-3-8348-0224-8 .
• Thomas Westermann: Mathematics for Engineers . Springer, 2008, ISBN 978-3-540-77731-1 .