Position vector
In mathematics and in physics, a position vector (also radius vector or position vector ) of a point is a vector that points from a fixed reference point to this point (location). In elementary and synthetic geometry , these vectors can be defined as classes of arrows with the same displacement or as parallel displacements .
Position vectors make it possible to use vector calculation for the description of points , sets of points and images . If a Cartesian coordinate system is used as a basis, the origin of the coordinates is generally chosen as the reference point for the position vectors of the points. In this case the coordinates of a point with respect to this coordinate system coincide with the coordinates of its position vector.
In analytical geometry , position vectors are used to describe images of an affine or Euclidean space and to describe sets of points (such as straight lines and planes ) by means of equations and parametric representations .
In physics , position vectors are used to describe the location of a body in Euclidean space. In coordinate transformations, position vectors show a different transformation behavior than covariant vectors .
Spellings
In geometry, the reference point (origin) is usually referred to as (for Latin origo ). The notation for the position vector of a point is then:
Occasionally the lowercase letters with vector arrows are also used, which correspond to the uppercase letters with which the points are designated, for example:
The notation that the capital letter denoting the point is provided with a vector arrow is also common:
In physics in particular, the position vector is also called the radius vector and is written with a vector arrow as or (especially in theoretical physics) in semi-bold as .
Examples and applications in geometry
Connection vector
For the connection vector of two points and with the position vectors and the following applies:
Cartesian coordinates
The following applies to the coordinates of the position vector of the point with the coordinates :
shift
A shift around the vector maps the point onto the point . Then the following applies to the position vectors:
Rotation around the origin
A rotation in the plane with the center of rotation to the angle counter -clockwise , with the aid of a as follows in Cartesian coordinate rotation matrix will be described: If the position vector of a point and the position vector of the pixel , then:
Affine figure
A general affine mapping that maps the point to the point can be represented with position vectors as follows:
Here, the position vector von , the position vector von , is a linear mapping and a vector that describes a displacement. In Cartesian coordinates, the linear mapping can be represented by a matrix and the following applies:
In three-dimensional space this results in:
Corresponding representations are also available for other dimensions.
Parametric representation of a straight line
The straight line through the points and contains exactly those points whose position vector is the representation
- With
owns. One speaks here of the parametric form of a straight line equation .
Normal form of the plane equation
The plane through the point (support point) with normal vector contains exactly those points whose position vector corresponds to the normal equation
Fulfills. It is the position vector ( support vector ) of the support point and the Malpunkt denotes the scalar product .
Position vector in different coordinate systems
The point described by a position vector can be expressed by the coordinates of a coordinate system, the reference point of the position vector usually being placed in the coordinate origin .
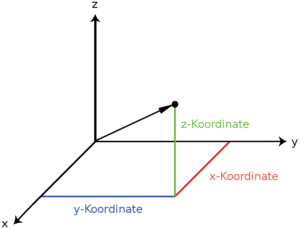
Cartesian coordinates
Usually the position vector is in Cartesian coordinates in the form
Are defined. Therefore the Cartesian coordinates are also the components of the position vector.
Cylindrical coordinates
The position vector as a function of cylinder coordinates is obtained by converting the cylinder coordinates into the corresponding Cartesian coordinates
Here denotes the distance of the point from the -axis, the angle is counted from the -axis in the direction of the -axis. and are therefore the polar coordinates of the point projected orthogonally onto the - plane.
From a mathematical point of view, the mapping (function) that assigns the Cartesian coordinates of the position vector to the cylinder coordinates is considered here .
Spherical coordinates
The position vector as a function of spherical coordinates is obtained by converting the spherical coordinates into the corresponding Cartesian coordinates
Here denotes the distance of the point from the origin (i.e. the length of the position vector), the angle is measured in the - -plane from the -axis in the direction of the -axis, the angle is the angle between the -axis and the position vector.
physics
Celestial mechanics
In order to indicate the position of a celestial body moving on an orbit around a center of gravity , this center of gravity is selected as the origin of the location or radius vector in celestial mechanics . The radius vector then always lies in the direction of the gravitational line . The path of the position vector is called the driving beam . The driving beam plays a central role in Kepler's second law (area theorem) .
See also
Individual evidence
- ↑ Istvan Szabó : Introduction to Technical Mechanics. Springer, 1999, ISBN 3-540-44248-0 , p. 12.
literature
- Klaus Desch: Mathematical Supplements to Physics II, Chapter 11: Vector Analysis. (PDF, 210 kB). Institute for Experimental Physics, Hamburg.