Kepler's laws
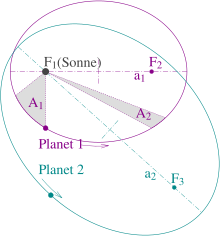
1. Two elliptical orbits with the sun at the focal point F 1 .
F 2 and a 1 are the other focal point or the major semi-axis for Planet1, F 3 and a 2 for Planet2.
2. The two gray sectors A 1 and A 2 , which have the same area, are swept over in the same time.
3. The squares of the orbital times of Planet1 and Planet2 behave like a 1 3 : a 2 3 .
The three Kepler laws are the fundamental laws of the orbit of the planets around the sun. Johannes Kepler found it at the beginning of the 17th century when he tried to adapt the heliocentric system according to Copernicus to the precise astronomical observations of Tycho Brahe . At the end of the 17th century, Isaac Newton was able to derive Kepler's laws in the classical mechanics he founded as an exact solution to the two-body problem when there is an attraction between the two bodies that decreases with the square of the distance. Kepler's laws are:
- First Kepler's Law
- The planets move on elliptical orbits. The sun is in one of its focal points.
- Second Kepler's law
- A beam drawn from the sun to the planet covers areas of the same size at the same time.
- Third Kepler's Law
- The squares of the orbital times of two planets behave like the cubes (third powers ) of the major semiaxes of their orbital ellipses .
Kepler's laws apply to the planets in the solar system to a good approximation. The deviations in the positions in the sky are usually smaller than one angular minute , i.e. approx. 1/30 full moon diameter. They are known as orbital disruptions and are mainly based on the fact that the planets are not only attracted by the sun, but also attract each other. Further, much smaller corrections can be calculated according to the general theory of relativity .
Kepler's laws represented an essential step in overcoming medieval to modern science. They are of fundamental importance in astronomy to this day .
story
Kepler's starting point
Kepler was convinced of the heliocentric system of Copernicus (1543) because it was conceptually simpler and got along with fewer assumed circles and parameters than the geocentric system of Ptolemy, which had prevailed from about AD 150. The Copernican system also made it possible to ask further questions, because for the first time the size of all planetary orbits in relation to the size of the earth's orbit was clearly defined here, without trying further hypotheses . Kepler spent his life looking for a deeper explanation for these proportions. At that time it also became clear that the planets could not be moved by fixed rotating crystal spheres in a given way along their deferents and epicycles , because, according to Tycho Brahe's observations on the comet of 1577, it should have penetrated several such shells. Apparently the planets found their way through space on their own. Their speeds, which could be determined from the size of their orbit and their orbital time, were in contradiction to the philosophically based assumptions in the Ptolemaic system. It was well known that they did not remain constant along the path, but now, like the shape of the paths, demanded a new explanation. All of this motivated Kepler to take the decisive step in astronomy, to assume "physical" causes for planetary motion, that is, those that were already revealed when studying earthly motions. In doing so, he contradicted the up to then sacrosanct Aristotelian doctrine of a fundamental opposition between heaven and earth and made a significant contribution to the Copernican turn .
In order to investigate this more precisely, it was first necessary to determine the actual orbits of the planets. For this purpose, Kepler had access to data from Tycho's decades of sky observations, which were not only much more accurate for the first time since ancient times (maximum uncertainty of approx. Two angular minutes), but also extended over large parts of the planetary orbits. When evaluating these data, Kepler for the first time consistently followed the guiding principle that the physical cause of the planetary movements lies in the sun, and consequently not in the fictitious point called the " central sun " (introduced by Ptolemy and placed in the empty center of that circle by Copernicus that he had assigned to the earth), but in the true physical sun. He imagined that the sun was acting on the planets like a magnet, and he also carried out this picture in detail.
In his work, Kepler broke new ground in other ways as well. As a starting point for the analysis of the orbits, unlike all earlier astronomers, he did not take the uniform circular motion prescribed by the philosophers since Plato and Aristotle, to which further uniform circular motions were then added in order to improve the correspondence with the planetary positions observed in the sky ( epicyclic theory ). Rather, he tried to reconstruct the actual orbits and the variable speed with which the planets run on them directly from the observations of the sky.
Thirdly, Kepler also broke new ground in the way his work was presented. Until then, it was customary for astronomers to describe their view of the world in a fully developed state. They explained how to build it up piece by piece, citing philosophical or theological justifications for each of the necessary individual assumptions. Kepler, on the other hand, described step by step the actual progress of his many years of work, including his intermittent failures due to unsuitable approaches. In 1609 he published the first part of his results as Astronomia Nova with the significant addition in the title (translated) "New astronomy, causally founded, or physics of the sky, [...] according to the observations of the nobleman Tycho Brahe". The work culminates in Kepler's first two laws, each of which applies to a single planetary orbit. Kepler's deeper explanation of the entire system and the relationships between the planetary orbits appeared in 1619 under the title Harmonices mundi ("Harmonies of the World"). There is a proposition in it that later became known as Kepler's third law.
Kepler's approach
Kepler's first result at work was that neither the Ptolemaic nor the Copernican system could reproduce the planetary positions with sufficient accuracy, even after improving individual parameters, e.g. B. the eccentricities . However, he continued to use these models as an approximation in order to select those from Tycho's observations that would be most suitable for a more precise characterization of the orbits. So he found that the eccentric orbits of Mars and Earth with respect to the fixed stars (with sufficient accuracy) remain fixed, that each runs in a plane in which the sun is, and that the two orbital planes are slightly inclined towards each other.
So Kepler could assume that Mars, although its exact orbit was still unknown, would take up the same position in space after each of its orbits around the sun, even if it appears at different heavenly positions when viewed from the earth, because then the earth each Sometimes it is at a different point in its path. From this he initially determined the earth's orbit with approx. Four-digit accuracy. On this basis, he evaluated the other observations of Mars, in which the deviations from a circular path are more pronounced than in the case of Earth. When, after many failures and long trials, he could not press the maximum error in the position of Mars in the sky below eight angular minutes (about 1/4 full moon diameter), he took another attempt and found - half by chance - that the orbit of Mars was best through a Ellipse is to be reproduced, with the sun in one of its focal points. This result was also confirmed for the earth's orbit, and it also matched all other planets observed by Tycho. Kepler knew that an elliptical path can also be composed exactly from two circular movements, but he did not consider this possibility any further. For an exact representation of the movement, these circular movements would have to run around their respective center points with variable speed, for which no physical reason is apparent:
"Kepler did not make use of the epicyclic generation of the ellipse because it does not agree with the natural causes which produce the ellipse [...]. "
In the subsequent search for the law of the entire structure of the solar system, which in turn lasted about a decade, Kepler pursued the idea of a harmony underlying the plan of creation, which - as in the case of harmony in music - should be found in simple numerical relationships . He published his result in 1619 as Harmonice mundi ('Harmonies of the World'). For later astronomy only the short message (in the 5th book of the work) is of lasting value, according to which the squares of the orbital times of all planets are in the same ratio as (in modern words) the third powers of the major semiaxes of their orbital ellipses.
Kepler also looked for a physical explanation of how the sun could act on the planets to cause the observed movements. His reflections on a magnetic action at a distance or an anima motrix inherent in the planets remained fruitless. Isaac Newton was later able to prove that Kepler's three laws represent the exact solution of the motion of a body under the action of a force according to Newton's law of gravitation . This is considered a significant step in the development of classical mechanics and modern science as a whole.
Heliocentric and fundamental formulation of the laws
Kepler formulated the law for the planets known to him. For the laws, however, the cosmological principle applies , since they are valid everywhere in the universe .
The heliocentric case of the solar system is, however, by far the most important, which is why the literature is often formulated restrictively for planets only. They are of course also valid for the moons , the asteroid belt and the Oort cloud , or the rings of Jupiter and Saturn , for star clusters as well as for objects in orbit around the center of a galaxy , and for all other objects in space . They also form the basis of space travel and the orbits of satellites .
On a cosmic scale, however, the relativistic effects are beginning to have an increasing effect, and the differences to the Kepler model serve primarily as a test criterion for more modern concepts about astrophysics. The mechanisms of formation in spiral galaxies, for example, can no longer be consistently reproduced with a model based purely on Kepler's laws.
Derivation and modern representation
Kepler tried to describe the planetary movements with his laws. From the values he observed, especially the orbit of Mars, he knew that he had to deviate from the ideal of circular orbits. Unlike Newton's later theoretical derivations, his laws are therefore empirical. From today's point of view, however, we can start from the knowledge of Newton's gravity and thus justify the validity of Kepler's laws.
Kepler's laws can be elegantly derived directly from Newton's theory of motion.
The first law follows from Clairaut's equation , which describes a complete solution of a movement in rotationally symmetrical force fields.
The second law is a geometric interpretation of the conservation of angular momentum .
By means of integration, the Kepler equation and the Gaussian constant , the third law follows from the second or, by means of the hodograph, directly from Newton's laws. In addition, according to the principle of mechanical similarity , it follows directly from the inverse-quadratic dependence of the gravitational force on the distance.
First Kepler's law (theorem of ellipses)
- The orbit of a satellite is an ellipse . One of their focal points lies in the center of gravity of the system.
This law results from Newton's law of gravitation , provided that the mass of the central body is significantly greater than that of the satellite and the effect of the satellite on the central body can be neglected.
The energy for a satellite with mass in the Newtonian gravitational field of the sun with mass is in cylindrical coordinates
With the help of angular momentum and
allows the energy equation
reshape. This differential equation is used with the polar coordinate representation
of a conic section. This is done using the derivative
and all expressions that contain are formed by substituting the to
transformed equation of the trajectory is eliminated:
by comparing the coefficients of the powers of
This solution depends only on the specific energy and the specific orbital angular momentum . The parameter and the numerical eccentricity are the design elements of the path . In the event, the following applies:
- ... first Kepler's law
| Major semi-axis | |
| Small semi-axis | |
| Foci |
|
| Pericenter | |
| Apocenter |
If (unlike Kepler) one does not take a centrally symmetrical force field as a basis, but instead reciprocally acting gravitation, then elliptical orbits are also formed. Both bodies move, however, the center of the orbits is the common center of gravity of the "central body" and Trabant, the total mass of the system is to be assumed as the fictitious central mass. However, the common center of gravity of the solar system planets and the sun (the barycenter of the solar system) is still within the sun: The sun does not rest relative to it, but rather swings a little under the influence of the orbiting planets ( length of the sun ≠ 0). The earth-moon system , on the other hand, shows greater fluctuations in terms of the orbit geometry; here, too, the system's center of gravity is still within the earth. Satellites even react to fluctuations in the force field, which is irregular due to the shape of the earth .
Although Kepler's laws were originally formulated only for the gravitational force, the above solution also applies to the Coulomb force . For charges that repel each other, the effective potential is then always positive and only hyperbolic orbits are obtained.
For forces there is another conserved quantity that is decisive for the direction of the elliptical orbit, the Runge-Lenz vector , which points along the main axis. Small changes in the force field (usually due to the influences of the other planets) let this vector slowly change its direction. B. the perihelion of Mercury's orbit can be explained.
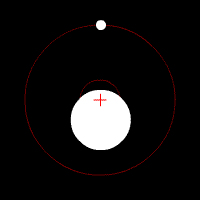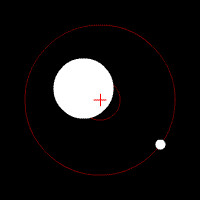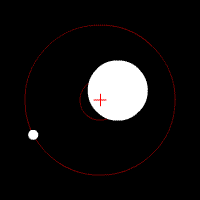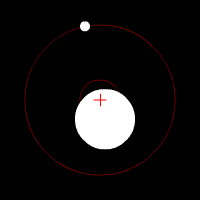
Second Kepler's law (area theorem)
- At the same time, the driving beam sweeps the object – center of gravity over the same areas.
The driving beam is the line connecting the center of gravity of a celestial body , e.g. B. a planet or moon, and the center of gravity , z. B. in a first approximation of the sun or the planet around which it moves.
A simple derivation can be made if one looks at the areas that the driving beam covers in a small period of time. In the graphic on the right, Z is the center of force. The Trabant initially moves from A to B. If its speed did not change, it would move from B to C in the next time step . It can quickly be seen that the two triangles ZAB and ZBC contain the same area. If a force is now acting in direction Z, the speed is deflected by an amount that is parallel to the common base ZB of the two triangles. Instead of C the Trabant lands at C '. Since the two triangles ZBC and ZBC 'have the same base and the same height, their area is also the same. This means that the area law applies to the two small time segments and . If one integrates such small time steps (with infinitesimal time steps ), one obtains the area theorem.
The swept area is for an infinitesimal time step
- .
Since the angular momentum is due to a central force
is constant, the area integral is straight
- .
The same swept area therefore results for the same time differences .
The second Kepler law defines both the geometric basis of an astrometric orbit (as a path in a plane) and its orbit dynamics (the behavior over time). Kepler formulated the law only for the orbit of the planets around the sun, but it also applies to non-closed orbits . In contrast to the other two laws, Kepler's second law is not limited to the force of gravity (in fact, with his anima motrix , Kepler also assumed a force), but applies in general to all central forces and movements with constant angular momentum. Kepler was only interested in a description of the planetary orbits, but the second law is already the first formulation of the law that we know today as conservation of angular momentum . The second Kepler's law can be seen as a special formulation of the angular momentum theorem, see also the law of swirl # surface theorem .
Kepler's second law also has two fundamental consequences for the movement relationships in multi-body systems, both for solar systems and for space travel: The constancy of the orbit normal vector means that elementary celestial mechanics is a flat problem. In fact, there are also deviations here due to the volumes of the celestial bodies, so that mass lies outside the plane of the orbit and the planes of the orbit precess (change their position in space). Therefore, the orbits of the planets do not all lie in one plane (the ideal solar system plane , the ecliptic ), they rather show an inclination and also perihelion rotation , and the ecliptical latitude of the sun also fluctuates . Conversely, it is relatively easy to move a spacecraft in the plane of the solar system, but it is extremely complex, for example to place a probe over the north pole of the sun.
The constancy of the surface velocity means that an imaginary connecting line between the central body, more precisely the center of gravity of the two celestial bodies, and a satellite always sweeps over the same area at the same time. So a body moves faster when it is close to its center of gravity and the slower the further it is away from it. This applies, for example, to the course of the earth around the sun as well as to the course of the moon or a satellite around the earth. A path presents itself as a constant free fall , swinging close to the center of gravity, and ascending again to the furthest culmination point of the path: The body becomes faster and faster, has the highest speed in the pericenter (point closest to the center) and then becomes slower and slower to the apocenter ( most distant point) from which it accelerates again. Seen in this way, the Keplerellipse is a special case of the crooked throw that closes in its orbit. This consideration plays a central role in space physics, where it is a matter of generating a suitable orbit with a suitably selected initial impulse (through the start): the more circular the orbit, the more uniform the orbital speed.
Third Kepler's Law
- The squares of the orbital times and two satellites around a common center are proportional to the third powers of the major semiaxes and their elliptical orbits.
or
- The squares of the periods of revolution are in the same ratio as the cubes (third powers) of the major semiaxes:
- ... third Kepler's law
Kepler used the mean distances from the sun for half of the orbit axes (in the sense of the mean of perihelion distance and apheld distance ).
- ... third Kepler's law, mass-independent formulation with Kepler's constant of the central mass ( Gaussian gravitational constant of the solar system)
In combination with the law of gravity , Kepler's third law is given for the motion of two masses and the form
- ... third Kepler's law, formulation with two masses
The approximation applies if the mass is negligibly small compared to (e.g. in the solar system). With this form one can determine the total mass of binary star systems from the measurement of the period of revolution and the distance.
Taking into account the different masses of two celestial bodies and the above formula, a more exact formulation of Kepler's third law is:
- ... third Kepler's law, formulation with three masses
Obviously, the deviation only becomes more important if both satellites differ greatly in their masses and the central object has a mass that does not deviate significantly from that of one of the two satellites.
The third Kepler law applies to all forces that decrease quadratically with the distance, as one can easily deduce from the scale consideration. In the equation
appears in the third power and as a square. A scale transformation thus gives the same equation if is. On the other hand, it is easy to recognize the fact that the analogue of Kepler's Third Law of closed paths in a force field for any currently is.
See also
- Hohmann-Transfer , the connecting line between two Kepler orbits in space travel
- Specific angular momentum , relatively simple derivation of Kepler's laws based on the conservation of angular momentum
literature
- Johannes Kepler: Astronomia nova aitiologetos seu Physica coelestis . In: Max Caspar (Ed.): Collected works . tape 3 . C. H. Beck, Munich 1938.
- Johannes Kepler: Harmonices Mundi Libri V . In: Max Caspar (Ed.): Collected works . tape 6 . C. H. Beck, Munich 1990, ISBN 3-406-01648-0 .
- Andreas Guthmann: Introduction to celestial mechanics and ephemeris calculus . BI-Wiss.-Verlag, Mannheim 1994, ISBN 3-411-17051-4 .
Web links
- Walter Fendt: 1. Kepler's law , 2. Kepler's law (HTML5 apps).
- Kepler's Laws ( LEIFI ).
- Joachim Hoffmüller: 2. Kepler's law (area theorem): Understand proof with dynamic worksheets. Geometric-descriptive proof according to Newton, without higher mathematics ( Java applet ).
- Video: Kepler's laws of planetary motions . Institute for Scientific Film (IWF) 1978, made available by the Technical Information Library (TIB), doi : 10.3203 / IWF / C-1286 .
Individual evidence
- ↑ Thomas S. Kuhn: The Copernican Revolution. Vieweg, Braunschweig 1980, ISBN 3-528-08433-2 .
- ^ Carl B. Boyer: Note on Epicycles & the Ellipse from Copernicus to Lahire . In: Isis . tape 38 , 1947, pp. 54-56 . The Kepler sentence quoted here in italics is reproduced there as a direct translation.
- ↑ Arthur Koestler: Die Nachtwandler: The history of our world knowledge . Suhrkamp, 1980.
- ↑ Bruce Stephenson: Kepler's physical astronomy . Springer Science & Business Media Vol. 13, 2012.
- ↑ Martin Holder: The Kepler Ellipse . universi, Siegen 2015 ( online [PDF; accessed November 1, 2017]).
- ^ Curtis Wilson: How Did Kepler Discover His First Two Laws? In: Scientific American . tape 226 , no. 3 , 1972, p. 92-107 , JSTOR : 24927297 .
- ↑ Guthmann, § II.2.37 Solution of Clairot's equation: The case e <1. P. 81 f.
- ↑ Guthmann, § II.1 One- and two-body problem. Introduction, pp. 64 f. And 30. Clairot's equation. P. 71 ff.
- ↑ Guthmann, § II.1.26 The area set. P. 66 f.
- ↑ Guthmann, § II.5 orbital dynamics of the Kepler problem. P. 108 ff.
- ↑ David L. Goodstein, Judith R. Goodstein: Feynman's lost lecture: The movement of planets around the sun . Piper Verlag GmbH, Munich 1998.
- ^ LD Landau and EM Lifshitz: Mechanics . 3rd Edition. Butterworth-Heinemann, Oxford 1976, ISBN 978-0-7506-2896-9 , pp. 22-24 (English).
- ↑ J. Wess: Theoretical Mechanics. Jumper. Chapter on the two-body problem.






![\ left ({\ frac {dr} {d \ phi}} \ right) ^ {2} = 2m {\ frac {r ^ {4}} {L ^ {2}}} \ left [E + {\ frac { GMm} {r}} - {\ frac {L ^ {2}} {2mr ^ {2}}} \ right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/0cfc63d521b89f242eedcd331d5af6c63c2a9bdf)

























![[- \ Delta t, 0]](https://wikimedia.org/api/rest_v1/media/math/render/svg/c9545704e10ee81c14d29d94d958e92d587e3abb)
![[0, \ Delta t]](https://wikimedia.org/api/rest_v1/media/math/render/svg/c373337a0dabc8a562b63b15537cfe8bc38ccabb)























