Hohmann transfer

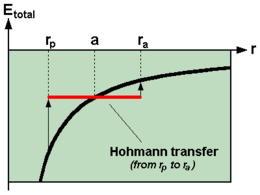
The Hohmann-Bahn (yellow) connects two circular tracks, e.g. B. a near-earth orbit (green, ) with the geostationary orbit (red ,, not to scale). ${\displaystyle r_{e}=R}$ ${\displaystyle r_{a}=R'}$

The Hohmann transfer is an energetically favorable transition between two orbits around a dominant celestial body. The transfer ellipse ( Hohmann path ) runs tangential to both the starting path and the target path; there is one each impulse (kick burn) needed to adjust the speed ( or ). Such a sketch can already be found by Ziolkowski around 1911 . In 1925, Walter Hohmann considered this transfer to be optimal. This is also the case for coplanar , circular starting and target paths with a radius ratio below 11.94; for more extreme conditions and paths that are strongly inclined or even counter-rotating, a bi-elliptical transfer is energetically more favorable. ${\displaystyle \Delta v_{e}}$ ${\displaystyle \Delta v_{a}}$

The task of moving satellites from near-earth to geostationary orbit , see geostationary transfer orbit, comes close to the idealizing prerequisites . For flights to the moon or neighboring planets, the central field approximation is less good - with swing-by maneuvers and time-consuming detours, fuel can be saved compared to the analytically found Hohmann transfer.

Calculation using the example of transfer to the geostationary orbit

→ Main article : Geostationary transfer orbit

To position satellites in a geostationary manner, they are often first placed in a circular, low orbit, Low Earth Orbit (LEO) , see (1) in the graphic. A first impulse ( ) brings the satellite onto the elliptical Hohmann orbit (2), the apogee of which is in the range of the target orbit (3). There another impulse ( ) increases the perigee of the orbit, which is thus circular again. ${\displaystyle \Delta v_{e}}$ ${\displaystyle \Delta v_{a}}$

Speeds

Total energy balance at the Hohmann transition between two circular paths with the start radius and the end radius . The black line indicates the energy for circular orbits with the respective radius. ${\displaystyle r_{e}}$ ${\displaystyle r_{a}}$

According to the Vis-Viva equation , the velocity v (r) of a body at the location r on an elliptical orbit with the semi-major axis a around the earth is:

(1) ${\displaystyle v={\sqrt {\mu \cdot \left({\frac {2}{r}}-{\frac {1}{a}}\right)}}}$

with , where the earth mass and the gravitational constant are. If the perigee or LEO radius, the apogee or GEO radius and the major semi-axis of the transfer ellipse are used, the following equations apply to the initial velocity v _LEO , perigee velocity v _e , apogee velocity v _a and final velocity v _GEO : ${\displaystyle \mu =M\cdot \gamma }$ ${\displaystyle M}$ ${\displaystyle \gamma }$ ${\displaystyle r_{\mathrm {e} }}$ ${\displaystyle r_{\mathrm {a} }}$ ${\displaystyle a={\frac {r_{\mathrm {e} }+r_{\mathrm {a} }}{2}}}$

(2) ${\displaystyle v_{\mathrm {LEO} }={\sqrt {\frac {\mu }{r_{\mathrm {e} }}}}}$

(3) ${\displaystyle v_{\mathrm {e} }={\sqrt {\mu \cdot \left({\frac {2}{r_{e}}}-{\frac {1}{a}}\right)}}>v_{\mathrm {LEO} }}$

(4) ${\displaystyle v_{\mathrm {a} }={\sqrt {\mu \cdot \left({\frac {2}{r_{a}}}-{\frac {1}{a}}\right)}}<v_{\mathrm {GEO} }}$

(5) . ${\displaystyle v_{\mathrm {GEO} }={\sqrt {\frac {\mu }{r_{\mathrm {a} }}}}}$

numbers

The following values ​​are given:

${\displaystyle r_{\mathrm {LEO} }=r_{\mathrm {e} }=6.678\,\mathrm {km} }$

measured from the center of the earth at an initial altitude of 300 km

${\displaystyle r_{\mathrm {a} }=r_{\mathrm {GEO} }=42.164\,\mathrm {km} }$

${\displaystyle \mu =398.600\,\mathrm {km} ^{3}/\mathrm {s} ^{2}}$

Then the path speeds calculated according to the above equations are:

(6) ${\displaystyle v_{\mathrm {LEO} }=7{,}73\,\mathrm {km} /\mathrm {s} }$

(7) ${\displaystyle v_{\mathrm {e} }=10{,}15\,\mathrm {km} /\mathrm {s} }$

(8th) ${\displaystyle v_{\mathrm {a} }=1{,}6\,\mathrm {km} /\mathrm {s} }$

(9) ${\displaystyle v_{\mathrm {GEO} }=3{,}07\,\mathrm {km} /\mathrm {s} }$

This results in the two required changes in speed.

For the transition from the LEO to the transfer ellipse: ${\displaystyle \Delta v_{e}=v_{\mathrm {e} }-v_{\mathrm {LEO} }=2{,}47\,\mathrm {km} /\mathrm {s} }$

For the transition from the transfer ellipse to the GEO: ${\displaystyle \Delta v_{a}=v_{\mathrm {GEO} }-v_{\mathrm {a} }=1{,}46\,\mathrm {km} /\mathrm {s} }$

Energy expenditure depending on the radius ratio

the change in speed required for the Hohmann transfer as a function of the speed ratio of the source and destination orbit

The ellipse of the Hohmann transfer is described by the speeds of the starting and target circular paths . In order from an initial orbit to pass into the ellipse and back into a circular orbit at the goal to arrive, two bursts or two speed changes , necessary. In order to consider the required energy expenditure, the entire difference can then also be considered. The transfer ellipse is described by the semi-axis . ${\displaystyle r_{e}}$ ${\displaystyle r_{a}}$ ${\displaystyle \Delta v_{e}}$ ${\displaystyle \Delta v_{a}}$ ${\displaystyle \Delta {v}=\Delta {v}_{a}+\Delta {v}_{e}}$ ${\displaystyle {\frac {r_{a}+r_{e}}{2}}{\text{ mit }}r_{a}>r_{e}>0}$

${\displaystyle \Delta v_{e}=v_{e}\left({\sqrt {\frac {2r_{a}}{r_{e}+r_{a}}}}-1\right)}$,

${\displaystyle \Delta v_{a}=v_{a}\left(1-{\sqrt {\frac {2r_{e}}{r_{a}+r_{e}}}}\right)}$

For further discussion it is useful to consider the dimensionless quantity . The auxiliary variable then results in: ${\displaystyle {\frac {\Delta {v}}{v_{e}}}={\frac {\Delta {v}_{e}}{v_{e}}}+{\frac {\Delta {v}_{a}}{v_{e}}}={\frac {\Delta {v}_{e}}{v_{e}}}+{\frac {r_{e}}{r_{a}}}{\frac {\Delta {v}_{a}}{v_{a}}}}$ ${\displaystyle R={\frac {r_{a}}{r_{e}}}>0}$

${\displaystyle {\frac {\Delta {v}}{v_{e}}}=\left(1-{\frac {1}{R}}\right)\left({\frac {2R}{1+R}}\right)^{\frac {1}{2}}+\left({\frac {1}{R}}\right)^{\frac {1}{2}}-1}$

When the Hohmann transfer proves to be useful can be determined through a more detailed discussion of the speed change. An extreme value of the above formula can be determined by deriving it and equating it with zero :

${\displaystyle {\frac {d(\Delta {v}/v_{e})}{dR}}={\frac {1}{R^{2}}}\left[{\frac {2R}{1+R}}\right]^{\frac {1}{2}}+{\frac {R-1}{R(1+R)^{2}}}\left[{\frac {2R}{1+R}}\right]^{-{\frac {1}{2}}}-{\frac {1}{2R^{\frac {3}{2}}}}=0}$

${\displaystyle \Leftrightarrow R^{3}-15R^{2}-9R-1=0}$

The only sensible solution arises for . The ratio for maximum is therefore by the context: given. Furthermore, the derivative is strictly monotonically increasing for each . This means that the energy expenditure is reduced again for each larger ratio . ${\displaystyle R=15{,}582}$ ${\displaystyle r_{a}/r_{e}}$ ${\displaystyle r_{e}\cdot 15{,}582=r_{a}}$ ${\displaystyle R>15{,}582}$ ${\displaystyle r_{a}/r_{e}}$

example

Transfer orbit to Mars

Transfer Earth → Mars

Mars is closest to Earth in opposition . However, a spaceship or space probe can only use this geometric proximity with great effort, since in this case it would have to be approached against the orbit movement of the earth.

According to Hohmann, on the other hand, the most energetically favorable transfer is the one in which the spacecraft reaches Mars in conjunction with the position on earth from which it started. In the figure on the left, the spacecraft starts on earth at (1) and reaches Mars at position (3), while the sun is in one of the focal points of the transfer orbit (yellow) all the time. The double semi-axis of the transfer ellipse is the sum of the distance between Earth and Sun and Sun and Mars . According to Kepler's third law, this results in half a period of eight and a half months.

Transfer orbit of a Mars probe

The picture on the right shows the transfer orbit of the Mars Reconnaissance Orbiter , which requires more energy than the Hohmann orbit (the transition orbit leads over the Mars orbit), but the travel time is only seven months.

Weak stability boundary

If the target planet is to be approached at the lowest possible speed, the so-called weak stability boundary method offers another energy gain. The probe is slowed down by maneuvering it along libration points. A first useful orbit calculation was carried out in 1986. The ESA probe SMART-1 approached the moon using this method.

See also

• Hill's equations

Individual evidence

1. ↑ Walter Hohmann: The accessibility of the heavenly bodies - studies on the space problem. Oldenbourg, Munich 1925
2. ↑ Shane D. Ross: The Interplanetary Transport Network , American Scientist 94, 2006, pp. 230-237, doi : 10.1511 / 2006.3.230 ( online ).

literature

• Pedro Ramon Escobal: Methods of Astrodynamics . John Wiley & Sons, 1969, ISBN 978-0-471-24528-5 .
• Palmore: An Elementary Proof of the Optimality of Hohmann Transfer . Journal of Guidance, 1984.

Web links

• Assessment of Mission Design Including Utilization of Libration Points and Weak Stability Boundaries (PDF; 9.3 MB)
• Derivation of the formula for the orbital velocity v of a body moving in a force field on an elliptical path
• Interplanetary Trajectories-Hohmann Transfer Orbits , jpl.nasa.gov, accessed November 4, 2011