Delta v

Delta v ( ) is the change (delta or Δ) in the speed ( vector ) and is specified in distance per time (m / s or km / h). It results from the subtraction of two speeds, ${\ displaystyle \ Delta v}$ ${\ displaystyle {\ overrightarrow {v}}}$

{\ displaystyle \ Delta v = | {\ overrightarrow {v_ {2}}} - {\ overrightarrow {v_ {1}}} |}

,

where is the speed before an event and the speed after the event. Since the difference between the speed vectors is used to calculate, changes in direction are also taken into account, in which the amount of speed remains the same. ${\ displaystyle {\ overrightarrow {v_ {1}}}}$ ${\ displaystyle {\ overrightarrow {v_ {2}}}}$ ${\ displaystyle \ Delta v}$

Space dynamics

In space travel , delta v, often written out instead of with symbols, is a measure of the ability of a spacecraft to perform maneuvers. In the simplest case, without the influence of gravitation , Delta v is the integral of the amounts of all speed changes along the desired trajectory . This integral is invariant to the mass of the spacecraft performing the maneuver, as well as to technical details of its propulsion system. The invariance of the size has obvious advantages, so that instead of mass, thrust and fuel supply for spacecraft, the total delta v ( ) that the spacecraft is capable of with the available fuel resources is given. If the value of the remainder is reached , all fuel has been used up and no more course changes are possible. ${\ displaystyle \ Delta v _ {\ mathrm {max}}}$ ${\ displaystyle \ Delta v _ {\ mathrm {max}} = 0}$

In the gravitational field, e.g. B. during takeoff or swing-by , the delta v to be generated by the spacecraft does not correspond directly to a change in speed, but can still be calculated as a variable. In the atmosphere and in a non-free fall situation, however, it also depends on the aerodynamic properties of the vehicle and the time it takes for the spacecraft to enter a stable orbit , i.e. H. a free fall situation to arrive. For a start in a low earth orbit it is necessary to increase the speed from the rotational speed on the earth's surface to the orbital speed. This proportion is invariant to the design of the spacecraft. In addition, there are typically air resistance and the overcoming of earth's gravity. The balance is reduced by the earth's rotation by a maximum of 465 m / s if the start at the equator takes place with an inclination of 0 ° in an easterly direction. ${\ displaystyle \ Delta v = 7 {,} 8 \, \ mathrm {km / s}}$ ${\ displaystyle \ Delta v = 1 {,} 5 {\ text {to}} 2 \, \ mathrm {km / s}}$

It should be noted that with this specification, the weight of the payload (weight of the people on board / the spacecraft) has an influence on the available delta v of a spaceship, since the available delta v decreases with an increase in mass and the resulting increased inertia . In other words: If the astronauts had packed too many moonstones for the Apollo missions, the delta v of the ascent stage required to reach the mother ship would remain the same, but the delta v that would be available would decrease and the value of what was needed Fall below Delta v, which would make the ascent level too difficult and the mother ship would no longer have been accessible.

The of the fully fueled Apollo spacecraft was, for example at maximum payload 2,804 m / s, that of the Lunar Module 4,690 m / s. ${\ displaystyle \ Delta v _ {\ mathrm {max}}}$

Typical delta v for orbital and interplanetary maneuvers

Delta v in km / s for various maneuvers from the earth to the moon and mars

Stabilization maneuvers	Track height (km)	Delta v (m / s per year)
Stabilization maneuvers	Track height (km)	Type.	Max.
Position stabilization		<50-55
Altitude stabilization (air resistance)	<400-500	<25	<100
	<500-600	< 05	< 025
	> 600		< 007.5

One-time maneuvers	Delta v (m / s)
Position control	2 06
Rotation control	5-10
Relief of the position stabilization gyro	2 06
Separation from the starting stage	5-10
Uncoupling a spaceship from the ISS by means of spring force	0.12

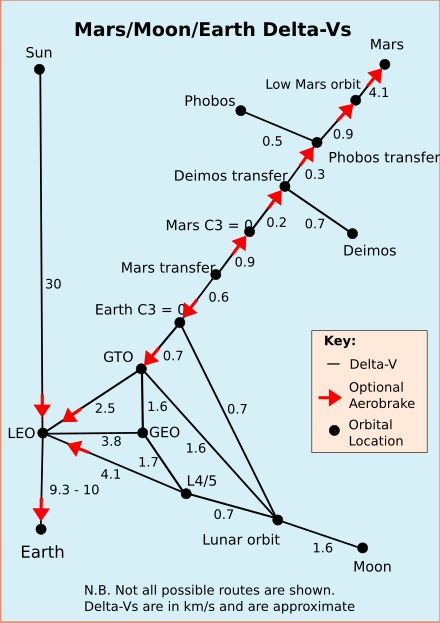
Maneuver to change orbit (see graphic on the right)		Delta v (m / s)
from	to	Delta v (m / s)
Surface of the earth	Low Earth Orbit (LEO)	9,300-10,000
Low Earth Orbit	Geostationary Transfer Orbit (GTO)	2,500
Geostationary transfer orbit	Geosynchronous Orbit (GEO, GSO)	1,500
Perigee of the geostationary transfer orbit	Escape route	0.700
Escape route	Low lunar orbit	0.700
Escape route	Mars transfer orbit	0.600
Low Earth Orbit	Mars surface	4,800
Low Earth Orbit	Escape path from the solar system	8,700
Low lunar orbit	Lunar surface	1,600

Accident mechanics

In the event of a traffic accident , for example a collision between two cars , a collision- related change in speed (Δv) (for each vehicle) can be calculated. Δv is considered to be the main measure of the severity of the collision , as it is related to the impact forces of the collision and the deceleration of the vehicle. As a rule, the greater the change in speed during a collision, the greater the risk of injury to occupants.

A typical example is the rear-end collision , which usually leads to a positive change in the speed of the vehicle ahead or stationary, i.e. this vehicle is accelerated as a result of the collision. Depending on the severity of the impact, there is a risk of injury for the occupants there, especially for the cervical spine in the form of whiplash .

Web links

Delta-v calculator for simple rockets (English)

Individual evidence

↑ Chris Gebhardt: Soyuz MS-03 undocks, conducts rare two-person landing. nasaspaceflight.com, June 2, 2017, accessed on February 27, 2018 (English): "The push Soyuz received from the springs at undocking imparted a delta-V change of 0.12 m / s"

[1] Chris Gebhardt: Soyuz MS-03 undocks, conducts rare two-person landing. nasaspaceflight.com, June 2, 2017, accessed on February 27, 2018 (English): "The push Soyuz received from the springs at undocking imparted a delta-V change of 0.12 m / s"