Swing-by
The English term swing-by - also known as slingshot, gravity assist (GA), deflection of gravity or swing- past maneuver - describes a method of space travel in which a relatively light spacecraft (such as a space probe ) is close to a much larger body (such as a planet ) flies by. In this variant of a flyby , the direction of flight of the probe is changed, and its speed can also be increased or decreased. A swing-by maneuver can also be combined with an engine ignition. In the case of very close flyby, a significantly higher fuel efficiency can be achieved under certain circumstances (see Oberth Effect ).
The swing-by effect also occurs when a comet, an asteroid, or (as it probably happened in the early history of the solar system) a lighter planet passes a heavier planet in its gravitational field. If the mass of the lighter planet is not negligibly small compared to the heavier one, the heavier planet will also change its orbit noticeably.
principle
- Time course of the speed during swing-by
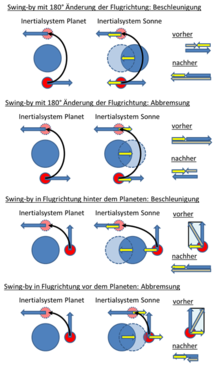
When a probe moves through the gravitational field of a planet, it is deflected by its gravitational pull. In relation to the planet, the absolute value of the speed of the probe does not change at infinite distance from the planet, i.e. H. the orbital energy of the spacecraft relative to the planet remains constant. However, the direction of the speed is changed by the deflection. Physically, this represents an acceleration , i. H. a change in speed. The planet also moves around the sun, so does the reference system related to it. This reduces or increases the speed of the probe in the frame of reference that is used to describe the planetary motion. The relative speed of the probe to the planet must be added vectorially with the speed of the planet in order to obtain the speed of the probe in relation to the sun.
The planet's gravitational field is responsible for the acceleration of the planet-centric velocity vector, which is realized as a change in direction. During the swing-by, the gravitational forces between the probe and the planet couple the two movements and enable an exchange of orbital energy between the two. Due to the significantly larger mass of the planet compared to the spacecraft and the associated significantly higher energy, the effects on the planet's orbit cannot be measured, while the orbital energy of the probe can change considerably. This change in orbital energy would have to be achieved without swing-by using fuel, which is why performing such maneuvers is fuel-efficient and is therefore advantageous for carrying out missions.
Effects
Basically, the following effects result:
- Change of the amount of speed in the higher-level reference system, d. H. the orbital energy of the spacecraft
- Change of flight direction within the orbit plane of the reference system (e.g. the ecliptic ) for sighting new targets
- Change of the path level, e.g. B. Leaving the ecliptic
Swing-by maneuvers can thus serve to save fuel on interplanetary flights and therefore also reduce costs. The travel time can be shortened by the speed gained, but also increase as a result of detours. On the target planet, the travel speed can be reduced with swing-by on a satellite (moon) in order to bring the probe into orbit.
Comparison with impact processes
To simplify matters, the elastic impact of two bodies can be used to illustrate , for example the frontal contact of a table tennis ball with a table tennis racket. If the table tennis racket rests immobile, the ball rebounds idealized (i.e. without taking into account friction, angle of attack of the racket, etc.) at the same speed. If the player moves the bat towards the ball, it will bounce back (from the viewer's point of view) at a higher speed; conversely, the player can slow down the ball by "taking back" the racket. From the “point of view” (inertial system) of the club, it always rebounds at the same speed, otherwise it would not be an elastic shock.
If the ball and racket do not meet head-on, the lateral speed component must also be taken into account; It is the same with swing-by, as the space probe does not hit the planet head-on. With swing-by, the interaction takes place over a longer period of time, but the basic principle is the same.
Route planning
Since in reality there is at least a three-body problem (e.g. probe, planet and sun), the changes in orbit cannot be calculated analytically, but only numerically more precisely. Since the flight angle and the speed depend on each other after the passage, the scope for the distance and the position of the next target object is limited. If several targets are specified and / or restricted to a certain approach path and speed at the target, a system of equations is created that is numerically checked for solutions. The solutions ( trajectories ) mostly result in only narrow starting time windows on the order of days or weeks, which for the same mission goals can be years or many decades apart. The launch speed from the earth and thus the cost of the rockets, as well as the duration of the mission are also specifications or results of the calculations.
history
Swing-by maneuvers to change the direction of flight took place in the early days of space travel, for example with the Luna 3 probe (1959), which was the first to circle the moon and set course for earth again. A swing-by maneuver was also used in Apollo 13 (1970) to fly around the moon in a loop and return directly. With the solar probe Ulysses (1990) a swing-by at Jupiter was used to change the inclination in order to leave the plane of the ecliptic.
Michael Minovitch , who worked at the Jet Propulsion Laboratory , discovered in 1961 that space probes can be given additional speed by swing-by . Previously, it had been considered impossible that conventional rocket technology could ever reach the planets of the outer solar system. The reason for this is the theoretically assumed energetic minimum that is given by a Hohmann transfer and the fact that, according to the basic rocket equation, the required launch mass of the spacecraft grows exponentially with the required final speed.
The first interplanetary probes to use this technology were Pioneer 10 (1972: Earth → Jupiter → interstellar space), Pioneer 11 (1973: Earth → Jupiter → Saturn → interstellar space) and Mariner 10 (1973: Earth → Venus → Mercury ) . Swing-by was of particular importance for the two Voyager probes (1977): Due to a planetary constellation that only occurs every 176 years, Voyager 2 was able to visit the planets Jupiter, Saturn, Uranus and Neptune one after the other , as well as its sister probe Voyager 1 , which visited Jupiter and Saturn, reached the third cosmic speed that brought them into interstellar space.

In the meantime, space probes have been launched with increasingly complex trajectories : the Jupiter probe Galileo (1989) flew past Venus and twice past the Earth, the Saturn probe Cassini-Huygens (1997) twice past Venus, Earth and Jupiter. The Rosetta mission (2004) reached Comet Churyumov-Gerasimenko via several swing-by maneuvers on Earth and Mars , and the Parker Solar Probe (2018) uses seven fly-bys to slow down Venus. After a total of nine swing-bys to Earth, Venus and Mercury, BepiColombo (2025) is expected to enter orbit around Mercury.
See also
literature
- B. Stanek: Space Dictionary. Halwag Verlag, Bern (1983), ISBN 3-444-10288-7 , pp. 331-334.
- Ernst Messerschmid, Stefanos Fasoulas: Space systems: An introduction with exercises and solutions. Springer Verlag, Berlin Heidelberg 2013, ISBN 978-3-662-09674-1 , pp. 142–150 ( limited preview in the Google book search).
Web links
- Michael Müller: Swing-by. In the archive of: Wissensnishorizont.de.
Individual evidence
- ↑ Stefan Deiters: Solar System. Were there once five gas giants? astronews.com, November 16, 2011, accessed April 16, 2014 .
- ↑ Laura Hennemann: Solar system. The outcast planet. sterne-und-weltraum.de, November 15, 2011, accessed on April 16, 2014 . (The article names the source: arxiv : 1109.2949 )
- ^ A Gravity Assist Primer. JPL / NASA, archived from the original on July 26, 2016 ; accessed on April 16, 2014 (English).
- ↑ Luna 3 orbit. The Planetary Society, accessed December 17, 2018 .
- ^ W. David Woods: How Apollo Flew to the Moon . Springer ( limited preview in Google Book Search).
- ^ M. Minovitch: Gravity Assist.
- ↑ a b Richard L. Dowling et al: The Effect of Gravity-Propelled Interplanetary Space Travel on the Exploration of the Solar System: Historical Survey, 1961 to 2000. (PDF) In: History of Rocketry and Astronautics, AAS History Series, Vol 28. Donald C Elder, p. 339 , accessed December 17, 2018 .
- ↑ Reiner Klingholz: Marathon in Space: the unique journey of Voyager 2 . Ullstein, 1992, ISBN 3-548-34870-X , pp. 23 .
- ↑ SP-424 Mariner Venus-Mercury Mission. At: History.NASA.gov.
- ↑ https://sci.esa.int/web/bepicolombo/-/48871-getting-to-mercury