Orbit inclination

A - celestial body
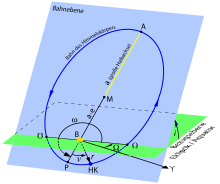
B - central object
green - reference plane (e.g. equatorial plane)
blue - orbital plane (orbital plane)
i - inclination
Ω - length of the ascending node

In celestial mechanics, the orbital inclination or inclination of a celestial body is the angle between its orbital plane and a reference plane . The orbit inclination is one of the six orbit elements of classic orbit determination and is denoted by the symbol in this context . Together with the length of the ascending node , it defines the position of the path plane in space. Orbital inclinations between 90 ° and 180 ° characterize a retrograde (opposing) orbit. ${\ displaystyle i}$

The orbital inclination of a celestial body is related to the direction of the orbital angular momentum vector of the body. By definition, this is perpendicular to the plane of the orbit. If no torque acts on the celestial body as a whole, as is the case with central forces, the orbital angular momentum and thus its direction do not change. In this case the body has a temporally unchangeable orbit plane in which it moves. Therefore, in these cases, with a fixed reference plane, the path inclination also remains constant. This is e.g. B. in the case of Kepler orbits (only two bodies in a vacuum ), and the orbit plane remains stable in its alignment under the fixed stars . In the case of gravitational disturbances by third bodies , a torque is exerted by them, so that the angular momentum vector changes. As a result, the orbit inclination, like other orbit elements, suffers small, sometimes periodic changes. The orbital elements are therefore specified as a series of oscillating terms with respect to an epoch , i.e. as an approximate solution that is valid at a certain point in time .

Reference plane

The reference plane of the orbit inclination depends on the celestial body under consideration:

In the solar system , the plane of the earth's orbit ( ecliptic ) is usually chosen, from which the orbits of the large planets and the moon deviate by only a few degrees.

For artificial terrestrial satellites , the earth's mean equatorial plane is chosen as the reference for the satellite orbit elements , orbits with an angle of inclination close to 90 ° are hot polar orbits .

The inclinations of the planetary moons of the other planets of the solar system are mostly also related to the equatorial plane of the orbiting planet. This also applies to artificial satellites of these planets ( orbiters ). For more distant moons, on the other hand, such as the earth's moon , the measurement is approximately based on the plane of the planet's orbit in the solar system. The exact representation, which also guarantees a temporally constant reference plane for “moderately distant” moons such as the large Saturn moon Iapetus , is given by the inclination with respect to the Laplace plane .

The inclination of an orbit of an exoplanet or in a multiple star system is measured from a plane perpendicular to the direct geocentric line of sight. Thus means and that we see the system directly "from above", ie the Bahnpol points to the observer, and that we have the orbital plane see directly from the "edge" ( Engl. "Edge on" ). ${\ displaystyle i = 0 ^ {\ circ}}$ ${\ displaystyle i = 180 ^ {\ circ}}$ ${\ displaystyle i = 90 ^ {\ circ}}$

literature

Andreas Guthmann: Introduction to celestial mechanics and ephemeris calculus. BI-Wiss.-Verl., Mannheim 1994, ISBN 3-411-17051-4 .
M. Schneider: Celestial Mechanics. BI-Wiss.-Verlag, Mannheim 1993.

Orbit inclination

Reference plane

literature

See also