Kepler Railway
Kepler orbits are solutions to the two-body problem of classical celestial mechanics , in which two mass points move around the common center of gravity (their barycenter ) under the influence of their mutual attraction ( gravitation ) . The shapes of the Kepler orbits are conic sections : circle , ellipse , parabola and hyperbola , with the barycentre at the focal point of the orbit.
If the barycentre is considered to be stationary, both bodies synchronously execute a similar Kepler orbit around the barycenter, whereby they always occupy opposite points to the barycenter and the ratio of their variable distances to the barycenter is always the opposite of their mass ratio. In practice, one body is often so much more massive than the other that the more massive body can also be viewed as stationary. With this consideration, the body with less mass executes a Kepler orbit around the body with greater mass. On approximate Kepler ellipses z. B. the planets , comets and asteroids around the sun , or the moon around the earth .
For the orientation of a Kepler path in space see path elements . For movement on Kepler railways see Kepler's laws . For deviations from the ideal, see railway disruption .
Details
In polar coordinates , a Kepler orbit shows the following angular dependence of the radius , i.e. the distance between the point of the path and the center of gravity :
The angle between the apsidal line and the radius vector is counted from the periapsis , which is on the right in the picture, called the true anomaly .
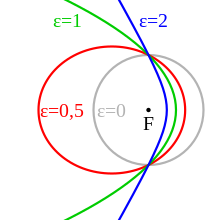
The numerical eccentricity indicates the stretching of the path:
- Circular path
- elliptical orbit
- parabolic orbit
- hyperbolic orbit.
For the open orbits (parabola and hyperbola) the domain of definition is limited to the open interval . Celestial bodies on open orbits have an unbound state to the central star . Examples are some comets that disappear from the solar system without returning after a single approach to the sun .
The paths intersect for different ones (the so - called half parameter scales the shape).
See also
Individual evidence
- ^ Franz Embacher: Elements of Theoretical Physics . tape 1 . Springer DE, 2010, ISBN 3-8348-9782-5 , p. 134 ( limited preview in Google Book search).