Polar coordinates
In mathematics and geodesy , a polar coordinate system (also: circular coordinate system ) is a two-dimensional coordinate system in which each point in a plane is defined by the distance from a given fixed point and the angle to a fixed direction.
The fixed point is called the pole ; it corresponds to the origin in a Cartesian coordinate system . The ray emanating from the pole in the specified direction is called the polar axis. The distance from the pole is usually called or and is called radius or radial coordinate, the angle is called or and is called angle coordinate, polar angle, azimuth or argument.
Polar coordinates are a special case of orthogonal curvilinear coordinates . They are useful when the relationship between two points is easier to describe in terms of angles and distances than would be the case with - and - coordinates. In geodesy, polar coordinates are the most common method for measuring points ( polar method ). In radio navigation , the principle is often referred to as " Rho-Theta " (for distance and direction measurement).
In mathematics, the angular coordinate is measured in the mathematically positive direction of rotation (counterclockwise). If a Cartesian coordinate system is used at the same time, its coordinate origin generally serves as the pole and the axis as the polar axis. The angular coordinate is measured from the axis in the direction of the axis. In geodesy and navigation, azimuth is measured clockwise from north .
history
The terms angle and radius were already used by the ancients in the first millennium BC. The Greek astronomer Hipparchus (190-120 BC) created a table of trigonometric chord functions to find the length of the chord for each angle. With the help of this basis it was possible for him to use the polar coordinates in order to be able to determine the position of certain stars. However, his work only covered part of the coordinate system.
In his treatise On Spirals , Archimedes describes a spiral line with a function whose radius changes depending on its angle. However, the work of the Greek did not yet encompass a full coordinate system.
There are various descriptions for defining the polar coordinate system as part of a formal coordinate system. The entire history on this topic is summarized and explained in the book Origin of Polar Coordinates by Harvard Professor Julian Coolidge. Accordingly, Grégoire de Saint-Vincent and Bonaventura Cavalieri introduced this concept independently of each other in the middle of the 17th century. Saint-Vincent wrote on the subject on a private basis in 1625 and published his work in 1647, while Cavalieri published his draft in 1635, with a corrected version appearing in 1653. Cavalieri initially used polar coordinates to solve a problem related to the area of the Archimedean spiral . A little later, Blaise Pascal used polar coordinates to calculate the length of parabolic angles.
In the Method of Fluxions (written 1671, published 1736) Sir Isaac Newton considers the transformation between polar coordinates to which he refers to as “Seventh Manner; For Spirals, ”(Seventh Method; For Spirals), and nine other coordinate systems.
It was followed by Jacob Bernoulli , who in the journal Acta Eruditorum (1691) used a system that consisted of a straight line and a point on this straight line, which he called the polar axis or pole . The coordinates were defined therein by the distance from the pole and the angle to the polar axis. Bernoulli's work extended to the formulation of the curvature circle of curves, which he expressed by the coordinates mentioned.
The term polar coordinates in use today was finally introduced by Gregorio Fontana and used in Italian scripts of the 18th century. George Peacock subsequently adopted this name in English in 1816 when he translated the work of Sylvestre Lacroix Differential and Integral Calculus into his language.
Alexis-Claude Clairaut, on the other hand, was the first to think about polar coordinates in three dimensions, but it was only the Swiss mathematician Leonhard Euler who succeeded in developing them .
Polar coordinates in the plane: circular coordinates
definition
The polar coordinates of a point in the Euclidean plane (plane polar coordinates) are given in relation to a coordinate origin (a point on the plane) and a direction (a ray beginning at the coordinate origin ).
The polar coordinate system is clearly defined in that an excellent point, also called a pole, forms the origin / zero point of the coordinate system. Furthermore, a ray emanating from it is marked as a so-called polar axis. Ultimately, one direction (of two possible) that is perpendicular to this polar axis must be defined as positive in order to determine the direction of rotation / the direction of rotation / the orientation. Now an angle, the polar angle, can be defined between any ray that passes through the pole and this particular polar axis. It is only unambiguous up to a whole number of revolutions around the pole, regardless of what is chosen as the angle measure for it. Any, but fixed, scaling is also carried out on the polar axis itself in order to define the radial unit length. Now a point of the plane can be clearly assigned to each pair , the first component being viewed as the radial length and the second as the polar angle. Such a pair of numbers is called the (not necessarily unique) polar coordinates of a point in this plane.
- Plane polar coordinates (with angle specifications in degrees) and their transformation into Cartesian coordinates
The coordinate , a length, is referred to as the radius (in practice also as a distance) and the coordinate as the (polar) angle or, in practice (occasionally) also as the azimuth .
In mathematics, the counterclockwise angle is usually defined as positive when looking vertically from above onto the plane (clock) . So goes the direction of rotation of the right to above (and further to the left ). The preferred angle unit is the radian , because it is then the most elegant to handle analytically. The polar axis typically points to the right in graphic representations of the coordinate system .
Conversion between polar coordinates and Cartesian coordinates
Conversion of polar coordinates into Cartesian coordinates
If you choose a Cartesian coordinate system with the same origin as the polar coordinate system, with the -axis in the direction of the polar axis, and finally the positive -axis in the direction of the positive direction of rotation - as shown in the figure above on the right - the result for the Cartesian Coordinates and a point:
Conversion of Cartesian coordinates into polar coordinates
The conversion of Cartesian coordinates into polar coordinates is somewhat more difficult because, from a mathematical point of view, one is always dependent on a trigonometric inverse function (which does not cover the entire value range of the full angle) . First, however, the radius to the Pythagorean theorem simply be calculated as follows:
When determining the angle , two special features of the polar coordinates must be taken into account:
- The angle for is not uniquely determined, but could take on any real value. It is often defined as 0 for a clear transformation rule. The following formulas are given to simplify their derivation and presentation under the assumption .
- For , the angle is only determined up to integer multiples of , since the angles and (for ) describe the same point. For the purpose of a simple and unambiguous transformation rule, the angle is restricted to a half-open interval of length . Usually, the intervals or are selected depending on the area of application .
Any of the equations can be used to calculate
to be used. However, the angle is not clearly determined by this, not even in the interval or , because none of the three functions , and is injective in these intervals . The last equation is also not defined for. A distinction between cases is therefore necessary, which depends on the quadrant in which the point is located, i.e. on the signs of and .
Calculation of the angle in the interval (−π, π] or (−180 °, 180 °]
With the help of the arctangent , the interval or can be determined as follows :
Some programming languages (so first Fortran 77 ) and application programs (such as Microsoft Excel ) offer an arctangent function with two arguments , which takes the presented case distinctions internally and calculates it for any values of and .
One arrives at the same result if one interprets the point in the Cartesian plane as a complex number and the angle
calculated using the Argument function .
With the help of the arccosine , only two case distinctions can be made:
By taking advantage of the fact that a center angle in a circle is always twice as large as the associated circumferential angle , the argument can also be calculated with the help of the arctangent function with fewer case distinctions:
Calculation of the angle in the interval [0, 2π) or [0, 360 °)
The calculation of the angle in the interval or can in principle be carried out in such a way that the angle is first calculated in the interval as described above and, only if it is negative, is increased by:
By modifying the first formula above, the following can be determined directly in the interval :
In this case too, the arccosine formula makes do with only two case distinctions:
Shifting the angle
In geodetic or other calculations, azimuths with values outside the usual interval with the lower limit (or also ) can result. the equation
shifts to the desired interval, so that . Here, the rounding off to the nearest integer floor function , ie for every real is the largest integer that is not greater than is.
Functional determinant
From the formulas for converting polar coordinates into Cartesian coordinates, one obtains for the functional determinant as the determinant of the Jacobi matrix :
Surface element
With the functional determinant we get for the surface element in polar coordinates:
As the adjacent picture shows, the surface element can be interpreted as a differential rectangle with width and height .
Line element
From the transformation equations above
consequences
The following applies to the Cartesian line element
what follows in polar coordinates:
Speed and acceleration in polar coordinates
To do this, the movement is broken down into a radial and a perpendicular “transverse” component. The following applies to the velocity vector
with the unit vectors and .
The following applies to acceleration
Spatial polar coordinates: cylindrical coordinates and spherical coordinates
Cylindrical coordinates
Cylinder coordinates or cylindrical coordinates are essentially planar polar coordinates that are supplemented by a third coordinate. This third coordinate describes the height of a point vertically above (or below) the plane of the polar coordinate system and is generally referred to as. The coordinate no longer describes the distance of a point from the origin of the coordinate, but rather from the axis.
Conversion between cylindrical coordinates and Cartesian coordinates
If you align a Cartesian coordinate system so that the -axis coincide, the -axis points in the direction and the angle increases from the -axis to the -axis (directed to the right), then the following conversion formulas result:
For the conversion of Cartesian coordinates into cylindrical coordinates, the same formulas result for and as for polar coordinates.
Basis vectors
The basis vectors , and are orthonormal to one another and in this order form a right system.
Functional determinant
The addition of the straight-line coordinates has no influence on the functional determinant:
Hence the following results for the volume element :
This also corresponds to the square root of the amount of the determinant of the metric tensor , with which the coordinate transformation can be calculated (see Laplace-Beltrami operator ).
Vector analysis
The following representations of the Nabla operator can be used in the given form directly on scalar or vector-valued fields in cylindrical coordinates. The procedure here is analogous to vector analysis in Cartesian coordinates.
gradient
The representation of the gradient is transferred from Cartesian to cylindrical coordinates as follows:
divergence
In the case of divergence , there are additional terms that result from the derivatives of the , and dependent unit vectors:
rotation
The representation of the rotation is as follows:
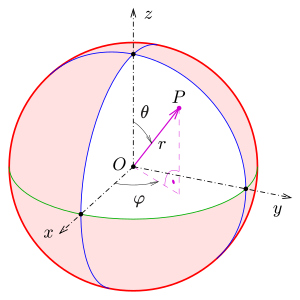
Spherical coordinates
Spherical coordinates are essentially plane polar coordinates that are supplemented by a third coordinate. This is done by specifying an angle for the third axis. This third coordinate describes the angle between the vector to the point and the axis. is zero if and only if lies in the -axis.
n -dimensional polar coordinates
It is also possible to generalize the polar coordinates with for a -dimensional space with Cartesian coordinates for . To do this, one introduces another angle for each new dimension (inductive structure via the same) , which indicates the angle between the vector and the new, positive coordinate axis for . Using the same procedure, the angular coordinate of the 2-dimensional space can be constructed in a consistent manner by means of inductive means from the number line, provided that negative values, i.e. completely , are also permitted for the radial coordinate .
Conversion into Cartesian coordinates
A rule for converting these coordinates into Cartesian coordinates would then be:
As can be proven, these polar coordinates go over into the ordinary polar coordinates for the case and into the spherical coordinates.
Functional determinant
The functional determinant of the transformation of spherical coordinates into Cartesian coordinates is:
Thus the -dimensional volume element is:
Note: -dimensional cylindrical coordinates are simply a product / composition of -dimensional spherical coordinates and -dimensional Cartesian coordinates with and .
Web links
Individual evidence
- ^ Michael Friendly: Milestones in the History of Thematic Cartography, Statistical Graphics, and Data Visualization. (No longer available online.) Archived from the original on September 25, 2006 ; Retrieved September 10, 2006 . Info: The archive link was inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice.
- ^ A b Julian Coolidge: The Origin of Polar Coordinates . In: American Mathematical Monthly . No. 59 , 1952, pp. 78-85 ( www-history.mcs.st-and.ac.uk ).
- ↑ C. B. Boyer: Newton as an Originator of Polar Coordinates . In: American Mathematical Monthly . No. 56 , 1949, pp. 73-78 .
- ↑ Jeff Miller: Earliest Known Uses of Some of the Words of Mathematics. Retrieved August 30, 2009 .
- ^ David Eugene Smith: History of Mathematics . tape 2 . Ginn and Co., Boston 1925, p. 324 .
- ^ A b Herbert Amann, Joachim Escher: Analysis III. Birkhäuser 2008, ISBN 978-3-7643-8883-6 , p. 205 ( limited online copy in Google Book Search USA ).


















![(- \ pi, \ pi]](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fbb1843079a9df3d3bbcce3249bb2599790de9c)







![{\ displaystyle (-180 ^ {\ circ}, 180 ^ {\ circ}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/52564e11cb8ecd24997d7929ef3ff9a87052b335)





















































![\ theta \ in [0, \ pi]](https://wikimedia.org/api/rest_v1/media/math/render/svg/c833964ea08aa30df8b6f56664461a5499b38144)






![\ vartheta_ {n-2} \ in [0, \ pi]](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd757b4fc3635a37579afba4382be3d4cda87789)


![{\ displaystyle \ varphi = \ vartheta _ {0} \ in [0, \ pi]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/049d26ceee7c1903d4aefcec69374863275f25f7)









