Radians (unit)
| Physical unit | |
|---|---|
| Unit name | Radians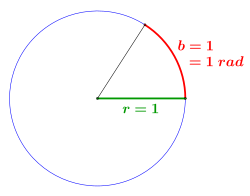
|
| Unit symbol | |
| Physical quantity (s) | Flat angle |
| Formula symbol | |
| dimension | |
| system | International system of units |
| In SI units | |
| Named after | Latin radius , "ray" |
| See also: angular dimensions | |
The radian (unit symbol: rad ) is an angular measure in which the angle is given by the length of the corresponding circular arc in the unit circle . Due to the consideration of the arc to indicate the angle of the reference "is in radians " also arc angle called. The arc length of a given angle is proportional to the radius . On a circle with a radius of 5 cm, an angle of 1 rad marks an arc of 5 cm. The full circle (360 °) has the arc length , so the full angle is rad.
In many calculations in physics and mathematics , the radian measure is the most useful angle measure, see for example angular velocity and sine and cosine .
In the International System of Units (SI), radians are the special name for the coherent, derived SI unit m / m with the dimension number . It is therefore an auxiliary unit of measurement and can simply be replaced by 1 in calculations, i.e. H. 1 rad = 1. The unit can be combined with SI prefixes , e.g. B. mrad for milliradians .
In practice, this is trailing unit symbol rad often then omitted when the angular dimension as a multiple of specified since then confusion with the data in degrees ° or gon is unlikely.
Conversion between radians and degrees
| Degree | Radians |
|---|---|
Scientific pocket calculators calculate angle functions either in degrees or in radians, sometimes also in gons , where the full angle is 400 gon. The calculation modes on most pocket calculators are called "DEG" (from English degree for degree) for the degree, "RAD" for the radian measure and "GRA" or "GRAD" for the gon angle, and can sometimes be accessed via a combination key " DRG “(from the first letters of the units) switchable.
Trigonometric functions in mathematical libraries for programming languages and in programs for spreadsheets usually use the radian measure, and degrees therefore usually have to be converted. The full angle is 2 radians or 360 degrees , therefore:
or:
So the factor for converting radians to degrees is
Examples:
Historical
In the SI, it was initially left open whether radians and steradian are derived units or base units; the class of “complementary units” was created for both. In 1980 the CIPM recommended that these supplementary units be interpreted as derived. This was followed in 1995 by the 20th CGPM and resolved in resolution 8 to abolish the class of supplementary units.
Web links
Individual evidence
- ↑ Le Système international d'unités . 9e édition, 2019 (the so-called "SI brochure", French and English).






























