Astronomical unit
| Physical unit | |
|---|---|
| Unit name | Astronomical unit |
| Unit symbol | |
| Physical quantity (s) | length |
| Formula symbol | |
| dimension | |
| system | Approved for use with the SI |
| In SI units |
(exactly) |
| Derived from | Earth's orbit radius |
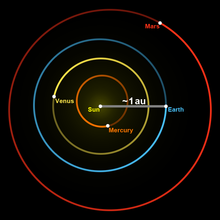
The astronomical unit (abbreviated AE, international au for English astronomical unit ) is a measure of length in astronomy : According to the definition , an AE measures exactly 149 597 870 700 meters . This is roughly the mean distance between the earth and the sun .
The astronomical unit, along with the light year and the parsec, is the most important unit among the astronomical units of measurement . It does not belong to the International System of Units (SI), but is approved for use with the SI. It is not a legal unit of measurement .
The astronomical unit was historically of great importance for astronomy, as most distance determinations, due to the methods used, provided the result directly in AU and not in meters. In the meantime, however, the conversion factor between AE and meters is known so precisely that the use of AE no longer offers any advantages in terms of accuracy. In 2012, the previous definition derived from the gravitational constant of the sun was abandoned and the AE was simply redefined as a certain number of meters. The AE has lost its original astrophysical meaning and is now just a conventional unit of length. Distances within the solar system are, however, still mostly given in AU, as this results in convenient numerical values.
The International Bureau of Weights and Measures has recommended the unit symbol au for astronomical units since 2014, as has the International Astronomical Union (IAU) . In contrast to this, the use of AE and AU has established itself in German-language literature.
Expressed in other interstellar length measures, the following size relation results for the astronomical unit:
1 AU = 499.004 784 light seconds = 1.581 250 74 10 −5 light years = 4.848 136 81 10 −6 parsec = 2π / (360 60 60) parsec = 149 597 870 700 meters .
definition
The AE was originally defined as the length of the major semi-axis of the earth's orbit , later as the radius of a circular orbit on which a hypothetical massless body orbited the sun in a given period of time (further details are explained in the history section ).
On August 30, 2012, the 28th General Assembly of the International Astronomical Union, meeting in Beijing, decided in "Resolution B2",
"... that the astronomical unit be re-defined to be a conventional unit of length equal to 149 597 870 700 m exactly, [...]" "... that the astronomical unit will be redefined as a conventional unit of length, which corresponds exactly to 149 597 870 700 m, [...]"
According to this redefinition, the AE is no longer a property of the solar system that can be determined by measurement, but is a distance with an exactly defined length in meters. The selected numerical value corresponds to the best measured value to date of 149 597 870 700 m ± 3 m.
The previous definition of the AE was based on the Gaussian gravitational constant , which, when expressed using the unit of length "1 AU", the time unit "1 day" and the unit of mass "1 solar mass", had a fixed numerical value by convention (see → Section definition from 1976 ). What numerical value the so defined unit of length "1 AU" assumed when it was to be expressed in SI units (ie in meters) had to be determined by observing the planetary movements. As a result of the redefinition, the length of the AE is now fixed in meters; the Gaussian gravitational constant is no longer required and will no longer be part of the astronomical constant systems in the future.
The numerical value of the heliocentric gravitational constant , expressed in astronomical units, was defined as a constant according to the previous definition. In the calculation of its numerical value in SI units, however, the current numerical value determined by observation for the length of the astronomical unit was included, so that a new measurement of the AE could result in a changed one. The direct determination of in SI units, which has become possible due to modern measurements, makes this detour via the AE superfluous. It is also conceivable that a possible change in time could move into the realm of measurability in the foreseeable future. According to the previous definition, this would have required the introduction of a time-varying AE, which is not necessary according to the new definition. More recent measurements (2011) already indicate a slight decrease in.
The accuracy of modern position measurements in the solar system is so high that relativistic corrections have to be taken into account. The transfer of the previous definition into a relativistic conceptual framework would have required additional conventions and resulted in a length of the AE that was dependent on the reference system. The newly defined AE, on the other hand, has the same length in all relativistic reference systems. The resolution explicitly states that the same definition should be used for all relativistic time scales (e.g. TCB , TDB , TCG , TT , etc.).
history
AE as a unit of length
The orbital times of the planets are easy to observe and were well known to early astronomers. With the help of Kepler's third law , the ratio of the orbital times of two planets could be inferred with practically the same accuracy about the ratio of their orbital radii. The ephemeris of that time could therefore calculate with high accuracy how many times z. B. Mars was further from the Sun than Earth at any given time. The major semiaxis of the earth's orbit was chosen as the measure of length, it was called “astronomical unit” and instead of the cumbersome expression “Mars is today 1.438 times as far from the sun as the major semiaxis of the earth’s orbit is long”, it was possible to simply say “Mars is today 1.438 AU away from the Sun ”. The distances expressed in this form as AE (actually the ratios of two distances to each other) could be determined quite precisely, in terrestrial lengths such as z. B. miles or meters, however, the distances were only known very imprecisely. For scientific purposes, the use of the AU as a unit of length was therefore an obvious choice, for which, however, it required a sufficiently precise definition.
First definition
According to Kepler's third law, the period of revolution of a planet of mass , which revolves around the sun (mass ) on an orbit with the major semiaxis, applies:
| (1) |
For two planets P1 and P2 it follows:
| (2) |
This law only contains relationships between the times of revolution, the masses and the major semi-axes. The Second Kepler's law similarly includes only a statement about the situation of the swept the driving beam at specific time intervals surfaces. These laws therefore initially supply the positions of the planets on an as yet undetermined scale. You can therefore choose the units of the lengths, time intervals and masses that occur in such a way that they make the calculations as simple as possible. In classical astronomy were chosen as commonly astronomical unit length , the length of the semimajor axis of the Earth's orbit (1 AE), as astronomical unit mass of the mass of the sun 1M ☉ and as astronomical unit time of the day 1 d.
Since the positions of the celestial bodies on the apparent celestial sphere (i.e. the angle of direction under which they appear to the observer) are independent of absolute scales, astronomers were able to carry out highly precise positional astronomy with these relative scales . The distance of a planet could also be specified for a desired point in time with high accuracy in astronomical units, the distance in meters, however, far less accurate, since the length of the astronomical unit in meters was only moderately known. Similarly, the masses of the planets could be given quite precisely in solar masses, much less precisely in kilograms.
Only in the last few decades has it been possible to measure distances with high accuracy (e.g. by means of laser distance measurement to the moon, by means of radar distance measurement to Mercury, Venus and Mars, or by measuring the signal transit times to space probes).
Gaussian constant of gravity
The numerical value of the gravitational constant in equation (1) depends on the choice of units for the occurring physical quantities. For the period of revolution of the planet it follows from that equation by rearranging:
| (3) |
With the abbreviations
| and | (4) |
surrendered:
| (5) |
CF Gauss in 1809 determined the value of the gravitational constant in astronomical units (semi-major axis of Earth's orbit as a unit of length AE, mean solar d as a unit of time, solar mass as a mass unit ) by the formula down to earth as a planet anwandte
| (6) |
| (7) |
and used the best numerical values for and at the time:
| (8th) | ( sidereal year ) |
| (9) |
| (10) |
This numerical value of the gravitational constant in astronomical units of measurement was subsequently used as the standard value for numerous astronomical calculations.
Definition from 1976
With constantly improved knowledge of and , the numerical value of could have been continuously improved. However, the Gaussian value soon formed the basis of numerous fundamental tables, which should have been recalculated with every change in . An alternative was in the equation
| (11) |
to keep the numerical value of and instead adjust the unit of length in which the measurement is made so that the new numerical value of measured in the new unit of length satisfies the equation for the new values of and again (an example follows in the next section). The semi-major axis of the earth's orbit thus lost its defining status: in astronomical units, it no longer had a strict length of 1 AU. The unit of length with respect to which the numerical value satisfying the equation was assumed was the new AE. The definition from 1976 was:
“The astronomical unit of length is the length (A) for which the Gaussian gravitational constant ( ) assumes the value 0.017 202 098 95, if the units of measurement are the astronomical units of length, mass and time. [...] "
Since the definition of the AE was no longer given by the earth's orbit anyway, the astronomers broke away from the earth's mass and referred the new definition to a fictitious body with negligibly small mass:
| (12) |
If one imagines such a fictitious body on an undisturbed path, which obeys law (1) and whose major semi-axis is equal to the new unit of length to be determined
| (13) |
so applies to him
| (14) |
This defining body has a period of rotation of
| Days | (15) | (so-called Gaussian year ) |
The fictitious orbit can be assumed to be circular without loss of general validity. The definition of AE can therefore be formulated synonymously as
The astronomical unit AE is the radius of a circular orbit, on which a body with negligible mass and free of disturbances orbits a central star in days, whereby the Gaussian gravitational constant is.
The practice of recording the numerical value of and using it to define the AE was unofficially common since the 19th century. It was officially adopted by the IAU in 1938, when it laid down the Gaussian numerical value for by resolution at the 6th General Assembly . In 1976, at the 28th General Assembly, an explicit textual definition was given for the first time.
Earth orbit and AE
For the periods of revolution of the earth and the defining fictitious body , the Third Kepler Law (2) provides :
| (21) |
Resolve for and insert the current numerical values
| (22) |
and
| (23) |
results
| (24) |
The ratio of their major semiaxes (21) follows from the ratio of the orbital times of the two bodies . But one of them precisely defines the astronomical unit; the result is the major semiaxis of the earth's orbit, expressed in AU, which is now slightly larger than 1 AU.
If you insert these new numerical values for , and instead of the old Gaussian values in the Gaussian formula (10) , you still get the Gaussian numerical value for . If the given numerical value is added to the orbital period measured in days and the stated numerical value to the earth mass measured in solar masses , then the requirements of the IAU definition are met if the major semi-axis of the earth's orbit measured in AE receives the numerical value 1,000 000 036. The unit of length in which the semi-major axis must be measured in order to assume this numerical value is the current AE that is compatible with the current values of and . If it is possible to determine the length of the major semi-axis in meters, the length of the AE in meters is known from this relationship.
Heliocentric gravitational constant
If you convert the period of revolution and the major semi-axis of the fictitious massless body from astronomical units of measurement back to SI units
| , | (31) |
| (32) |
and if the result is inserted into equation (1) , we get:
| (33) |
where the conversion factor to be determined is from astronomical units to meters. Insertion of
| (34) |
and solve for yields:
| (35) |
(The heliocentric gravitational constant is the product of the Newtonian gravitational constant and the solar mass . It can be derived from the measurement of the planetary orbits and is known with much greater accuracy than its two individual factors.)
The formula just mentioned represents nothing other than the conversion of k 2 (in astronomical units) to or (in SI units). In astronomical units of measurement always has the same numerical value determined by the definition of the AE. In SI units, the numerical value of depends on the current numerical value determined by observation for the length of the astronomical unit.
The 1976 definition does not provide for a possible physically real variability of , for example, a cosmological variability of or the loss of mass of the sun. Should it become necessary to describe a time-varying AE due to increased measurement accuracy , this could only happen through the very unsatisfactory use of a time-varying AE (since according to the definition it is fixed on its given numerical value).
The redefinition of the AE from 2012 decouples GM ☉ and AE and thus opens the way to the direct measurement of (and its possible variability) in SI units. The detour via the AE is no longer necessary. A change in the numerical value of the AE as a result of a new determination does not result in a change in the numerical value of any more.
Measurement
In order to determine the length of the AE in meters, it was necessary to measure the known distances in AE to the planets or the sun in meters. Until about the middle of the 20th century, this could only be done by triangulation using optical means. The AE was mainly derived from highly precise angle measurements ( parallaxes ), which were carried out from observatories as far apart as possible to the planets Venus and Mars as well as to asteroids close to the earth . A brief overview of these provisions of the AE up to the early 20th century can be found in the → article Venus transit .
For several decades, distances in the solar system can be measured directly. The modern value of the AE was determined by means of radar and other distance measurements from the earth to the neighboring planets and to space probes. From the measurement of the "mean movements" (ie the mean speeds) or the orbital periods of the planets, which can be determined very precisely, the major semiaxes of the planets follow with the same accuracy via the third Kepler law (in the Newtonian version including relativistic corrections) AE. The distance measurements to the planets by means of radar determine their orbital geometry and thus the major semiaxes of their orbits in meters; the ratio to the length of the major semi-axes in AU provides the length of the AU in meters and the numerical value of in .
The following table lists, among other things, some modern ephemeris that were obtained by adapting the physical equations of motion to extensive observation material. Each such adjustment provides, among other things, as just described a numerical value for the scale factor of the solar system, which indicates the length of the AE in meters (the uncertainties mentioned are usually formal uncertainties that are estimated in the course of the adjustment from the consistency of the measurement data with each other and which are usually too optimistic. A more realistic picture of the uncertainties can be obtained by comparing the results with one another):
| AE (in m) | Source or ephemeris |
|---|---|
| 149 597 850,000 ± 400,000 | Radar to Venus, Pettengill 1962 |
| 149 598 845 000 ± 250 000 | Radar to Venus, Muhleman 1962 |
| 149 597 870 000 ± 2 000 | IAU (1976) - System of Astronomical Constants |
| 149 597 870 684 ± 30 | JPL DE102, Newhall 1983 |
| 149 597 870 660 ± 2 | JPL DE118, DE200, Standish 1990 |
| 149 597 870 620 ± 180 | Krasinsky 1993 |
| 149 597 870 691 ± 6 | JPL DE405, Standish 1998 |
| 149 597 870 691.2 ± 0.2 | IAA EPM2000, Pitjeva 2000 |
| 149 597 870 697.4 ± 0.3 | JPL DE410, Standish 2003 |
| 149 597 870 696.0 ± 0.1 | IAA EPM2004, Pitjeva 2004 |
| 149 597 870 700.85 ... | JPL DE414, Standish 2006 |
| 149 597 870 700 ± 3 | Average; Pitjeva and Standish 2009 |
The JPL's DE405 ephemeris is currently the basis for numerous yearbooks and other ephemeris works. The numerical value derived from it of 149 597 870 691 m for the AE was therefore the most common standard value for several years. He was recommended by the IERS .
Strictly speaking, the numerical value mentioned is not the SI value, since the calculations of the planetary movements are based on the time scale TDB, which relates to the center of gravity of the solar system , while the SI second, by definition, relates to the earth's surface (more precisely: the geoid ) and is based on relativistic Establishing runs a little faster. If you convert the TDB value to strict SI units, the result is:
| AE (in m) | Time scale |
|---|---|
| 149 597 870 691 | TDB |
| 149 597 871 464 | SI |
The 27th General Assembly of the International Astronomical Union decided in 2009 to recommend the mean value of 149 597 870 700 m ± 3 m derived from the best measurements at that time for general use within the framework of the "IAU 2009 System of Astronomical Constants".
The 28th General Assembly of the International Astronomical Union decided in 2012 to depart from the previous definition (according to which the length of the astronomical unit in meters was always the result of a measurement ) and the astronomical unit simply as a distance of length 149 597 870 700 m (exactly) to be redefined.
Variability of the Gaussian AE
The AE, which was redefined in 2012, is set by a fixed numerical value and is therefore unchangeable by definition. The earlier AE defined by the Gaussian constant, however, is a scale factor of the solar system to be determined by measurement, which possibly reflects changes in the solar system. Measurements to determine the AE in the earlier sense can therefore still be useful for uncovering such possible changes.
Evaluations of radar measurements seem to indicate that the scale factor of the solar system is slowly increasing. Rates of change of 15 ± 4 meters / century, 7 ± 2 meters / century and 1.2 ± 1.1 meters / century are given; the cause is so far unknown.
- The obvious assumption that the observed effect is caused by the expansion of the universe turns out to be incorrect. Theoretical studies using common cosmological models show that the cosmic expansion has no measurable effects on the movement of the planets.
- The mass loss of the sun caused by the solar wind and energy radiation leads to a long-term enlargement of the planetary orbit radii by about 0.3 meters / century. Due to the decrease in the gravitational force exerted by the sun, this effect causes an increase in the distances between the planets from the sun and one another, but due to the decrease in the solar mass M ☉ , at the same time, due to equation (34), a decrease in the AE defined by the Gaussian constant.
- A decrease in the gravitational constant by about 2 · 10 −10 percent per year could explain the effect, however, according to more recent measurements, a possible variability of G cannot be greater than about 0.06 · 10 −10 percent per year.
So far it cannot be ruled out that it is merely a matter of systematic errors in the observations. Effects that have not been taken into account when calculating the planetary orbits or the signal propagation are considered less likely. Attempts at explanations in the context of more exotic gravitation theories such as string theory are currently viewed as "highly speculative".
literature
- E. Myles Standish : The Astronomical Unit now. Proceedings IAU Colloquium No. 196, 2004, pp. 163-179 ( online , PDF, 1.5 MB).
Individual evidence
- ↑ The International System of Units (SI) . German translation of the BIPM brochure "Le Système international d'unités / The International System of Units (8e édition, 2006)". In: PTB-Mitteilungen . tape 117 , no. 2 , 2007 ( Online [PDF; 1.4 MB ]).
- ↑ It is not mentioned in EU Directive 80/181 / EEC , nor in the Swiss Federal Metrology Act .
- ^ The International System of Units. supplement 2014. In: bipm.org. 2014; P. 13 (PDF; 628 kB).
- ↑ a b c d IAU: Resolutions B1, B2, B3 and B4. Adopted at the General Assembly 2012 (PDF; 122 kB).
- ^ A b The astronomical unit gets fixed. In: nature.com.
- ^ A b IAU: Numerical Standards for Fundamental Astronomy - IAU 2009 System of Astronomical Constants. Retrieved January 8, 2019.
- ↑ a b N. Capitaine, B. Guinot, SA Klioner: Proposal for the Re-definition of the Astronomical Unit of Length Through a Fixed Relation the the SI Meter. In: N. Capitaine (Ed.): Proceedings of the Journées 2010 “Systèmes de Référence Spatio-Temporels”. Observatoire de Paris, 2011, ISBN 978-2-901057-67-3 , pp. 20-23 ( PDF; 233 kB ).
- ↑ EV Pitjeva, NP Pitjev: Estimations of changes of the Sun's mass and the gravitational constant from the modern observations of planets and spacecraft. In: Solar System Research. 2011 ( arxiv : 1108.0246 ):
- ↑ A. Schödlbauer: Geodetic Astronomy. Walter de Gruyter, Berlin 2000, ISBN 3-11-015148-0 , p. 76.
- ^ CF Gauß: Theoria motus corporum coelestium in sectionibus conicis solem ambientium. Perthes, Hamburg 1809, p. 14 ( digitized version ).
- ↑ A. Schödlbauer: Geodetic Astronomy. Walter de Gruyter, Berlin 2000, ISBN 3-11-015148-0 , p. 113.
- ^ IAU: Resolutions of the XVIth General Assembly, Grenoble, France, 1976. ( PDF; 1.1 MB ): “The astronomical unit of length is that length (A) for which the Gaussian gravitational constant (k) takes the value 0.017 202 098 95 when the units of measurement are the astronomical units of length, mass and time. [...] "
- ↑ A. Schödlbauer: Geodetic Astronomy. Walter de Gruyter, Berlin 2000, ISBN 3-11-015148-0 , p. 111.
- ↑ PK Seidelmann (Ed.): Explanatory Supplement to the Astronomical Almanac. In: University Science Books. Mill Valley 1992, ISBN 0-935702-68-7 , p. 722: "[T] he radius of a circular orbit in which a body of negligible mass, and free of perturbations, would revolve around the Sun in 2π / k days , where k is the Gaussian gravitational constant. "
- ↑ IAU: VIth General Assembly - Stockholm, Sweden - 1938. Adopted at the General Assembly in 1938 (PDF 1.22 MB).
- ^ The Astronomical Almanac for the Year 2006. United States Government Printing Office, Washington 2004, ISBN 0-11-887333-4 ; S. K7 (sum of the masses of the earth and moon).
- ^ The Astronomical Almanac for the Year 2006. United States Government Printing Office, Washington 2004, ISBN 0-11-887333-4 ; S. C1.
- ↑ A. Schödlbauer: Geodetic Astronomy. Walter de Gruyter, Berlin 2000, ISBN 3-11-015148-0 , p. 112.
- ↑ XX Newhall, EM Standish , JG Williams: DE 102: a numerically integrated ephemeris of the Moon and planets spanning forty-four centuries. In: Astronomy and Astrophysics. 125, 150-167 (1983) ( bibcode : 1983A & A ... 125..150N ).
- ↑ XX Newhall, EM Standish, JG Williams: DE 102: a numerically integrated ephemeris of the Moon and planets spanning forty-four centuries. In: Astronomy and Astrophysics. 125, 150-167 (1983) ( bibcode : 1983A & A ... 125..150N ), p. 162.
- ^ GH Pettengill, HW Briscoe, JV Evans, E. Gehrel, GM Hyde, LG Kraft, R. Price, WB Smith: A Radar Investigation of Venus. In: Astronomical Journal. Vol. 67 (1962), pp. 181-190 ( bibcode : 1962AJ ..... 67..181P ).
- ^ DO Muhleman, DB Holdridge, N. Block: The Astronomical Unit Determined by Radar Reflections from Venus. In: Astronomical Journal. Vol. 67 (1962), pp. 191-203 ( bibcode : 1962AJ ..... 67..191M ).
- ↑ T. Lederle: The IAU (1976) system of astronomical constants. In: Communications from the Astronomical Society . No. 48 (1980), pp. 59-65 ( bibcode : 1980MitAG..48 ... 59L ).
- ↑ XX Newhall, EM Standish, JG Williams: DE 102: a numerically integrated ephemeris of the Moon and planets spanning forty-four centuries. In: Astronomy and Astrophysics. 125, 150-167 (1983) ( bibcode : 1983A & A ... 125..150N ), AE p. 160, uncertainty p. 150, p. 162.
- ^ EM Standish: The observational basis for JPL's DE 200, the planetary ephemerides of the Astronomical Almanac. In: Astronomy and Astrophysics. 233, 252-271 (1990) ( bibcode : 1990A & A ... 233..252S ).
- ↑ PK Seidelmann (Ed.): Explanatory Supplement to the Astronomical Almanac. In: University Science Books. Mill Valley 1992, ISBN 0-935702-68-7 , p. 302.
- ^ GA Krasinsky et al: The Motion of Major Planets from Observations 1769–1988 and Some Astronomical Constants. In: Celestial Mechanics and Dynamical Astronomy. 55, 1-23 (1993) ( bibcode : 1993CeMDA..55 .... 1K ).
- ↑ JPL Interoffice Memorandum IOM 312.F-98-048; August 26, 1998 ( online , PDF; 928 kB); Uncertainty according to Astronomical Almanac 2006, p. K6.
- ↑ EV Pitjeva: Progress in the determination of some astronomical constants from radiometric observations of planets and spacecraft. In: Astronomy and Astrophysics. 371, 760-765 (2001) ( online, PDF; 108 kB).
- ↑ JPL Interoffice Memorandum IOM 312.N - 03 - 009; April 24, 2003 ( online , PDF; 6.7 MB).
- ↑ a b E. V. Pitjeva: Precise determination of the motion of planets and some astronomical constants from modern observations. In: Proceedings IAU Colloquium. No. 196, 2004, pp. 230–241 ( online, PDF; 190 kB).
- ↑ JPL Interoffice Memorandum IOM 343R - 06 - 002; April 21, 2006 ( online , PDF; 1.0 MB).
- ↑ a b E. V. Pitjeva, EM Standish: Proposals for the masses of the three large largest asteroids, the Moon-Earth mass ratio and the Astronomical Unit. In: Celestial Mechanics and Dynamical Astronomy. Volume 103, Issue 4 (April 2009), pp. 365-372, doi: 10.1007 / s10569-009-9203-8 .
- ^ DD McCarthy, G. Petit (Ed.): IERS Conventions (2003). Publishing house of the Federal Agency for Cartography and Geodesy, Frankfurt / M. 2004 ( online ).
- ^ The Astronomical Almanac for the Year 2006. United States Government Printing Office, Washington 2004, ISBN 0-11-887333-4 ; S. K6.
- ↑ B. Luzum et al .: The IAU 2009 system of astronomical constants: the report of the IAU working group on numerical standards for Fundamental Astronomy. In: Celestial Mechanics and Dynamical Astronomy. Vol. 110, Issue 4 (August 2011), pp. 293-304 doi: 10.1007 / s10569-011-9352-4 .
- ↑ a b c d e G. A. Krasinsky, VA Brumberg: Secular Increase of Astronomical Unit from Analysis of the Major Planet Motions, and its Interpretation. In: Celestial Mechanics and Dynamical Astronomy. 90: 267-288 (2004) doi: 10.1007 / s10569-004-0633-z .
- ^ A b E. M. Standish: The Astronomical Unit now. In: DW Kurtz (Ed.): Transits of Venus: New Views of the Solar System and Galaxy. In: Proceedings IAU Colloquium. No. 196, 2004, 163–179 ( online , PDF; 1.5 MB).
- ↑ a b E. V. Pitjeva, NP Pitjev: Estimations of changes of the Sun's mass and the gravitational constant from the modern observations of planets and spacecraft. In: Solar System Research. 2011 ( arxiv : 1108.0246 ):
- ↑ U. Bastian: The sidereal year and the astronomical unit. In: Stars and Space. 6/2007, p. 9.
- ↑ O. Preuss, H. Dittus, C. Lämmerzahl: Surprises on the doorstep - Is the physics within the solar system really understood? Stars and Space 4/2007, 27–34.





































![{\ displaystyle a _ {\ mathrm {E}} = {\ sqrt [{3}] {{\ frac {U _ {\ mathrm {E}} ^ {2}} {(2 \ pi / k) ^ {2} }} \ cdot (1+ \ mu _ {\ mathrm {E}})}} = 1 {,} 000 \, 000 \, 036 \, \ mathrm {AE}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc805dc6961163fb572c73ea6a885732ab802807)









