Earth orbit

Earth orbit
Mean elliptical orbital elements , related to the mean ecliptic and the mean equinox for epoch J2000.0
Major semi-axis	1,000 001 017 8  AE 149 598 022.96 km
Numerical eccentricity	0.016 708 634 2
Tilt towards the ecliptic	0 °
Ecliptical length of the perihelion	102.937 348 08 °
Mean ecliptical longitude of the earth at time J2000.0	100.466 456 83 °
Medium sidereal movement	0.985 609 112 5 ° / day Period: 365.256 363 2 days
Medium tropical movement	0.985 647 358 ° / day Period: 365.242 190 4 days

The Earth's orbit is the orbit (or revolution) of the earth around the sun . It is thus the path that the earth describes in its annual orbit around the sun.

Path geometry

shape

True-to-scale representation of the earth's elliptical orbit (orange) compared to a circle (gray).

The earth's orbit is described as a good approximation by an ellipse ( Kepler's orbit ) with the sun in one of the two focal points , as required by Kepler's first law .

With a numerical eccentricity of 0.0167, this ellipse deviates only very little from a circular path. To the naked eye, the difference between such a circle-like ellipse and a circle cannot be determined; it appears like a circle that has been slightly shifted from the center. The point closest to the sun is the perihelion , the point furthest from the sun is the aphelion . ${\displaystyle \varepsilon }$

The semi-major axis a of the earth's orbit is 149.598 million kilometers (one astronomical unit , AU). This is also the mean distance between the earth and the sun if the mean value is calculated evenly along the path. In perihelion, the earth is 147.09 million kilometers from the sun, while in aphelion it is 152.10 million kilometers. These two extreme values ​​only deviate from the mean by 1.67%.

On average over time , the distance between the earth and the sun is slightly more than one AU (namely 1,00014 AU), as the earth stays a little longer away from the sun than near the sun due to its uneven orbital speed.

The earth moves in a right-hand direction on its orbit, i.e. counterclockwise when viewed from the North Star. The average rail speed is 29.7859 km / s (107,229 km / h). It fluctuates between 30.29 km / s in perihelion and 29.29 km / s in aphelion.

The speed of the earth during its orbit leads to the aberration of the starlight observed. Their different positions on the orbit during an orbit lead to parallax in the observed star positions and to variations of up to ± 8.3 minutes in the light transit times between the object under observation and the earth.

The length of the earth's orbit is around 940 million km. The earth moves about 2.57 million km on its orbit per day, that is about 202 earth diameters . In one second the distance from earth to sun covers an area of ​​over 2 billion km²; this value is constant according to Kepler's second law (the “area law”).

Since the earth has a massive moon, its center on the Kepler ellipse does not revolve around the sun, as is the case with moonless planets , but the common center of gravity of the moon and earth (the barycenter of the earth-moon system). This center of gravity is still in the interior of the earth - at a depth of approx. 1700 km - but on average about 4670 km from the center of the earth. The center of the earth itself circles around the center of gravity and consequently follows a serpentine line along the elliptical path, with one oscillation per month. When the "earth orbit" is spoken of, the uniform elliptical orbit of the center of gravity is usually meant, not the undulating orbit of the earth itself. When specifying the times at which certain orbit points are passed (e.g. the vernal equinox or the perihelion) , a distinction must be made as to whether the information refers to the earth-moon center of gravity or to the center of the earth. See also the sections → Position of the vestibules and → Disturbances in length .

location

Position of the plane

The ecliptic (large red circle) is the orbit of the earth projected onto the celestial sphere (small red circle). The celestial equator (turquoise) is the earth's equator projected onto the celestial sphere.

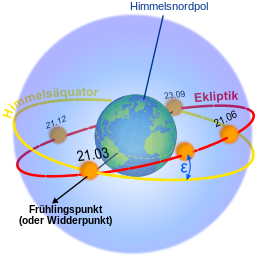
As always when a celestial body moves through its orbit under the influence of a central force , the orbit of the earth-moon center of gravity also lies in one plane. There are no sideways forces that could bend the track perpendicular to the plane of the track. This orbital plane is also called the ecliptic plane or ecliptic for short and serves, among other things, as a reference plane for astronomical coordinates .

If one imagines the plane of the orbit to be continued infinitely in all directions, then its line of intersection with the apparent celestial sphere results in a great circle around the sky, which is also called the ecliptic. Viewed from the center of the sun , the earth moves along this ecliptic line around the fixed star sky once a year. Seen from the earth, it is the sun that moves along the ecliptic during its annual migration through the fixed stars. For more details, see the section → Sun path and the article → Sun position . The position of the earth as seen from the sun and the position of the sun as seen from the earth are always opposite each other on the celestial sphere. The characteristics of the earth's and (apparent) solar orbit are the same, and both perspectives can be used, but they must not be confused with one another. At the beginning of spring, for example, the sun as seen from the earth is by definition at the point of spring , while at the same time the earth as seen from the sun is at the opposite autumn point.

The position of the ecliptic plane in space can be described particularly easily with the help of the poles of the ecliptic. These are those points at which a straight line perpendicular to the plane of the ecliptic penetrates the celestial sphere. These two opposite points on the celestial sphere are each 90 ° away from all points of the ecliptic great circle. The position and course of the ecliptic are completely determined when one of its poles is given. At time J2000.0 - January 1, 2000 12:00 TT - the poles of the ecliptic were on the coordinates

North Ecliptic Pole:	RA :	18 h 0 m 0.0 s (exact),	Dek :	+ 66 ° 33 ′ 38.588 ″	(a point in the constellation Dragon )
South Ecliptic Pole:	RA:	6 h 0 m 0.0 s (exact),	Dek:	−66 ° 33 ′ 38.588 ″	(a point in the constellation swordfish )

With the help of the poles it is also easy to determine the angle of intersection of two intersecting planes - it is simply the angular distance between the associated poles. For the north pole of the galactic plane, for example, at time J2000.0:

Northern Galactic Pole:

RA: 12 h 51 m 26.2755 s ,

Dec: + 27 ° 7 '41.704 "

(a point in the constellation Haar der Berenike )

The great circle distance between the northern ecliptical and the northern galactic pole is 60.2 °, so the earth's orbit plane is also inclined to the galactic plane by this angle.

Ecliptic and Celestial Equator

The axis of rotation of the earth is not perpendicular to the plane of the orbit , but is slightly inclined. Correspondingly, the equatorial plane of the earth or its projection onto the apparent celestial sphere, the celestial equator , does not lie in the plane of the orbit . The angle between the ecliptic plane and the equatorial plane, the so-called skew of the ecliptic, is currently about ε = 23.44 °. The line of intersection between the two planes marks a common reference line both on the ecliptic and on the equator. The sun is in one of the two directions defined by the reference line at the beginning of spring when the sun, moving on the ecliptic (from the point of view of the earth), crosses the celestial equator and passes through the intersection of the ecliptic and equator. The direction to this " spring point " is used as the zero point for astronomical coordinate systems. Currently this direction points to a point in the Pisces constellation .

The right ascension is counted right along the celestial equator starting from the vernal equator, the declination perpendicular to it. The ecliptic length counted from vernal equinox starting rechtläufig along the ecliptic, the ecliptic width perpendicular thereto. During a 365-day orbit orbit, the ecliptical length of the earth changes by 360 degrees, so it covers an average of just under a degree per day.

Position of the apses

The apsidal line - the connecting line between perihelion and aphelion - describes the orientation of the earth's orbit ellipse within the orbit plane. The perihelion had the ecliptical longitude 102.9 ° at the time J2000.0 and therefore currently points to a point in the constellation Gemini . The earth-moon center of gravity currently passes through perihelion on January 3rd or 4th and aphelion on July 4th or 5th.

The center of the earth, on the other hand, runs along the wavy line caused by the moon, which has its own perihelion because of the wavy orbit shape that differs slightly from the regular ellipse. This perihelion at the center of the earth lies from year to year - depending on the current position of the moon - at a slightly different point on the orbit. The center of the earth therefore passes its own perihelion at significantly more irregular intervals, usually between January 2nd and 5th. Details are explained in the article → Apse (astronomy) .

Railway disruptions

The gravitational influences of the other planets exert disturbances on the earth's orbit, which change their shape and position slightly but continuously.

Numerical eccentricity

Long-term behavior of the eccentricity of the earth's orbit over two million years.

The numerical eccentricity of the earth's orbit is currently around 0.0167 and is slowly decreasing. For the period between about 4000 BC BC and AD 8000, the course of the eccentricity over time is described to a good approximation by the polynomial

${\displaystyle {\begin{alignedat}{4}\varepsilon \,=&&\,0{,}016\,708\,6342&&\,-&\,0{,}000\,420\,3654&&\cdot t\\&\,-&\,0{,}000\,012\,6734&\cdot t^{2}&\,+&\,0{,}000\,000\,1444&&\cdot t^{3}\\&\,-&\,0{,}000\,000\,0002&\cdot t^{4}&\,+&\,0{,}000\,000\,0003&&\cdot t^{5}\\\end{alignedat}}}$

Here is the TDB measured in Julian millennia from the standard epoch J2000 . So for the Julian day number is ${\displaystyle t}$ ${\displaystyle JD}$

${\displaystyle t={\frac {JD-2451545{,}0}{365250}}}$.

The polynomial does not provide any meaningful values for values ​​far outside the range . ${\displaystyle -6<t<6}$

Considered over longer periods of time (see adjacent diagram), the num. Assume eccentricity values ​​between just under 0.06 and almost zero. It reaches the next minimum with 0.0023 around the year 29500, an even lower minimum with 0.0006 around the year 465000. The earth's orbit will then temporarily be practically circular.

How much solar radiation the earth receives on average during a year depends on the eccentricity of the earth's orbit. If the earth receives the irradiance S _a at a distance a (major semi-axis) from the sun on a surface perpendicular to the sun, it receives the radiation power at a distance r on its cross-sectional area A.

${\displaystyle W\,=\,S_{a}\left({\frac {a}{r}}\right)^{2}\cdot A}$

The annual energy input received during a year of length T results from integration over time:

${\displaystyle W_{T}\,=\,\int _{0}^{T}Wdt\,=\,S_{a}A\int _{0}^{T}\left({\frac {a}{r}}\right)^{2}dt\,=\,{\frac {S_{a}AT}{\sqrt {1-\varepsilon ^{2}}}}}$

The annual energy input depends not only on S _a but also on the numerical eccentricity : It increases (while S _a remains the same ) when the eccentricity increases. Because of its lower speed in the vicinity of the apple, the earth spends an above-average length of time in the half of the orbit far from the sun. As the eccentricity increases, this part of the orbit moves further away from the sun. This irradiation loss, which increases with the eccentricity, is more than compensated for by the quadratic increase in irradiance in the perihelion, which is increasingly closer to the sun. The long-term variation in the annual energy input caused by the variability of the eccentricity is only a fraction of a percent, but it can still be climatologically relevant. ${\displaystyle \varepsilon }$

The main period of fluctuations in eccentricity is around 100,000 years (see also → Milanković cycles ).

The irradiance S ₀ , averaged over the year, is the solar constant . It is

${\displaystyle S_{0}\,:=\,{\frac {W_{T}}{A\cdot T}}\,=\,{\frac {S_{a}}{\sqrt {1-\varepsilon ^{2}}}}}$

Strictly speaking, the solar constant is therefore not identical to the irradiance S _a at the “mean distance” a . However, the deviation is only about 0.1 percent.

Perihelion

Schematic and greatly exaggerated representation of the perihelion rotation (blue dots: perihelion, dotted lines: ellipse axis).

The axis of the ellipse rotates slowly in the plane of the orbit, namely in the same direction in which the earth traverses the orbit (right-hand). As a result of this so-called perihelion rotation , the perihelion moves once around the sun in about 110,000 years with respect to the fixed star background. For the period between about 4000 BC BC and 8000 AD, the mean ecliptical length of the perihelion is described to a good approximation by the polynomial

${\displaystyle {\begin{alignedat}{4}\varpi \,=&&\,102{,}937\,348\,08^{\circ }&&\,+&\,3{,}225\,653\,583^{\circ }&&\cdot t\\&\,+&\,0{,}014\,798\,825^{\circ }&\cdot t^{2}&\,+&\,0{,}000\,039\,153^{\circ }&&\cdot t^{3}\\&\,-&\,0{,}000\,031\,778^{\circ }&\cdot t^{4}&\,+&\,0{,}000\,001\,328^{\circ }&&\cdot t^{5}\\\end{alignedat}}}$

where has the same meaning as in the formula for the eccentricity. The resulting angle relates to the mean ecliptic and the (fixed) mean vernal equinox for epoch J2000.0. If one relates the mean length of the perihelion instead to the current mean spring point, which migrates backwards towards it (see section → Seasons ), it changes correspondingly faster: ${\displaystyle t}$

${\displaystyle {\begin{alignedat}{4}\varpi '\,=&&\,102{,}937\,348\,08^{\circ }&&\,+&\,17{,}194\,598\,028^{\circ }&&\cdot t\\&\,+&\,0{,}045\,688\,325^{\circ }&\cdot t^{2}&\,-&\,0{,}000\,017\,680^{\circ }&&\cdot t^{3}\\&\,-&\,0{,}000\,033\,583^{\circ }&\cdot t^{4}&\,+&\,0{,}000\,000\,828^{\circ }&&\cdot t^{5}\\&\,+&\,0{,}000\,000\,056^{\circ }&\cdot t^{6}&&&&\\\end{alignedat}}}$

With regard to this "spring equinox of the date", the perihelion completes a orbit in about 21,000 years. Since the calendar is linked to the position of the sun in relation to the vernal equinox, the point in time of the passage of perihelion also runs through the calendar with this period: Around the year 1600 the passage of perihelion fell between December 26th and 28th; around the year 2500 it will fall on January 10-13.

How the total solar radiation available during the year is distributed over the seasons depends on the mutual position of perihelion and vernal equinox. When a season coincides with the passage of the perihelion (currently the northern hemisphere winter), it receives somewhat more radiation from the sun due to the distance than if it coincides with the passage of the apple 10,500 years later. At the same time, because of the greater orbital speed of the earth, it is also the shortest time of year (compare the explanations in the article → Season )

The precession of the perihelion related to the spring equinox of the date influences the development of the individual seasons. It is therefore also called "climatic precession".

Slope and knot line

Ecliptic for reference

Long-term behavior of the inclination of the earth's orbit with respect to the ecliptic of 1850, plotted over two million years.

The earth's orbit plane slowly changes its position in space due to the disturbances. Usually this plane itself is used as a reference for orbital inclinations in the solar system, but the current inclination of the earth's orbit plane, related to the current earth orbit plane (i.e. to itself), would always be zero. Instead, the inclination can sensibly be specified with reference to a fixed earth orbit, namely the earth's orbit at a certain, suitably selected time.

The current earth orbit intersects the earth's orbit as it was at time J2000.0 along a straight line of intersection (the “ nodal line ”), which is directed in the direction of the ecliptical longitude 174.8 °. It rotates slowly around this line of intersection at a rate of 47 arcseconds per century, while the line of intersection itself travels at a speed of −0.241 degrees per century along the fixed earth orbit plane.

The diagram opposite shows the temporally variable inclination of the earth's orbit with respect to the earth's orbit of 1850. This inclination reached its last maximum of 4 ° 00 'around the year 38300 BC. And will reach its next maximum of 2 ° 23 'around the year 34100 AD.

In 1850 the earth's orbit coincided with the earth's orbit of 1850 (by definition), so that the inclination briefly assumed the value zero. A similar coincidence of the migratory plain with the 1850 reference level occurred around the year 628,000 BC. To observe.

Invariable plane for reference

Another possible reference plane is the “invariable plane” of the solar system, that is, the plane that is perpendicular to the total angular momentum vector of the solar system. The angular momentum is a conserved quantity, the total angular momentum of the solar system can only be changed by the action of an external torque . The gravitational field of the galaxy only exerts a negligible torque on the solar system, so the orientation of the total angular momentum vector and thus the orientation of the plane perpendicular to it can be regarded as practically constant. The following applies to this alignment:

Northern pole of the invariable plane: RA (J2000,0) = 273.8527 °, Dec. (J2000,0) = 66.9911 ° (one point in the constellation Dragon).

The pole of the ecliptic precesses around the pole of the invariable plane under the influence of the disturbances. In the period from 500,000 years ago to 500,000 years after 2000, the ecliptic pole orbits the invariable pole fourteen times, with the distance between the two poles (i.e. the inclination of the two planes to one another) fluctuating between almost zero and just under 3 degrees. At time J2000.0, the ecliptic and the invariable plane were inclined to one another by 1.5787 °, the ecliptical length of the ascending node of the invariable plane on the ecliptic was 107.5822 °.

Precession

The movement of the ecliptic plane described by the temporal variability of inclination and nodal line is called “planetary precession”, more recently also called “precession of the ecliptic”. If the celestial equator were immobile, the precession of the ecliptic alone would lead to a migration of the vernal equinox of about 12 ″ per century and a decrease in ecliptic skew of about 47 ″ per century. However, due to the action of the sun and moon on the earth's body, the equator also moves ("lunisolar precession", recently also referred to as "precession of the equator"). The resulting movement of the vernal equinox as the intersection of the ecliptic and the equator is the “ general precession ”. It's a good 5000 ″ per century, which is largely due to the movement of the equator.

Disturbances in length

The gravitational effect of the other planets not only leads to changes in the shape and position of the earth's orbit, it can also influence the position of the earth-moon system on the orbit by slightly accelerating or delaying its movement.

The change in the ecliptical length of the Earth-Moon system caused by Venus compared to the undisturbed mean value, however, always remains smaller than 12 arc seconds (″), that caused by Mars smaller than 5 ", that by Jupiter under 13" and that by Saturn under 1 ″. The influence of the other planets is even less. The disturbance in ecliptical length is therefore always less than about 31 ″. The earth-moon system covers this distance at a speed of around one degree per day in just under a quarter of an hour. The point in time at which the earth-moon system passes through a certain orbit point (e.g. the vernal equinox) can deviate by this amount of time from the mean, undisturbed point in time due to the disturbances.

The fact that it is actually the center of gravity of the earth-moon system, which follows the Kepler orbit, while the earth in turn orbits this center of gravity, can be understood as an orbital disruption of the earth caused by the presence of the moon. The distance between the center of the earth and the earth-moon center of gravity is (with the greatest possible distance between earth and moon ) about 4942 km. The center of the earth can run ahead or behind the steadily moving center of gravity by this distance. At a rail speed of around 30 km / s, it takes just under three minutes to cover that distance. The points in time at which the center of the earth or the earth-moon center of gravity pass through a certain orbit (e.g. the vernal equinox) can therefore differ by this amount of time.

The times at which the center of the earth passes through the perihelion or aphelion, however, as already mentioned, can deviate from the mean value by several days. Responsible for this is not a disturbance in ecliptical length, but the wave movement of the center of the earth around the earth-moon center of gravity. Depending on the phase of the moon near the apse, it can carry the center of the earth at significantly different orbital points in the maximum proximity or distance to the sun. For details see the article → Apse

Major semi-axis

In contrast to the other orbit elements, the major semi-axis of the earth's orbit shows only minor fluctuations and no long-term drift. A long-term calculation of the planetary orbits over 250 million years in the past and in the future only shows fluctuations in the major semi-axis between about 0.99997 and 1.00003 astronomical units, with the mean value remaining constant.

Period of circulation

The period of revolution (or period of revolution) of the earth around the sun is called one year . The earth needs about 365¼ days for one orbit, as can be seen from the third Kepler's law for an undisturbed elliptical orbit with the help of the law of gravitation (for the meaning of the symbols see the article → Kepler's laws ):

${\displaystyle T={\sqrt {\frac {a^{3}4\pi ^{2}}{G(M+m)}}}\approx {\sqrt {\frac {(1{,}496\cdot 10^{11}~{\rm {m}})^{3}\cdot 4\cdot \pi ^{2}}{6{,}67\cdot 10^{-11}\mathrm {\frac {m^{3}}{kg\,s^{2}}} \cdot 1{,}99\cdot 10^{30}~{\rm {kg}}}}}\approx 3{,}156\cdot 10^{7}~{\rm {s}}\approx 365{,}2~{\rm {Tage}}}$

However, since the vernal equinox is movable because of the precession of the earth's axis and the earth's orbit itself is also subject to disturbances, the movement of the earth can be viewed with reference to different reference points that are moved relative to one another. Depending on which reference point is chosen, there are different numerical values ​​for the length of the year.

• After a sidereal year , the earth again takes up the same position in relation to a fixed star (infinitely far away and imagined without its own motion ). The length of the sidereal year is approximately 365.256 days.
  Meteor streams, for example, always cut the earth's orbit at the same point, provided they are not disturbed . The associated falling star shower is therefore repeated with the period of a sidereal year. The difference between the sidereal year and the tropical year, according to which the calendar is based, is 0.01417 days, so that the passage of the earth through the respective orbit point is one day later in the calendar every 70.6 years. The Perseids are an example of an undisturbed shower. They currently occur around August 12, but were observed in the middle of the 19th century around August 10, at the turn of the first millennium at the end of July and at the beginning of our era around mid-July.
• After a tropical year , the earth takes the same position with respect to the vernal equinox. Since the spring equinox runs towards the earth (see section → Seasons ), the tropical year is a little shorter than the sidereal year and has a duration of about 365.242 days.
  With the period of the tropical year, the seasons repeat. Solar and lunisolar calendars therefore try to use suitable switching rules to adapt the length of their calendar years on average to the tropical year. For a number of more precise but slightly different definitions of the tropical year and the various numerical values ​​associated with it, see tropical year .
• After an anomalous year , the earth has returned to the same position in relation to its perihelion. Since the perihelion moves in a straight line along the orbit, the anomalistic year is slightly longer than the sidereal year and has a duration of about 365.260 days.
• After an eclipse year , the sun, moon and the two nodes of the lunar orbit are again in line. This is one of the conditions for a solar or lunar eclipse. An eclipse results when a new or full moon occurs as a second condition in sufficient time proximity to this configuration. Since the necessary “proximity” covers a period of a good month and two to three new and full moons occur during this period, several eclipses always occur in quick succession as a group (MS, SM, MSM or SMS). Half an eclipse year later, the next eclipse group follows (at the other lunar node). Since the lunar nodes move backwards by about 19 ° during a year due to the precession of the lunar orbit , they come towards the earth's orbit, so that after (on average) 346.620 days eclipses can occur again at the same node. In 2015, for example, the first so-called “eclipse season” is in March / April ( S -M) and the second in September ( S -M). By 2018, the eclipse seasons had already moved forward to January / February (M- S ) and July / August ( S -M- S ).

The mean length of the years mentioned is (for epoch 2012.0):

Sidereal year :	Return to the same star	365 d	6 h	9 m	9.8 s	or	365.256 363 days
Tropical year :	Return to the vernal equinox,	365 d	5 h	48 m	45.2 s	or	365,242 190 days
Anomalous year :	Return to perihelion,	365 d	6 h	13 m	52.6 s	or	365.259 636 days
Eclipse year :	Return to the same lunar node	346 d	14 h	52 m	54.9 s	or	346,620,080 days

Individual years can deviate from these mean values ​​due to disturbances. In addition, the mean length of the year is subject to slow drift due to long-term changes in the earth's orbit.

Seasons

The four Seasons

At the beginning of spring the earth is by definition at the ecliptical longitude 180 °. Seen from the earth, the sun is then at 0 ° (the spring equinox), while the constellations visible at midnight are in the opposite direction at 180 °. These are currently especially the constellations around Leo and Virgo - typical spring constellations . In summer, the constellations around the ecliptical longitude 270 ° are visible at midnight, especially the summer constellations around Sagittarius . Midnight in autumn presents as autumn constellations, among other things, the fish located at a length of 0 ° . At midnight in winter the ecliptical longitude is 90 ° in the sky and with it the Gemini and other winter constellations . (Constellations that are sufficiently close to the celestial pole, such as the Great Bear, are circumpolar and therefore visible in all seasons.)

Since neither the equatorial nor the ecliptic plane is fixed in space due to the gravitational influence of the moon, sun and planets, the inclination of the ecliptic as the intersection of both planes and in particular the position of the vernal equinox on the intersection of both planes are temporally variable. The skewness of the ecliptic fluctuates with a period of about 40,000 years and with an amplitude of about 1 ° around a mean value of about 23 °. The spring equinox precesses once in almost 26,000 years with respect to the fixed star background around the earth's orbit, in the direction opposite to the earth's orbit (retrograde).

From the drift of the vernal equinox along the earth's orbit, it follows that in future the seasons will coincide with other sections of the earth's orbit. After a quarter of the precession period, i.e. in about 6500 years, summer will fall on the section of the orbit in which spring now prevails, and accordingly the current “spring” constellations visible from this orbit section will have become “summer” constellations.

The mentioned changes in eccentricity, ecliptic inclination and the position of the vernal equinox lead in their interaction periodically to stronger or weaker manifestations of the seasons and are therefore probably one of the reasons for the alternation of warm and ice ages (see also: → Milanković cycles ). It is not the position of the vernal equinox in relation to the fixed star background that is important, but its position in relation to the perihelion (for justification see the article → Seasons ). Since the perihelion moves in a straight line around the earth's orbit (see section → Perihelion ), the retrograde vernal equinox meets with it again before it has completed a full orbit with respect to the fixed stars. The mutual positions of the vernal equinox and perihelion are therefore repeated with the already mentioned “climatic” period of only about 21,000 years.

Long term stability

"Chaos"

If one calculates the movement of the planets under the gravitational influence of the sun and the respective other planets over long periods of time, one finds that the outer solar system is essentially stable, while the inner solar system (Mercury, Venus, Earth, Mars) is slightly chaotic (im mathematical sense) . This does not mean that the planets will at some point begin to run randomly (that is, “chaotic” in the colloquial sense). It simply means that small uncertainties in the starting conditions of a long-term calculation build up due to the complex gravitational interactions between the planets and ultimately limit the predictability. For example, an uncertainty of 15 meters in the starting position of the earth leads to an uncertainty of about 150 meters after 10 million years and to an uncertainty of about 150 million kilometers after 100 million years.

It is therefore quite possible to calculate a precise ephemeris of the earth over a period of tens of millions of years. Over longer periods of time, however, the calculated positions become increasingly uncertain, and after a hundred million years at the latest, the uncertainty reaches the dimensions of the earth's orbit itself - it is then no longer possible to predict at which point in its orbit the earth is located. Again, this does not mean that the earth will then be randomly somewhere in the inner solar system. It will still be on its usual path, and the path itself will differ only slightly from today's path within the framework of the disturbances mentioned above. Only the location of the earth on this orbit is no longer predictable from today.

stability

The stability of the solar system would be impaired if the described changes in shape of the planetary orbits - especially a possible strong increase in eccentricities - could lead to close approaches of neighboring orbits in the long term. A planet could then collide with a neighboring planet or be thrown out of its orbit or even out of the solar system if it meets too closely.

As the long-term calculations mentioned above show, such instabilities can be ruled out for the next hundred million years. For the remainder of the solar system's expected lifespan of around 5 billion years, other research methods will have to be used. Because of the increasing uncertainty beyond 100 million years, a single calculation run cannot be regarded as a concrete prediction, but it does represent a possible development. The analysis of an ensemble of orbits (ie numerous calculation runs with slightly different starting conditions) enables statistical estimates of typical ones or at least possible scenarios.

The calculations are simplified if the planets themselves are disregarded and formulas are used for the development of the orbits over time. The slow changes in orbit require less computational effort than the rapidly changing positions of the planets in the orbit, so that an entire ensemble of orbits can be more easily mastered computationally. Corresponding studies showed that over several billion years the eccentricity of the earth's orbit only slightly exceeded its current maximum value of approx. 0.06 and that the orbit of Venus behaved similarly. Mars' eccentricity fluctuates more, but Earth's close encounter with Mars or Venus is not to be expected. Mercury, on the other hand, shows strong fluctuations in eccentricity, so that close encounters with Venus cannot be ruled out in principle.

It has now become possible to use mainframes to calculate the complete planetary movements over several billion years. A study with a total of 2501 calculations, each spanning 5 billion years, showed in the vast majority of cases the same picture as in today's solar system: the planetary orbits are periodically deformed and precess under their mutual interactions, but without the risk of close encounters. In one percent of the cases, the eccentricity of Mercury increased significantly, which then often led to a collision with Venus or the sun, but without noticeably affecting the earth's orbit. Only in one of the 2501 cases, after several billion years, a strongly eccentric Mercury orbit caused a likewise strongly increasing eccentricity of the Mars orbit, which then - depending on the details of the scenario under consideration - enabled the earth to collide with one of the neighboring planets. The statistical details are not undisputed.

Overall, the solar system can be viewed as “marginally stable”: Considerable instabilities (such as a collision) cannot be ruled out in principle, but can at most be expected over periods of several billion years. For the orbits of Earth and Venus, because of the relatively large planetary masses and their mutual coupling, only minor deviations from their current shape are to be expected. They can be viewed as inherently stable during the lifetime of the solar system, provided they are not affected by major instabilities in other planetary orbits.

Sun path

The sun seems to move against the background stars. In fact, the earth moves in such a way that the angle at which the sun is seen against the background changes.

From an earthly perspective, the sun seems to wander through the constellations of the ecliptic over the course of a year, after which the twelve signs of the zodiac are named. This movement of the sun around the earth is known as the apparent geocentric orbit .

For the apparent topocentric orbit of the sun, the sight in the sky perceived by a real observer on earth, see: Sun position

In the celestial mechanical representation, the geocentric position vector of the sun is exactly opposite to the heliocentric position vector of the earth, so the same set of formulas can be used in calculations . This is explained in detail in the article → Sun position .

Track elements

→ Main article : Orbital element

The orbital elements tabulated in the info box of this article correspond to the current state of astronomy. For reasons of space, however, they only show the mean values ​​and are only valid for time J2000.0, so that they are of very limited use for calculating the earth's orbit. A complete representation of the corresponding data record including the path disruptions and the time dependencies is not possible here because of its size. For most practical applications, however, greatly simplified calculation methods are sufficient.

Since the earth's orbit can be described to a good approximation by a Kepler ellipse, the elements of such an ellipse can be used approximately to calculate the position of the earth at a given point in time. The deviations of the earth's orbit from an exact ellipse can be partially taken into account in various ways.

Medium Kepler elements

The following Kepler elements are "middle" elements; H. the periodic orbit disturbances are not taken into account. However, those parts of the disturbances are taken into account that can be described by a linear temporal variation of the mean elements. Higher powers of variation over time are also neglected. As soon as the mean elements for the desired point in time have been determined from the following tables, the usual standard methods can be used to calculate the planetary position from given Kepler elements.

The following set of middle Kepler elements provides the position of the earth-moon center of gravity in relation to the equinox of the date :

a	= 1.000000	AE	major semi-axis
ε	= 0.016709 - 0.000042 * T		Numerical eccentricity
i	= 0.0	°	Orbital inclination in relation to the ecliptic of the date
Ω	not defined		Length of the ascending node (equinox of the date)
ϖ	= 102.9400 + 1.7192 * T	°	Length of perihelion (equinox of date)
M.	= 357.5256 + 35999.0498 * T	°	medium anomaly
L.	= 100.4656 + 36000.7690 * T	°	mean length (equinox of the date), L = M + ϖ

If the position is to be calculated with reference to the equinox J2000.0 , the dependent elements are to be replaced as follows:

i 0	= 0.0 + 0.0131 * T	°	Orbital inclination in relation to the ecliptic of J2000.0
Ω 0	= 174.876-0.242 * T	°	Length of the ascending node (equinox J2000.0)
ϖ 0	= 102.9400 + 0.3222 * T	°	Length of perihelion (equinox J2000.0)
L 0	= 100.4656 + 35999.3720 * T	°	mean length (equinox J2000.0), L 0 = M + ϖ 0

The time T has been measured in Julian centuries since January 1, 2000, 12 ^h DD, so for a Julian day number JD is T = ( JD -2451545.0) / 36525.

Adapted Kepler elements

Another possibility, the earth's orbit, including a portion of the interference approximated by Kepler elements present, is not the middle web elements to determine, but those elements which are the central webs is described (due to the non-linear relationship between the web elements and web, the not the same ). The following Kepler elements were chosen in such a way that the trajectories that follow from them correspond as closely as possible to the actual trajectory over a certain period of time.

Kepler elements for approximate positions of the earth-moon center of gravity, related to the mean ecliptic and the equinox for J2000.0:

1800 - 2050:

a	=	1,000 002 61	+	0.000 005 62 T	AE
ε	=	0.016 711 23	-	0.000 043 92 T	wheel
i	=	−0.000 015 31	-	0.012 946 68 * T.	°
L.	=	100.464 571 66	+	35999,372 449 81 · T	°
ϖ	=	102.937 681 93	+	0.323 273 64 · T	°
Ω	=	0.000 000 00	+	0.000 000 00 T	°

The positions calculated with these elements show errors of the following magnitudes during the specified period 1800–2050: Right ascension 20 ", declination 8", radius vector 6000 km. The elements should not be used outside of this period.

3000 BC Chr. - 3000 AD:

a	=	1,000,000 18	-	0.000 000 03 T	AE
ε	=	0.016 731 63	-	0.000 036 61 T	wheel
i	=	−0.000 543 46	-	0.013 371 78 * T.	°
L.	=	100.466 915 72	+	35999,373 063 29 T	°
ϖ	=	102.930 058 85	+	0.317 952 60 · T	°
Ω	=	−5.112 603 89	-	0.241 238 56 x T	°

The positions calculated using these elements are 3000 BC during the specified period. - 3000 AD Errors of the following orders of magnitude: Right ascension 40 ", declination 15", radius vector 15000 km. The elements should not be used outside of this period.

The time T has been measured in Julian centuries since January 1, 2000, 12 ^h DD, so for a Julian day number JD is T = ( JD -2451545.0) / 36525.

Other orbital representations

If the disturbances are to be fully taken into account, but the orbit should still be represented by Kepler elements, then oscillating Kepler elements can be used, which describe the Kepler ellipse that best fits the real, disturbed orbit at the current location of the planet . The oscillating elements can be changed relatively quickly because of the disturbances and must therefore be tabulated on a correspondingly fine time grid. The Astronomical Almanac contains on page E7 the oscillating elements of the earth's orbit for the respective year on a 40-day grid.

Instead of using Kepler elements, a planetary orbit can also be represented by series expansion for length, width and radius vector. The disturbances can be taken into account by adding suitable terms. Exact path representations can contain many thousands of terms, but if the accuracy requirements are lower, the calculation can be aborted as soon as the desired accuracy is achieved. The short series development according to van Flandern and Pulkkinen, intended for everyday demands, achieves an accuracy of about one arc minute over the period from about 300 years ago to 300 years after the present. More complex series developments are z. B. the VSOP87 and the VSOP2013 .

The most accurate calculation of ephemeris is achieved by numerically solving the equations of motion . The result is a table with tabulated planetary positions from which the user can read the position for the desired point in time. Examples are the various "Development Ephemeris" DExxx of   the JPL , the "Integration Numerique Planetaire de l'Observatoire de Paris" INPOP of   the IMCCE , or the "Ephemerides of Planets and the Moon" EPM of   the Institute for Applied Astronomy of the Russian Academy of Sciences .

Coordinate objects

The earth is accompanied by some co-ordinate objects on its orbit around the sun . These small celestial bodies orbit the sun on orbits on which they have a similar or even the same orbital period as the earth. Due to the low relative speed and with the help of resonance effects , the gravitational pull of the earth can hold these objects more or less permanently in their co-ordinate orbits.

The earth is directing the near-earth asteroid Cruithne into a horseshoe orbit along the earth's orbit. The asteroid 2003 YN ₁₀₇ was a quasi-satellite of the earth from 1996 to 2006 and will be captured by the earth as a real second moon at the next but one encounter in the year 2120. The co-ordinate asteroid 2002 AA ₂₉ alternates approximately cyclically between a horseshoe orbit and a quasi-satellite orbit, and the next time around the year 2600 it will be a quasi-satellite for 45 years.

In October 2010, another co-ordinate object was discovered with 2010 TK ₇ , which in July 2011 was the first Trojan horse on earth to be detected. The approx. 300 m large asteroid circles on a stable orbit around the Lagrange point L ₄ and thus 60 ° in front of the earth on its orbit around the sun.

See also

• Heliocentric worldview
• Lunar orbit
• Planetary orbit
• Precession
• Sun apex

Web links

Wiktionary: Earth orbit  - explanations of meanings, word origins, synonyms, translations

• WEBGEO module: Earth, orbit, astronomical seasons - WEBGEO - E-learning portal for geography and related sciences

Remarks

1. ↑ The apparent daily migration of the sun across the sky is only due to the rotation of the earth: the sun moves here together with the fixed stars across the sky, approximately parallel to the equator, not along the ecliptic.
2. ↑ When the Earth passes through this point in the winter, she sees the sun at the opposite point in the constellation Sagittarius are
3. ↑ ^{a b} The coefficients of t given in the source in arc seconds have been converted into degrees by dividing with 3600 for better readability.
4. ↑ The symbol ϖ is not an ω ( omega ) with a tilde, but an italic π ( pi ).
5. ↑ For the sake of comparability, the information prior to the Gregorian calendar reform was converted to a fictitious proleptic Gregorian calendar.
6. ↑ For T <0 denote i ₀ the negative orbital inclination and Ω ₀ the descending node. This avoids the actually existing but computationally impractical jump in Ω ₀ when the current ecliptic penetrates the ecliptic of J2000.0.

Individual evidence

1. ↑ ^{a b c d e f g h} J. L. Simon, P. Bretagnon, J. Chapront, M. Chapront-Touzé, G. Francou, J. Laskar: Numerical expressions for precession formulas and mean elements for the Moon and the planets. In: Astronomy and Astrophysics. vol. 282, 1994, pp. 663-683. (on-line)
2. ↑ ^{a b} IMCCE: Le manuel des éclipses. EDP ​​Sciences, Les Ulis 2005, ISBN 2-86883-810-3 , p. 27: Mean orbital elements of the earth for epoch J2000. (on-line)
3. ↑ ^{a b} A. Lehnen, J. Kessenich: Moments of the Distance from the Force Center in a Two-Body Kepler Orbit. Table 4 ( online , accessed January 20, 2015)
4. ↑ ^{a b c d} NASA: Earth Fact Sheet (accessed November 19, 2014)
5. ↑ Perihelion distance = a (1 - e ), aphelion distance = a (1 + e ).
6. ↑ JB Tatum: Celestial Mechanics chap. 9 ( PDF 203 kB ): < r > = a (1 + 1/2 e ² ), accessed on January 9, 2015
7. ↑ PK Seidelmann (Ed.): Explanatory Supplement to the Astronomical Almanac. University Science Books, Mill Valley 1992, ISBN 0-935702-68-7 , p. 700.
8. ^ J. Meeus: Astronomical Algorithms. 2nd Edition. Willmann-Bell, Richmond 2000, ISBN 0-943396-61-1 , chap. The circumference of an ellipse having semimajor axis 33 a and the eccentricity e is L = 2 π a [1 - e ² /4 - 3/64 e ⁴ - 45/2304 e ⁶ - ...]
9. ↑ 90 ° minus skew of the ecliptic (23 ° 26 '21.412 "according to Simon et al .: Numerical expressions ... )
10. ^ AN Cox (Ed.): Allen's Astrophysical Quantities. 4th edition. Springer Science + Business Media, New York 2004, ISBN 0-387-98746-0 , p. 12.
11. ^ ^{A b c} J. Meeus: More Mathematical Astronomy Morsels. Willmann-Bell, Richmond 2002, ISBN 0-943396-74-3 , chap. 33
12. ↑ ^{a b c} A. Berger, MF Loutre: Precession, Eccentricity, Obliquity, Insolation and Paleoclimates. In: J.-C. Duplessy, M.-T. Spyridakis (Ed.): Long-Term Climatic Variations. NATO ASI Series, Volume I 22 (1994) pp. 107–152 ( PDF , 5.1 MB). The time average of ( a / r ) ² is . ${\displaystyle \textstyle \left\langle {\frac {a^{2}}{r^{2}}}\right\rangle \,=\,{\frac {1}{T}}\int _{0}^{T}\left({\frac {a}{r}}\right)^{2}dt\,=\,{\frac {1}{\sqrt {1-\varepsilon ^{2}}}}}$
13. ^ J. Meeus: Mathematical Astronomy Morsels. Willmann-Bell, Richmond 1997, ISBN 0-943396-51-4 , chap. 27
14. ↑ Eva Bauer: Climatic Factors and Climatic Changes in the Last Millennium. In: Stars and Space. December 2005, pp. 31-38. PDF (932 kB) ( Memento from March 4, 2016 in the Internet Archive )
15. ^ ^{A b} J. Meeus: Astronomical Algorithms. 2nd Edition. Willmann-Bell, Richmond 2000, ISBN 0-943396-61-1 , chap. 31
16. ↑ AJJ van Woerkom: Note about galactic precession. In: Bulletin of the Astronomical Institutes of the Netherlands. Volume 9, (1943), p. 427 (online)
17. ↑ RS steadly, MS Robinson (ed.): The Astronomical Almanac for the Year 2012 US Government Printing Office, ISBN 978-0-7077-4121-5 , page E2.
18. ^ WM Owen, Jr .: A Theory of the Earth's Precession Relative to the Invariable Plane of the Solar System. Dissertation, University of Florida 1990, Fig. 5–1, p. 253 (online)
19. ↑ D. Souami, J. Souchay: The solar system's invariable plane. In: Astronomy & Astrophysics. Volume 543, July 2012, article no. A133, doi: 10.1051 / 0004-6361 / 201219011
20. ↑ ^{a b c} P. K. Seidelmann (Ed.): Explanatory Supplement to the Astronomical Almanac. University Science Books, Mill Valley 1992, ISBN 0-935702-68-7 , p. 99.
21. ^ ^{A b} S. E. Urban, PK Seidelmann (Ed.): Explanatory Supplement to the Astronomical Almanac. 3. Edition. University Science Books, Mill Valley 2013, ISBN 978-1-891389-85-6 , p. 212.
22. ^ ^{A b} J. Meeus: More Mathematical Astronomy Morsels. Willmann-Bell, Richmond 2002, ISBN 0-943396-74-3 , chap. 27
23. ↑ J. Laskar, P. Robutel, F. Joutel, M. Gastineau, ACM Correia, B. Levrard: A long-term numerical solution for the insolation quantities of the Earth. Astronomy & Astrophysics 428, 261-285 (2004), doi : 10.1051 / 0004-6361: 20041335 , pp. 268ff and Fig. 11
24. ^ DW Hughes, B. Emerson: The stability of the node of the Perseid meteor stream. In: The Observatory. Volume 102, 1982, pp. 39-42. (on-line)
25. ↑ IMCCE: Le manuel des éclipses. EDP ​​Sciences, Les Ulis 2005, ISBN 2-86883-810-3 , pp. 85ff.
26. ↑ RS Steadly, MS Robinson (Ed.): The Astronomical Almanac for the Year 2012. US Government Printing Office, ISBN 978-0-7077-4121-5 , p. C2.
27. ↑ ^{a b} J. Laskar: Is the Solar System stable? In: Progress in Mathematical Physics. 66, 2013, pp. 239–270 ( preprint , p. 19)
28. ^ ^{A b} J. Laskar: Large Scale Chaos and Marginal Stability in the Solar System. In: Celestial Mechanics and Dynamical Astronomy. Volume 64, 1996, No. 1-2, pp. 115-162 (online) , pp. 147ff.
29. ↑ J. Laskar: Is the Solar System stable? In: Progress in Mathematical Physics. 66, 2013, pp. 239–270 ( preprint , p. 27)
30. ^ RE Zeebe: Dynamic stability of the Solar System: Statistically inconclusive results from ensemble integrations. In: The Astrophysical Journal. accepted ( arxiv : 1506.07602 preprint)
31. ^ ^{A b} J. Laskar: Large Scale Chaos and Marginal Stability in the Solar System. In: Celestial Mechanics and Dynamical Astronomy. Volume 64, 1996, Issue 1-2, pp. 115-162 (online) , p. 155.
32. ↑ ^{a b} O. Montenbruck: Basics of the ephemeris calculation. 6th edition. Verlag Sterne und Weltraum, Heidelberg 2001, ISBN 3-87973-941-2 , p. 139.
33. ↑ ^{a b c} S. E. Urban, PK Seidelmann (ed.): Explanatory Supplement to the Astronomical Almanac. 3. Edition. University Science Books, Mill Valley 2013, ISBN 978-1-891389-85-6 , p. 338 (Chapter 8.10: Keplerian Elements for Approximate Positions of the Major Planets. ) ( Preprint, PDF 68 kB )
34. ↑ TC Van Flandern, KF Pulkkinen: Low-precision Formulas for Planetary Positions. In: Astrophysical Journal Supplement Series. Volume 41 (Nov. 1979) pp. 391-411 (online)
35. ↑ Ephemeris files on the JPL's FTP server: [1] (see README.txt)
36. ↑ JPL's ephemeris server for direct retrieval of planetary positions: ssd.jpl.nasa.gov
37. ↑ IMCCE: INPOP13c, a 4-D planetary ephemeris (accessed January 8, 2015)
38. ↑ EV Pitjeva: Updated IAA RAS Planetary Ephemerides-EPM2011 and Their Use in Scientific Research. In: Solar System Research. Volume 47, Issue 5, September 2013, pp. 386-402. ( doi: 10.1134 / S0038094613040059 , preprint )