Apse rotation


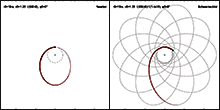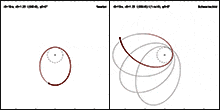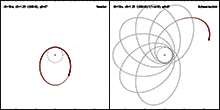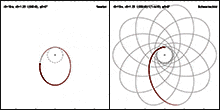
The apse rotation of an elliptical orbit is a progressive rotation of the entire orbit in the plane of the orbit . The vestibule line rotates continuously, while the shape and level of the path in space remain the same. Depending on the central body, the following terms are also used:
- Perihelion rotation , or also precession of the perihelion , when the orbit revolves around the sun and
- Perigee rotation , when the orbit revolves around the earth, i.e. the perigee is considered.
If this movement is sometimes referred to as the "precession" of the pericenter, it must not be confused with the similar sounding precession of the equinoxes , which is also an orbital disruption but affects the position of a plane in space.
causes
An apse rotation occurs when a celestial body is subject to certain external disturbances on its elliptical orbit around a central body . If the celestial body were exposed to an attraction which, strictly inversely, decreases quadratically with the distance from the central body, it would move exactly on a Keplerellipse whose shape, position and orientation in space would remain unchanged. According to Bertrand's theorem, the only centrally symmetric potentials with closed paths are the 1 ⁄ r potential and the potential of the harmonic oscillator with a radial function proportional to r². However, deviations from the strictly inverse-quadratic law of force lead to various types of path disturbances , which can change the shape, position and orientation of the path. One of these path disturbances is the rotation of the vestibule.
- A possible cause for deviations from the 1 ⁄ r 2 law of central force is the presence of other bodies, which exert additional gravitational forces on the celestial body under consideration. In the case of the planetary orbits, the influence of the other planets is the main cause of the perihelion rotations.
- Another cause may be deviations of the central body from the spherical shape . While an exactly spherically symmetrical extended body would generate the same strictly inverse-quadratic gravitational field as a point-shaped body of the same mass, irregular mass distributions or the equatorial bulge of flattened central bodies lead in turn to deviations from the inverse-quadratic law of force and thus to path disturbances. The earth's equatorial bulge causes (among other orbital disturbances) perigee rotations in artificial earth satellites . The flattening of the sun causes perihelion rotations of the planetary orbits, which due to the insignificance of the flattening and the large distance between the planets are much smaller than the rotations caused by the planets among each other.
- The curvature of spacetime, an effect of the general theory of relativity , causes a deviation from Newton's equations of motion (see effective potential # general relativity ). This creates a contribution to the perihelion rotation, which is called the Schwarzschild precession.
- There are hypotheses that the idealized force law itself deviates from the inverse-quadratic behavior (e.g. the modified Newtonian dynamics ). This would also contribute to the rotation of the vestibule.
Results from all these causes - in relation to the fixed star background resting coordinate system - a rosette-like movement of the body: The anomalistic period does not correspond exactly to the sidereal . In celestial mechanics this is described by a long-period term of the orbit element argument of the pericenter .
If the path is not described in a reference system at rest with respect to the fixed star background, but in a rotating reference system, an additional apparent rotation is added to the physically caused rotations described above, which merely reflects the rotation of the reference system. In the case of the planetary orbits of the solar system, the perihelion rotations - counted from a fixed spring point - are only fractions of a degree per century. If, on the other hand, the orbits are described with reference to the moving equinox of the date , their speeds in this rotating reference system are higher by the precession speed of the vernal equinox, namely 1.396 ° per century, and are between one and two degrees per century.
Episodes from the history of research
Movement of the apogees
It was already known to ancient astronomers through observation that the sun, moon and planets did not move through their orbits at constant speeds. Greek astronomers took this into account in their planetary theories by making the center of the respective planetary orbit, assumed to be circular, not coincide with the center of the earth assumed to be in the center of the universe, but in a suitable direction by a certain amount (the so-called eccentricity , not to be confused with the eccentricity of an elliptical path). On the half of the orbit that is closer to the observer, the steadily rotating planet now apparently moved faster than on the opposite half. As can be shown, the real speed curve of a planet, following Kepler's second law , can be computationally reproduced in a very good approximation by means of a suitably shifted circular path (a so-called eccentric ). Hipparchus, for example, deduced from the unequal lengths of the seasons on the speed variation of the sun (then treated as a planet) in the individual orbital quadrants and described its orbit by a circle that was shifted by 1/24 of its radius in the direction of 65.5 °. The apogee of the sun's orbit was in this direction , the ecliptical length of which was actually 66.23 ° at that time. (At that time the apogee was used as a reference point, whereas today the perigee is preferred.)
Ptolemy repeated the orbit determination 300 years later. But since his observations showed the same lengths for the seasons, he also received the same solar orbit and therefore considered the position of their apogee to be unchangeable with regard to the equinox :
"We also come to the result that even today the times of the above-mentioned quadrants and the specified ratios are almost the same, from which we can see that the eccentric of the sun at the infinite and equinoxes always maintains the same position."
However, the apogee of the other planets behaved differently. From the results of numerous observations and evaluations, he concluded that their apogee is not based on the equinox, but on the fixed stars. This is remarkable insofar as, in his view (and in contrast to today's point of view), the equinoxes were regarded as stationary and the fixed stars as moved as a result of precession. Accordingly, he believed the apogees to be agile and their speed had to be determined. The observations showed him that they are all about the same fast rechtläufig moving and that their speed as the Observatory accuracy consistent with the precession of the stars; he found that
"Also the apogee of the eccentrics bring about a very small progress from the turning points in the direction of the signs, which again runs uniformly around the center of the ecliptic and is roughly the same for all planets as it was perceived in the sphere of the fixed stars - d. H. in 100 years of the amount of one degree - as far as it is at least possible to gain an insight from the available material. "
In the 9th century Thabit ibn Qurrah noticed that the sun apogee also carried out a right-hand movement with respect to the equinox. Like that of the planetary apogees, this movement was initially thought to be purely due to the precession. Al-Battani, for example, set the solar apogee for March 1, 880 at 82 ° 15 'ecliptical longitude and gave the instruction to add or subtract 1 ° precession shift to calculate the apogee longitude at other times for every 66 elapsed years:
"The apogee moves with the same movement with which the fixed star sphere rotates and which we have established through observation that it is 1 degree in 66 Roman years."
The same was true for him, as it was for Ptolemy, for the apogee of the planets:
"The [lengths of these] apogees move with the movement of the fixed star sphere, namely one degree in 66 solar years."
It was not until Ibn al-Shatir observed in the 14th century that the solar apogee did not move exactly with the speed of precession (namely 1 ° per 60 Persian years compared to 1 ° per 70 Persian years), i.e. moved independently with regard to the fixed stars .
In contrast to the planetary orbits, the perigee rotation of the moon was already known to the Babylonian astronomers and explicitly included in their calculation schemes. Hipparchus and Ptolemy took basic numerical values from Babylonian astronomy and worked them out into detailed lunar theories based on the epicyclic model .
Perihelion of Mercury
The elliptical shape of the planetary orbits was first described empirically in 1609 by Kepler's laws . The physical justification followed in the middle of the 17th century with the celestial mechanics of Isaac Newton . With his universal law of force, which also describes gravity , it was possible to investigate the orbital disturbances that the planets mutually cause. In particular, the observed rotations of the apses of the planets and the moon could be almost completely explained by Newton's theory.
In the middle of the 19th century, however, Urbain Le Verrier used observations of Mercury transits for a particularly precise measurement of Mercury's orbit and found on the basis of the improved data that the perihelion of Mercury was slightly stronger than expected. According to the celestial mechanical calculations, it should be around 530 ″ ( arcseconds ) per century, with around 280 ″ due to the influence of Venus, around 150 ″ due to disturbances by Jupiter and around 100 ″ on the other planets. The observed perihelion rotation (modern value: 571.91 ″ / century) was, however, significantly greater; the modern value for the discrepancy is 43.11 ″.
Le Verrier, who had already successfully made the discovery of Neptune possible through the investigation of unexplained components in the orbit faults of Uranus , suspected that the cause of the discrepancy in Mercury was a disturbance by a previously unknown planet on a orbit within Mercury's orbit. This planet was given the name volcano , but could not be discovered despite an extensive search - including during several solar eclipses . Likewise, no asteroid belts close to the sun responsible for the disturbances could be detected. Others suspected the dust belt responsible for the zodiacal light or saw at least part of the cause in a flattened shape of the sun due to its rotation (see also below), but their attempts to explain it were also unsuccessful.
Further attempts at explanation cast doubt on the validity of Newton's law of force. For example, Levy (1890) and above all Paul Gerber (1898) succeeded in completely deriving the excess on the basis of electrodynamic laws of force , provided that the speed of propagation of gravity is equal to the speed of light . Gerber's formula for the perihelion deviation was already formally identical to that later drawn up by Einstein. However, the underlying force laws were wrong and theories of this kind had to be rejected.
Only Albert Einstein's general theory of relativity , which describes gravity as the curvature of space-time , on the structure of which the celestial bodies also influence, could convincingly explain the excess. This success is considered to be one of the mainstays of general relativity and its first major confirmation. The relativistically calculated portion of 42.98 ″ agrees very well with the observed excess of 43.11 ″. The reason for the relativistic effect lies in the slight deviation of the relativistically treated gravitational field from the strictly inverse-quadratic behavior.
The agreement between observation and relativistic calculation would be less good if a noticeable part of the observed excess could be attributed to a rotation-related flattening of the sun and the remaining part to be explained would therefore be significantly lower than calculated according to ART. Attempts to measure the extremely low level of flattening of the sun produced contradicting results over a long period of time, so that it was always a little doubtful how good the correlation between the relativistic forecast and the observation actually was. However, helioseismological studies have meanwhile reliably determined the quadrupole moment of the sun to be (2.18 ± 0.06) · 10 −7 ; this quadrupole moment only contributes a few hundredths of an arc second to the rotation of the perihelion and is therefore negligible. Another possibility for determining uses the fact that the relativistic and the conditional share of the total rotation of the perihelion decrease at different rates with increasing distance from the sun and can thus be separated from each other by comparing the total rotations of different planets. Such a study gave a result of = (1.9 ± 0.3) · 10 −7 , which is close to that of helioseismology.
The table lists some observation results of the perihelion rotation from the last decades:
| year | Authors | method | Rotation per century | source |
|---|---|---|---|---|
| 1975 | Morrison, Ward | Mercury passages | 41.9 ″ ± 0.5 ″ | |
| 1976 | Shapiro et al. a. | radar | 43.11 ″ ± 0.21 ″ | |
| 1987 | Anderson et al. a. | radar | 42.92 ″ ± 0.20 ″ | |
| 1991 | Anderson et al. a. | radar | 42.94 ″ ± 0.20 ″ | |
| 1992 | Anderson et al. a. | radar | 43.13 ″ ± 0.14 ″ |
Examples
Planetary orbits
The orbits of all planets in the solar system are subject to continuous perihelion rotations in the direction of orbital motion, mainly because of their mutual interference. The following table lists the amounts of these rotations both with regard to the vernal equinox (“tropical”) and with regard to the fixed star background (“sidereal”). The numerical values are slightly changeable in the long term and are also subject to slight, shorter-term fluctuations. The specified values describe the mean movement (i.e. taking account of the short-term fluctuations) for the beginning of the year 2000 (i.e. for epoch J2000.0 ).
| planet | tropical [° / century] | sidereal [° / century] |
|---|---|---|
| Mercury | 1.556 | 0.159 |
| Venus | 1.402 | 0.005 |
| earth | 1.720 | 0.323 |
| Mars | 1,841 | 0.444 |
| Jupiter | 1.613 | 0.216 |
| Saturn | 1.964 | 0.567 |
| Uranus | 1.486 | 0.089 |
| Neptune | 1,426 | 0.029 |
The numerical values of both columns differ by 1.396 ° per century, the rate of precession of the earth in ecliptical longitude. For example, the angle between the earth's perihelion and the vernal equinox changes by 1.720 ° / century, so that after about 21,000 years both of them assume the same position to each other again, which could have effects on the climate, among other things (see Ice Age , Milanković cycles ). However, this cycle is mainly determined by the faster movement of the vernal equinox. The angle between the perihelion and a fixed star (thought to be infinitely distant), on the other hand, only changes at a rate of 0.323 ° / century, so that the perihelion needs about 110,000 years to orbit the earth's orbit with respect to inertial space . This is the rate of perihelion movement as caused by external disturbances.
The extent of the perihelion rotation depends, among other things, on the eccentricity of the orbit in question. Venus, with its almost circular orbit, therefore shows a remarkably small sidereal perihelion rotation.
moon
The apsidal line of the moon rotates around the entire lunar orbit once every 8.85 years. The main cause for this is the sun, which acts as the third, disruptive body on the moon's orbit around the earth.
This cycle of the apses ( English lunar apse cycle, perigee cycle ) is calculated:
The cycle is found in the variation of the lunations and has also been studied as a period of the tides and meteorological phenomena.
Artificial earth satellites
Perigee rotations of satellites are represented as a basic satellite orbit element. Their cause lies in the flattening of the earth and, in the case of satellites in low orbit, also in atmospheric friction. The perigee rotation of the GPS satellites , which orbit the earth at an altitude of around 20,200 kilometers, is around 0.01 ° per day.
If one describes the deviation of the earth's gravitational potential from the spherical shape in a simplified manner by restricting it to its quadrupole moment , then the movement of the perigee amounts to
| mean movement of the satellite | |
| major semi-axis of the earth (6,378,137 m) | |
| semi-major axis of orbit | |
| Orbit inclination | |
| Orbit eccentricity | |
| Expansion coefficient of the quadrupole moment of the earth's gravitational potential (1.0826359 · 10 −3 ) |
For slopes below 63.4 °, the perigee moves in the direction of movement of the satellite. For inclinations above it, it moves downwards. If the satellite has an orbit inclination of 63.4 °, it is (approximately) not subject to any perigee rotation, because . If its orbital duration is about 12 hours (more precisely: half a sidereal day ) and if the orbit is chosen to be very eccentric, the apogee is longer over the same region of the earth's surface during each orbit and the satellite can, for example, be used favorably for telecommunication purposes. It is in what is known as a Molnija orbit .
Relativistic perihelion
In addition to Mercury , the relativistic part of the perihelion rotation could also be demonstrated for Venus , Earth , Mars and the asteroid Icarus (see table, as of 1986). For example, the Earth's total observed rotation is 1161 ″ per century; this is 5 ″ more than is to be expected according to Newton's theory of gravity. This excess is well compatible with the relativistic forecast of 3.8 ″.
| body | Rotation per century relativistic share |
|
|---|---|---|
| theory | observation | |
| Mercury | 42.98 ″ | 43.11 ″ ± 0.45 ″ |
| Venus | 8.6 ″ | 8.4 ″ ± 4.8 ″ |
| earth | 3.8 ″ | 5.0 ″ ± 1.2 ″ |
| Mars | 1.4 ″ | 1.5 ″ ± 0.15 ″ |
| Icarus | 10.3 ″ | 9.8 ″ ± 0.8 ″ |
For the relativistic perihelion of a planet, the following applies:
| Newtonian constant of gravity | Solar mass | |||
| Gaussian gravitational constant : 0.01720209895 AE 3/2 d −1 M S −1/2 | Number of seconds in the day: 86400 s | |||
| Astronomical unit in meters: AU = 1.4959787 · 10 11 m | Speed of light : 299792458 m / s | |||
| major semi-axis of the planet in meters | major semi-axis of the planet in AE | |||
| Eccentricity of the planetary orbit | Orbit period of the planet in years | |||
| Perihelion rotation, radians per year |
The second form of the equation results when the heliocentric gravitational constant is expressed by the Gaussian gravitational constant .
With the orbital data = 0.387099 AU, = 0.205630 and = 0.24085 years for Mercury, for example, one obtains the perihelion rotation of 42.98 arc seconds per 100 years given in the table.
Exotic systems
In extreme form, the rotation of the apses occurs between particularly massive celestial bodies such as stars and neutron stars . In the double pulsar PSR 1913 + 16 the relativistic perihelion rotation is 4.2 ° per year, in the double system PSR J1906 + 0746 it is 7.57 ° per year, and in PSR J0737-3039 (in which both components are pulsars) it is even 16.90 ° per year.
The light curve of quasar OJ 287 suggests that there are two black holes orbiting each other in its center , whose mutual orbit rotates by 39 ° per 12-year orbit.
For a long time the apsidal rotation of the binary star system DI Herculis seemed to contradict the laws of physics, but the slow speed of the apsidic rotation is caused by the position of the axis of rotation in the plane of the orbit.
literature
- (al-Battani 900): M. al-Battani: Zij . Ar-Raqqah, about 900; Latin translation: CA Nallino: Al-Battani sive Albatenii Opus Astronomicum . Milan 1899-1907; Reprinted by Olms, Hildesheim 1977
- (Anderson 1987): JD Anderson, G. Colombo, PB Espsitio, EL Lau, GB Trager: The mass, gravity field, and ephemeris of Mercury . In: Icarus , 71, 1987, p. 337
- (Anderson 1991): JD Anderson, MA Slade, RF Jurgens, EL Lau, XX Newhall, EM Standish Jr .: Radar and Spacecraft Ranging to Mercury between 1966 and 1988 . In: Proc. ASA , 9, 1991, p. 324
- (Anderson 1992): JD Anderson et al .: Recent Developments in Solar-System Tests of General Relativity . In: H. Sato, T. Nakamura (eds.): Proc. Sixth Marcel Grossmann Meeting . World Scientific, Singapore (1992)
- (Burgay 2003): M. Burgay: An increased estimate of the merger rate of double neutron stars from observations of a highly relativistic system . In: Nature , 426, 2003, pp. 531-533, Abstract , arxiv : astro-ph / 0312071
- (Dehnen 1988): H. Dehnen: Empirical foundations and experimental testing of the theory of relativity . In: J. Audretsch, K. Mainzer (Ed.): Philosophy and Physics of Space-Time . Basics of the exact natural sciences, Volume 7. BI-Wissenschaftsverlag 1988
- (Einstein 1915): A. Einstein: Explanation of the perihelion movement of Mercury from the general theory of relativity . In: Meeting reports of the Prussian Academy of Sciences , 1915, pp. 831–839
- (Freundlich 1915): E. Freundlich: About the explanation of the anomalies in the planetary system by the gravitational effect of interplanetary masses . In: Astronomische Nachrichten Nr. 4803, Vol. 201, 1915, pp. 49-56, bibcode : 1915AN .... 201 ... 49F
- (Guthmann 2000): A. Guthmann: Introduction to celestial mechanics and ephemeris calculation . 2nd Edition. Spectrum, Heidelberg 2000, ISBN 3-8274-0574-2
- (Hofmann-Wellenhof 1997): B. Hofmann-Wellenhof et al .: GPS - Theory and Practice . 4th edition. Springer, Vienna 1997, ISBN 3-211-82839-7
- (Kramer 2006): M. Kramer et al .: Tests of general relativity from timing the double pulsar . In: Science Express , Sept. 14, 2006, arxiv : astro-ph / 0609417
- (Lorimer 2006): DR Lorimer et al .: Arecibo Pulsar Survey Using ALFA. II. The Young, Highly Relativistic Binary Pulsar J1906 + 0746 . In: ApJ , 640, 2006, pp. 428–434 ( abstract )
- (Meeus 2000): J. Meeus: Astronomical Algorithms . 2nd ed., 2nd prnt., Willmann-Bell, Richmond 2000, ISBN 0-943396-61-1
- (Morrison Ward 1975): LV Morrison, CG Ward: An Analysis of the Transits of Mercury: 1677-1973 . In: Mon. Not. R. astr. Soc. , 173, 1975, pp. 183-206, bibcode : 1975MNRAS.173..183M
- (Neugebauer 1975): O. Neugebauer: A History of Ancient Mathematical Astronomy . Springer, Berlin 1975, ISBN 3-540-06995-X
- (Nobili 1986): A. Nobili, C. Will: The real value of Mercury's perihelion advance . In: Nature , 320, 1986, pp. 39-41, bibcode : 1986Natur.320 ... 39N
- S. Oppenheim: Critique of Newton's Law of Gravitation . In: Encyclopedia of Mathematical Sciences, including its applications . 6.2.2, 1920, pp. 80-158.
- (Pedersen 1974): O. Pedersen: A Survey of the Almagest . Odense University Press, 1974
- (Pijpers 1998): FP Pijpers: Helioseismic determination of the solar gravitational quadrupole moment . In: Mon. Not. R. Astron. Soc. , 297, 1998, pp. L76-L80, bibcode : 1998MNRAS.297L..76P
- (Pitjeva 2005): EV Pitjeva: Relativistic Effects and Solar Oblateness from Radar Observations of Planets and Spacecraft . In: Astronomy Letters , 31, 2005, Volume 5, pp. 340-349, bibcode : 2005AstL ... 31..340P
- (Ptolemy 150): C. Ptolemy: Almagest . Alexandria, about 150; German translation: Handbook of Astronomy (translated by K. Manitius). Teubner, Leipzig 1963
- N. T Roseveare: Mercury's perihelion from Leverrier to Einstein . University Press, Oxford 1982.
- (Saliba 1994): G. Saliba: A History of Arabic Astronomy . New York University Press, New York 1994, ISBN 0-8147-7962-X
- (Shapiro 1976) II Shapiro, CC Counselman III, RW King: Verification of the principle of equivalence for massive bodies . In: Phys. Rev. Lett. , 36, 1976, p. 555
- (Sivaram 1995): C. Sivaram: The Hulse-Taylor binary pulsar PSR1913 + 16 . In: Bull. Astr. Soc. India , 23, 1995, pp. 77-83, bibcode : 1995BASI ... 23 ... 77S
- (Will 1993): CM Will: Theory and Experiment in Gravitational Physics . Revised edition, Cambridge University Press, Cambridge 1993, ISBN 0-521-43973-6
- (Will 2006): CM Will: The Confrontation Between General Relativity and Experiment . In: Living Rev. Relativity , 9, 2006, arxiv : gr-qc / 0510072
Web links
Individual evidence
- ↑ (Ptolemy 150) Book 3, chap. 4th
- ↑ (Pedersen 1974) p. 147
- ↑ (Ptolemy 150) Book 3, chap. 4; Manitius Vol. I p. 167
- ↑ (Ptolemy 150) Book 3, chap. 5; Manitius Vol. II p. 121
- ↑ (Neugebauer 1975) p. 58
- ↑ (al-Battani 900) p. 72 (Apogeum enim eodem motu quo sphaera stellarum fixarum volvitur, movetur, quem observationibus invenimus unius gradus esse in 66 annis Romanis […] ", own translation)
- ↑ (al-Battani 900) p. 114 (Horum apogeorum [longitudines] motu sphaerae stellarum fixarum moventur, scilicet uno gradu in 66 annis solaribus […] ", own translation).
- ↑ (Saliba 1994) p. 234
- ↑ (Neugebauer 1975) p. 480
- ↑ (Neugebauer 1975) p. 71
- ↑ (Will 1993), p. 181
- ↑ (Meeus 2000) chap. 31
- ↑ cf. for example (Freundlich 1915)
- ^ Oppenheim (1920), 153ff.
- ↑ Roseveare (1982), chap. 6th
- ↑ (Einstein 1915)
- ↑ a b (Nobili 1986)
- ↑ (Guthmann 2000) p. 93ff
- ↑ (Will 2006) p. 38
- ↑ (Pitjeva 2005)
- ↑ (Morrison Ward 1975)
- ↑ (Shapiro 1976), quoted from (Pijpers 1998)
- ↑ (Anderson 1987), quoted from (Pijper 1998)
- ↑ (Anderson 1991)
- ↑ (Anderson 1992), quoted from (Pijper 1998)
- ↑ (Meeus 2000) chap. 31, figures rounded
- ↑ (Neugebauer 1975) p. 1103ff
- ^ Nautical Almanac . 1974, p. 107 . ; quoted after Victor Reijs: Mean lunar and solar periods. In: The Moon and its path. February 23, 2001, accessed May 9, 2010 .
- ↑ First research by Otto Pettersson: On the occurrence of lunar periods in solar activity and the climate of the earth. A study in geophysics and cosmic physics . In: Svenska Hydrogr. Biol. Come on . 1914 (English). ; derslb .: Long periodical variations of the tide-generating force . In: Conseil Permanente International pour l'Exploration de la Mer (ed.): Pub. Circ. No. 65 , p. 2-23 (English). ; cited n. and further literature: John E. Sanders (Barnard College, Columbia University): The Lunar Perigee-syzygy Cycle for 1998: Implications for Astronomic Tidal Heights . (English, ess.sunysb.edu [PDF; accessed on May 9, 2010]). ; derslb .: Lunar Cycles - 1999 . (English, geo.sunysb.edu [PDF]).
- ↑ a b (Hofmann-Wellenhof 1997) p. 62
- ↑ International Earth Rotation & Reference Systems Service: Useful Constants , accessed August 15, 2006
- ↑ (Nobili 1986), quoted from (Dehnen 1988)
- ↑ (Sivaram 1995), (Will 2006) chap. 5
- ↑ (Lorimer 2006), (Will 2006) chap. 5
- ↑ (Burgay 2003), (Will 2006) chap. 5, (Kramer 2006)
- ↑ MJ Valtonen et al .: Confirmation of the Gravitational Wave Energy Loss in the Binary Black Hole System OJ287 . American Astronomical Society, AAS Meeting # 211, # 112.07 (2007), bibcode : 2007AAS ... 21111207V
- ↑ S. Albrecht, S. Reffert, I. Snellen, J. Winn: Nature 461, 373-376 (2009)