Precession
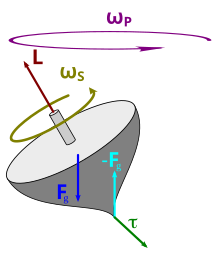
The precession is the change in direction which the axis of rotation of a rotating body ( gyro executes) when an external force is a torque exerted perpendicular to said axis. The axis of rotation describes a revolution on the jacket of an imaginary cone with a fixed cone axis. The precession is clearly shown with the table top, which does not tip over as long as it rotates, despite its inclination.
Especially in astronomy , precession means the change in direction of the earth's axis , which is a consequence of the mass attraction of the moon and the sun in connection with the deviation of the earth's shape from the spherical shape. It expresses itself through the progression of the vernal equinox along the ecliptic , from which the term precession ( Latin for 'progression') is derived.
Basics
If an attempt is made to tilt its axis of rotation on the rotating top , then there is a force effect perpendicular to the direction of tilt of the axis of rotation. The faster the top rotates, the greater the forces that occur . This can be explained by the high angular momentum of the top, which has to be changed in its direction. Its change takes place in the direction in which the axis of rotation is tilted and requires a torque that lies in the tilting plane. The torque to be applied determines the force effect perpendicular to the direction of tilt.
Assume a rotating table top that is inclined. Due to its mass, its weight acts on the center of gravity of the top and an equally large opposing force at the point of support. The resulting torque
tip over a non-rotating top. It indicates the angle between the axis of rotation and the force of gravity , r is the distance between the point of support and the center of gravity of the top, and m is the mass and g is the acceleration due to gravity .
It is known that lopsided tops sweep the characteristic precession cone with the cone axis along the force of gravity. Therefore, assume an angular velocity at which the axis of rotation of the gyro is pivoted and as a result of which the gyroscopic moment occurs. This angular velocity is now aligned along the force of gravity and should have an amount such that it cancels out the torque that causes the top to tilt. indicates the angular momentum of the top.
The gyroscopic moment lies in the plane perpendicular to gravity and points in the opposite direction to the torque that tilts the gyro. By converting the cross product into the amount notation, the amount of the gyroscopic torque results and can be equated with the torque from the weight force. The angular velocity of the precession movement follows from the gyro data by changing the position.
It turns I S , the moment of inertia is and ω S is the angular velocity of the gyro. The gyroscopic moment is an approximation formula for and so is the resulting formula.
The resulting change in angle over time is called the precession constant when the earth rotates .
The precession can be understood intuitively taking into account the square wheel model. Suppose we replace the tire of a spinning and precessing wheel (the top) suspended at one of the ends of its axis of rotation with the flow of an ideal, heavy and incompressible fluid with streamlines that are exactly parallel to the tire. In this way we can create the same angular momentum as with a spinning wheel, while the flow loop can be made into the shape of a square (or a slightly curved square). The absolute speed of the flow is higher in the lower square wheel segment than in the upper square wheel segment, since the speed of the precession and the flow add up in the lower segment, while they subtract in the upper segment. Therefore, the centripetal forces that keep the fluid on the curved trajectory have a larger value in the lower segment and a smaller value in the upper segment. The torque that "lets the top float" is created by the opposing forces of the centripetal forces.
Precession of the earth's axis
Principle and description
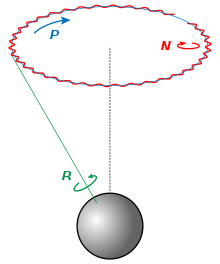
The earth does not have an exact spherical shape, but rather the shape of a flattened ellipsoid ( earth ellipsoid ) due to its rotation : The equatorial radius is around three hundredths or 21.4 km larger than the distance of the poles from the center of the earth . This equatorial bulge (English equatorial bulge effected) that the tidal forces of the moon and sun , a torque produce that is attempting to the Earth's axis and for precession of the axis of the earth leads ( lunisolar precession , marked in the drawing with P).
The earth's axis thereby completes a conical orbit around an axis that is at right angles to the plane of the ecliptic . The (almost) constant angle between the earth's axis and the axis of the cone is the skew of the ecliptic ; it is currently around 23.44 °. A full orbit of this precession movement of the earth's axis takes about 25,700 to 25,850 years. This period is called the cycle of precession (also called the Platonic year ) and is described by the precession constant .
The plane of the lunar orbit , which is inclined by around 5 ° in relation to the plane of the ecliptic, also exhibits a precession movement, i.e. H. its normal vector describes a cone orbit around the normal vector of the ecliptic. The resulting change in torque also has an effect on the change in direction of the earth's axis: The conical precession orbit is superimposed by a periodic deviation with an amplitude of 9.2 ″ and a period of 18.6 years. This nodding movement of the earth's axis is called nutation ; it is denoted by N in the drawing. There are also other nutation components with shorter periods and amplitudes below 1 ″. (The astronomical term nutation used here is not identical to the term nutation used in mechanics in gyro theory .)
Effects
Together with the conical orbit of the earth's axis, the plane of the equator , which is perpendicular to the earth's axis, also rotates . The straight line directed towards the vernal equinox , in which the equator and the ecliptic intersects at an angle of currently about 23.44 °, rotates clockwise on the ecliptic with the same period of around 25,800 years (when viewed from the direction of the northern pole ). Its angular velocity of 360 ° in 25,800 years or around 50 ″ per year is the precession constant .
Changeable star locations
The spring point or the equinox line determined by it is a reference axis for both the equatorial and the ecliptical coordinate system . As a result of the precession, the spatial orientations of these two coordinate systems and thus also the coordinates of the fixed stars related to the equatorial system change gradually . This effect has been known for over two thousand years. The Greek astronomer Hipparchus compared around 150 BC The star locations of his newly measured catalog with the data from several hundred years old records and determined differences. The Babylonians are likely to have discovered the phenomenon of precession about 170 years earlier than Hipparchus. However, it was not until the 16th century that Nicolaus Copernicus recognized the inclination of the earth's axis and its movement as the cause of the shift in the vernal equinox.
Definition of a year
The precession of the earth's axis also affects the definition of a year. Generally refers to less than one year during the period in which the circulating in the ecliptic straight going from the sun to the earth (or from the earth to the sun) its direction by 360 ° change ( against clockwise when viewed from the direction of the north pole) .
- In the sidereal year , this change in direction is related to a reference axis that does not move along the ecliptic.
- When tropical year is the reference axis, however, the vernal equinox, which due to the precession of the Earth's axis at an angular speed of 50 "per year in the shifting direction of the ecliptic.
Therefore, the angle to be covered for the straight line from the earth to the sun is somewhat smaller relative to the spring equinox, and thus a tropical year is somewhat shorter than a sidereal year.
Because the vernal equinox executes a 360 ° orbit within 25,800 years, the number of revolutions of the straight line from the earth to the sun relative to the vernal equinox is 1 greater than relative to a fixed reference axis. The difference between a tropical and a sidereal year adds up to a whole year in 25,800 years; consequently a tropical year is 25,800th of a year ≈ 20 minutes shorter than a sidereal year.
For the seasons on earth, it is not the direction of the sun in relation to an absolutely fixed coordinate system, but in relation to the equatorial coordinate system whose polar axis is the precessing earth axis; for example, the beginning of spring is always when the sun is in the direction of the spring equinox, regardless of the fact that it moves slowly. For this reason, the current leap year regulation defines the calendar year in such a way that it adapts well to the tropical year on a long-term average.
Different stars as a pole star
At the moment the earth's axis points very precisely in the direction of the North Star , so that all fixed stars seem to describe a circular path around it. As a result of the precession, the celestial pole is not fixed at the pole star, but moves around the ecliptic pole on a circle with a radius of about 23.5 ° ( skew of the ecliptic assumed to be constant) . In 12,000 years, the celestial pole will be located near Vega in the constellation Lyra , the second brightest northern star, and the constellation “ Big Dog ”, for example, will no longer be visible from Central Europe, from the constellation Orion only the shoulder stars .
Influence on the cold ages?
In the context of the Milanković cycles there is an influence of precession on the ice ages , but the extent of this is still unclear.
See also
Individual evidence
- ^ Péter Hantz, Zsolt I. Lázár: Precession intuitively explained . In: Frontiers in Physics . 7, 2019. doi : 10.3389 / fphy.2019.00005 .
- ↑ Nicolaus Copernicus: De revolutionibus orbium coelestium , 3rd book, chapter 1
Web links
- Precession of the earth's axis in the astronomy library on Astronomie.de
- Precession of a rotating wheel suspended laterally from its center of gravity
- Animated Java simulation of the one-sided supported gyro with all parameters (initial conditions, precession, nutation, friction at the contact point, friction in the gyro axis)
- Video: precession of a rotating wheel . Institute for Scientific Film (IWF) 2003, made available by the Technical Information Library (TIB), doi : 10.3203 / IWF / C-14828 .