
flattened ellipsoid of revolution
|

elongated ellipsoid of revolution
|
A rotational ellipsoid (English spheroid ) is a surface of revolution that is created by rotating an ellipse around one of its axes. In contrast to a three-axis or triaxial ellipsoid , two axes are of the same length.
Depending on which of the two semi-axes of the generating ellipse acts as the axis of rotation , a distinction is made:
Occurrence

Ellipsoid of revolution and mass displacement (red)
Most of the larger celestial bodies are approximately flattened ellipsoids of revolution, which are also called spheroids . They are caused by centrifugal force , which causes a rotating spherical body to be deformed. These bodies are flattened at the poles , i.e. the intersection points of the axis of rotation , and a bulge arises at the equator . The flattening of the large gas planets Jupiter and Saturn is particularly pronounced because they rotate particularly quickly and are not solidified. But the earth and the other planets of the solar system are also deformed into ellipsoids of rotation by the centrifugal forces generated during rotation. Jupiter, which rotates in ten hours, is flattened by about 1/16, the flattening of the earth is 1 / 298.257223563 ( WGS 84 ).
Elliptical galaxies are often not spheroids, but triaxial.
Parametric representation
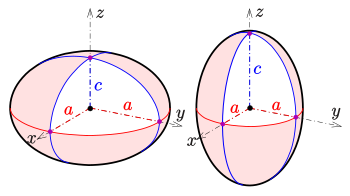
flattened and elongated ellipsoid of revolution
The following parameter representation describes an ellipsoid of revolution, which by rotation of the half- ellipse (in the - - level ) to the created axis (s. Surface of revolution ):




-
 .
.
The numbers are the semi-axes of the rotating semi-ellipse. In the case , a flattened ellipsoid of revolution arises, in the case of an elongated ellipsoid of revolution. If is, a sphere with a radius results .





Note: The poles (points on the axis of rotation ) do not have a clear representation.
The resulting ellipsoid of revolution has the implicit representation :

volume
The volume of the above ellipsoid of revolution is
-
 .
.
Here is the radius of the equatorial circle and the distance between the poles and the center .


surface
The surface for the flattened ellipsoid ( ) is also calculated


that of the elongated ellipsoid ( ) with


A sphere with a radius has the volume and the surface (see sphere).



- Derivation of the formulas
The content of the surface of a shell by rotating the curve generated surface of revolution is

-
 (see surface of revolution )
(see surface of revolution )
For the above ellipsoid of revolution is . So it has to be the integral

(2 times half an ellipsoid) can be calculated. For is and it results in the surface of a sphere . The following is assumed.



The substitution with leads to



and thus to
-
 if , and
if , and
-
 if .
if .
Taking into account that the fraction below the square root is positive in both cases, the antiderivatives for the two integrals and finally the formulas given above for the surface result from an integration table (e.g. Bronstein-Semendjajew ) .
application
In geodesy , cartography and the other geosciences , ellipsoids of revolution are used as a geometric approximation of the physical geoid . These ellipsoids of revolution then serve as a reference surface to indicate the position or height of objects on the earth's surface . One then speaks of a reference ellipsoid .
In a hollow body, the boundary surfaces of the (stretched) ellipsoid of revolution reflect the radiation from one focal point to the other. A whisper vault uses the effect to bundle sound waves .
Thus formed optical reflectors focus the radiation from a nearly point-shaped, in one of the focal points located light source on the other focus of the ellipsoid . The interface of a fiber optic cable , another optical element or the location of a radiation-induced process can be located there.
Application examples
Jupiter and Saturn
The planets Jupiter and Saturn are much flatter at the poles than at the equator due to the centrifugal forces acting due to the rapid rotation and have approximately the shape of an ellipsoid of revolution.
Jupiter
Jupiter has an equatorial diameter of 142,984 km and a pole diameter of 133,708 km. So for the semi-axes and . The mass of Jupiter is about 1.899 · 10 27 kg. Using the above formulas for volume , mean density and surface, this results in :


-
Volume :

- That is about 1,321 times the volume of the earth.
-
Medium density :

- Overall, Jupiter has a slightly higher density than water under standard conditions .
-
Surface :

- That's about 121 times the surface of the earth.
Saturn
Saturn has an equatorial diameter of 120,536 km and a pole diameter of 108,728 km. So for the semi-axes and . The mass of Saturn is about 5.683 · 10 26 kg. This results in:


-
Volume :

- That's about 764 times the volume of the earth.
-
Medium density :

- Overall, Saturn has a slightly lower density than water under standard conditions .
-
Surface :

- That's about 84 times as much as the surface of the earth.
Rugby ball
A rugby ball is around 280 millimeters long and has a diameter of around 200 millimeters on the minor axis . So for the semi-axes and . The mass of a rugby ball is around 400 grams. This results in:


-
Volume :

-
Medium density :

In contrast to golf balls, rugby balls float on the water.
See also
Web links
Individual evidence
-
↑ Beyer, CRC Handbook of Mathematical Sciences, 5th Edition, p. 198.














































