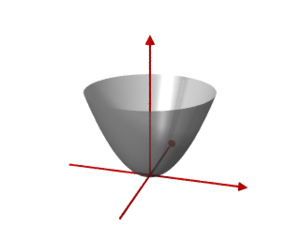
Paraboloid of revolution

A rotated parabola results in a paraboloid of revolution

In mathematics, a paraboloid of revolution is a surface of revolution that is created by rotating a parabola around its axis of symmetry .

Examples from everyday life are reflectors for headlights or parabolic mirrors in astronomy .

If you rotate a liquid evenly around a vertical axis , gravity and centrifugal force are superimposed and the liquid surface takes on the shape of a paraboloid of revolution. This is how the mercury telescope works . In this way you can also cast parabolic mirrors for mirror telescopes so that you don't have to grind off as much material afterwards, since the surface obtained during casting already represents a paraboloid of revolution.

For the use of paraboloids of revolution as mirrors, see the article on so-called parabolic mirrors .

The paraboloid of revolution is the rotationally symmetrical special case of the elliptical paraboloid .

Mathematical representation

The formulas apply to a paraboloid of revolution, which is cut off in height from a plane perpendicular to the z-axis and has the radius there. ${\ displaystyle h}$ ${\ displaystyle r}$

equation: ${\ displaystyle z = {\ frac {h} {r ^ {2}}} (x ^ {2} + y ^ {2}) \, 0 \ leq z \ leq h \}$
Focus (see parabola ): ${\ displaystyle (0,0, {\ frac {r ^ {2}} {4h}})}$
volume: ${\ displaystyle V = {\ frac {\ pi} {2}} \ cdot r ^ {2} \ cdot h}$
Surface (without covering circle surface): ${\ displaystyle A_ {O} = {\ frac {\ pi r} {6h ^ {2}}} \ cdot \ left [\ left (r ^ {2} + 4h ^ {2} \ right) ^ {\ frac {3} {2}} - r ^ {3} \ right]}$