volume
| Physical size | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Surname |
Volume volume |
||||||||||||
| Formula symbol | |||||||||||||
| Derived from | length | ||||||||||||
|
|||||||||||||
The volume ( Pl. Volume or volumes ; from Latin volume “winding, curvature”, from volvere “rolling, rolling”), also: space or cubic content , is the spatial content of a geometric body . Common symbols is V .
In physics , volume is the extension (the space required ) of a body. The (coherent) SI unit for the spatial dimension is the cubic meter ( unit symbol m 3 ). Occasionally you can still read the outdated abbreviations cbm for m³ and ccm for cm³. The unit liter is common for gases and liquids and is defined as 1 dm 3 (10 × 10 × 10 cm³).
Technically, a distinction must be made:
- Hollow volume , the free space within certain limits, such as the capacity of a container
- Volume , the volume of solids , of liquids or gases
history
The first known formulas for determining volume (including stereometry ) come from early Egypt . The Moscow Papyrus is a collection of arithmetic problems and dates from around 1850 BC. Chr. Dated. Among other things, the formulas for determining the volumes for rectangular cones are described here. The determination was achieved through analysis and subsequent synthesis . That is, the body was broken down into several known bodies and the individual volumes added.
Measurement methods
In the course of time, very different methods for determining volumes have developed:
- Gauging : the body is filled with sand or water , the amount of which is then determined in a known vessel; thus the volume of their interior can be determined in the case of vessels.
- Water displacement : the body is immersed in a vessel completely filled with water. The volume of the overflowing water is then measured in a geometrically simple vessel (e.g. cylinder ). As a result of possible interactions between test specimen and water, measurement errors can occur, which is why other liquids can also be used.
- For a body with a known density , the volume can also be weighed .
Volume calculation
Mathematically speaking, the volume (the volume of space) is a measure of a measurable subset of ordinary three-dimensional space. In general, the volume of a body (area in ) can be described by a 3-fold integral . Such integrals can be very difficult or only numerically solvable. In many simple cases (polyhedra) the volume can be determined without integrals. For solids of revolution and those with continuous cross-sectional areas (see table), simple integrals are sufficient. Here are the volumes of some common bodies:
| body | volume | parameter |
|---|---|---|
| cube |
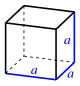
|
|
| Cuboid |

|
|
|
prism (Base G ) |

|
|
|
pyramid (Base G ) |
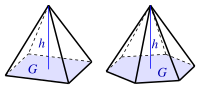
|
|
| Bullet |

|
|
| Ellipsoid |

|
|
| vertical circular cylinder |

|
|
| vertical circular cone |
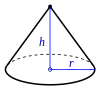
|
|
| Torus |

|
|
| Body of revolution |

|
|
| Body with steady
Cross-sectional area
(e.g. Steinmetz body )
|
For the solid of revolution is
|
generalization
A volume can also be defined using multidimensional manifolds, see also Volume Form . According to this generalization, the volume of a subspace of the two-dimensional Euclidean space is its area, and the same applies to higher-dimensional Euclidean spaces. For example, an n-dimensional hypercube with edge length has a volume of .
The volume of an orientable Riemann manifold is defined by integrating the volume form over the manifold.
cavity
A cavity is a mathematical, physical, or natural object. A cavity has a volume called a void volume. A volume enclosed in a structure can be a cavity. The existence of cavities often changes the surrounding structure, e.g. B. in terms of strength or elasticity (see porosity ).
A natural cavity contains a vacuum or is filled with gases, liquids or other substances, which in turn can influence the surrounding structure. In particular, the interface between the cavity and the structure can change, be difficult to recognize or only exist on a conceptual level. A cavity that has one or more openings, that is, is not completely surrounded by the surrounding structure, is colloquially referred to as this.
The size of the enclosed volume can often be calculated or determined experimentally. In some cases, however, this is not possible in principle.
Cavitation is a common phenomenon in geological and other physical and chemical processes.
Evacuated cavities have several universal properties, one of which is cavity radiation .
Examples: cavity
- ... as a vessel: bottle , tank , digestive system, sponge
- ... as a place to stay: apartment, cave
- ... as the result of chemical or physical processes: air bubbles, soap bubbles, "holes" in the cheese, blowholes
See also
- Banach-Tarski Paradox and Measure Theory , on the limits of the concept of volume in mathematics when used in the real world
- Order of magnitude (volume)
Web links
- Edmund Hlawka: On the history of the concept of content
Individual evidence
- ↑ cubic content. In: Digital dictionary of the German language . Retrieved September 6, 2019
- ↑ There are also subsets for which no volume can be determined, which means that they cannot be measured. See z. B. Vitali's theorem (measure theory) .



















