
Straight circular cone (left) and oblique circular cone
A cone or cone is a geometric body that is created when all points of a bounded and connected area lying in a plane are connected in a straight line with a point (tip or apex) outside the plane. If the patch is a circular disk , the body is called a circular cone . The area is called the base area, its boundary line is the guide curve and the point is the apex or apex of the cone. A cone thus has a point (the apex), an edge (the guide curve) and two surfaces (the surface and the base).
The height of the cone means, on the one hand, the perpendicular from the tip to the base (the height is always perpendicular to the base), and on the other hand, the length of this perpendicular (i.e. the distance between the tip and the base).
The connecting lines of the tip with the guide curve are called surface lines, their union forms the cone surface or the surface.
Straight and oblique cone
When speaking of a cone in geometry , the special case of the straight circular cone is often meant. A circular cone is a body that is defined by a circle ( base circle or base circle ) and a point outside the plane of the circle ( tip of the cone).
The plane in which the base circle lies is called the base (circle) plane. The radius of the cone is usually understood to be the radius of the base circle. The straight line through the center of the base circle and the tip is called the axis of the cone. The height of the cone is the distance of the apex from the base plane; this distance must be measured perpendicular to the base plane.


If the axis is perpendicular to the base plane, there is a straight circular cone or a rotating cone . Otherwise one speaks of an oblique circular cone or elliptical cone. Each elliptical cone has two directions in which its intersection with a plane is a circle; this fact makes use of the stereographic projection as a true circle .
The term "rotary cone" indicates that it is a solid of revolution. It is created by rotating a right triangle around one of its two legs . In this case, the surface lines (in other words, the links of the (edge) points of the base circle with the tip) also called generators ( as it will make), coat "Create". The opening angle is twice the angle between the surface lines and the axis of a rotary cone. The angle between the surface lines and the axis is called half the opening angle.

A rotary cone with an opening angle of 60 ° is called an equilateral cone. This designation is explained as follows: If you intersect such a cone with a plane that contains the axis, you get an equilateral triangle.
The word cone (from Latin conus ) is also used for the rotary cone, especially in technology . The associated adjective conical designates objects with the shape of a cone of rotation or a truncated cone .
In connection with conic sections in particular , the word “cone” is also used in the sense of the double cone mentioned below .
Quantities and formulas
| Quantities and formulas
|
radius
of a straight circular cone
|

|
height
of a straight circular cone
|

|
Surface line
of a straight circular cone
|

|
angle 
a right circular cone
is half the opening angle,
also half cone angle mentioned
|
Application of the trigonometric functions



|
Diameter of the base
of a straight circular cone
|

|
Floor space
of a circular cone
|

|
Area of the lateral surface
of a straight circular cone
|

|
surface
of a straight circular cone
|

|
volume
of any circular cone
|

|
Moment of inertia
The axis of rotation runs through the tip
and through the center of the base.
|
of a rotating, massive and straight circular cone:

of the rotating mantle of a right circular cone:
where is the density and the mass .

 
|
proofs
volume
Already in 1781 Johann Friedrich Lorenz describes in his translation Euclid's elements Euclid's statement: Every cone is the third part of a cylinder, which with it has a base area, ABCD, and the same height. In elementary geometry , the volume formula is often based on the Cavalieri principle . One compares the given circular cone with a pyramid of the same base area and height. For planes parallel to the base area at any distance, it follows from the laws of similarity or centric extension that the corresponding cut surfaces have the same area. Therefore, the two bodies must match in volume. The volume formula valid
for pyramids of base and height


can therefore be transferred to the cone. Together with the formula for the circular area one obtains
-
 .
.
It is also possible to approximate the cone using a pyramid with a regular n-gon as the base area (for ).

Another proof (shown here especially for the straight circular cone) uses the integral calculus as an aid. A Cartesian coordinate system is used, with the tip of the cone at the origin (0 | 0) and the center of the base circle at the point ( | 0). The cone can now be thought of as composed of an infinite number of cylindrical disks of infinitesimal (infinitely smaller) height (thickness) . Since the distance between such a cylindrical disk and the tip of the cone is given by the coordinate , the following applies according to the ray theorem :



- Radius of an infinitesimal cylinder:

- Volume of an infinitesimal cylinder:

The total volume of the rotary cone corresponds to the totality of all these infinitely small cylinders. For the calculation one forms the definite integral with the integration limits 0 and :


![{\ displaystyle V = {\ frac {r ^ {2} \ pi} {h ^ {2}}} \ left [{\ frac {x ^ {3}} {3}} \ right] _ {0} ^ {H}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2138a85318cfab70e0cc2887ec38da21627a4b73)


This leads to the familiar formula
-
 .
.
Outer surface

Straight circular cone with a developed lateral surface
The lateral surface of a right circular cone is curved, but at a circular sector unwound . The radius of this sector corresponds to the length of a surface line of the cone ( ). The center angle of the circle sector can be determined by a ratio equation. It is related to the 360 ° angle like the arc length (circumference of the base circle) to the entire circumference of a circle with a radius :





The area of the lateral surface you are looking for results from the formula for the area of a sector of a circle:

The development of the lateral surface of a straight circular cone is carried out approximately with compasses and ruler in the descriptive geometry: s. Development (descriptive geometry) .
Center angle α
The center angle can be based on the formula


be calculated:

as well

with = base diameter, = surface line = character radius.


Double cone

Double cone with points pointing towards each other, similar to an
hourglass
A double cone is created as the surface of revolution of a straight line around an axis that does not intersect at right angles . There are two cones of rotation with the same opening angle and a common axis that touch at the tip. If you cut such an infinite double cone with a plane, the conic sections are created : circle , ellipse , parabola , hyperbola .
Analytical description
A perpendicular circular cone (double cone) with the tip at the origin and the z-axis as the axis of symmetry can be expressed by an equation

describe. The number is the radius of the height circles of the heights . Is , the equation simplifies to




and in this case the cone is called the unit cone (analogous to the unit circle).
Just as any ellipse is the affine image of the unit circle , any cone (as a quadric ) is the affine image of the unit cone . The simplest affine mappings are scaling of the coordinates. Scaling the x and y axes results in cones with equations

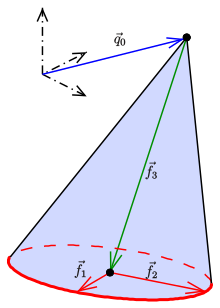
Vectors for the parametric representation of a general cone (quadric)
The vertical sections of such cones are ellipses. The intersection with the elevation plane is the ellipse . The cone is equal to the union of all straight lines (generators) through the apex and the points of the ellipse. If you describe the ellipse using the parametric representation and represent the generators in parametric form, you get the following parametric representation of the cone :






The equation of a cone positioned anywhere in space is difficult to give. The parametric representation of any cone, on the other hand, is relatively simple:

Here is the tip of the cone and are three linearly independent vectors. points in the direction of the cone axis (see picture). For every constant parameter there is an ellipse with which one can imagine (together with the tip) the cone being generated.




If the three vectors are orthogonal in pairs and is , then the parametric representation describes a perpendicular circular cone.


That any elliptical cone always contains circles is shown in the circular section plane.
Cone coordinates (coordinate transformation)
Parametric representation
The parameter representation of the cone can be described as follows. With the illustration , the cone coordinates can be converted into Cartesian coordinates. With the illustration , the Cartesian coordinates can be converted into cone coordinates.



Conversion of a given cone segment into cone coordinates

Conical segment with height h and the radii r1 and r2
The parameters of a cone segment are given by (see adjacent figure):
-
 ,
,
Then the limits can be expressed in cone parameters as follows:
-
 .
.
The parameters of a solid cone segment are in the range:
-
 .
.
The following parameter representation applies to the corresponding lateral surface of this conical segment:
-
 .
.
The surface normal vector is orthogonal to the lateral surface of the cone. It is required to B. perform flow calculations through the surface area. The area of the lateral surface can be calculated as a double integral using the norm of the surface normal vector.

Unit vectors of the cone coordinates in Cartesian components
The unit vectors in Cartesian components are obtained by normalizing the tangent vectors of the parameterization. The tangent vector results from the first partial derivative according to the respective variable. These three unit vectors form a normal basis. This is not an orthonormal basis because not all unit vectors are orthogonal to one another.

Transformation matrices
The functional matrix and its inverse are needed to transform the partial derivatives later.


The transformation matrix is required to transform the unit vectors and vector fields. The matrix is composed of the unit vectors of the parameterization as column vectors. More details can be found under the article change of base .

The partial derivatives can be transformed with the inverse Jacobi matrix.

The result is:



The unit vectors can be transformed with the inverse transformation matrix.

The result is:



Transformation of vector fields
Vector fields can be transformed by matrix multiplication with the transformation matrix.

The result is:



Surface and volume differential
The volume differential can be specified using the determinant of the Jacobi matrix. This offers the possibility, for. B. to calculate the volume of a cone using a three-fold integral.

The surface differential can be specified with the norm of the surface normal vector. So you can z. B. determine the area of the lateral surface using a double integral.

Transformed vector differential operators
Nabla operator
A representation of the Nabla operator in cone coordinates can be obtained by inserting the transformed unit vectors and partial derivatives into the Cartesian Nabla operator:

gradient
The gradient in cone coordinates is obtained by applying the transformed Nabla operator to a scalar field in cone coordinates.

divergence
The operator for the divergence of a vector field is obtained by applying the Nabla operator to the vector field in conical coordinates:

Laplace operator
The Laplace operator is the divergence of a gradient. In cone coordinates this gives the following operator:


rotation
The rotation of a vector field can be understood as the cross product of the Nabla operator with the elements of the vector field:

Generalizations
- Convex sets
The property of the (infinite) cone, consisting of rays with a common starting point, is generalized to conical sets, to which z. B. also belongs to an infinitely high pyramid . The convex cones that play a role in linear optimization are of particular interest .
The concept of the order cone is important: If one defines a half-order by means of , where a convex and closed cone is, then this is reflexive, antisymmetric, transitive and multiplicative as well as additively compatible. Such a partial order is thus a generalization of the (component-wise) arithmetic partial order on which the positive orthant is based. One possible definition of such a cone is:



Let be a real Banach space and a non-empty subset of . is called a cone if the following conditions are met:




-
 is closed,
is closed,
-
 ,
,
-
 ,
,
-
 .
.
If the fourth condition is omitted, a possible definition of a wedge is obtained .
More general areas
- topology
In topology , the cone over a topological space is understood as the space that is obtained from the product by identifying all points in (the “cone tip”).

![X \ times [0.1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd76f8aa27cdb748a869ec11fc6548bcab6d396b)

The corresponding "double cone" (through the additional identification of ) is also known as a suspension or suspension.
Application examples
Drinking glass
Some drinking glasses , for example a martini glass , have approximately the shape of a cone.
A martini glass with a diameter of 103 millimeters and a filling height of 59 millimeters is filled to the brim with orange juice . This gives the volume and the surface area :
-
Volume :

-
Outer surface :

The martini glass can therefore be filled with about 164 milliliters of orange juice . The outer surface is approximately 127 square centimeters .
See also
literature
- Rolf Baumann: Geometry for the 9./10. Class . Centric stretching, Pythagorean theorem, circle and body calculations. 4th edition. Mentor-Verlag, Munich 2003, ISBN 3-580-63635-9 .
Web links
Individual evidence
-
^ Johann Friedrich Lorenz: Euclid's elements, fifteen books, translated from the Greek . Ed .: In the publishing house of the bookstore des Waysenhauses. Twelfth book. Hall 1781, S. 308 ff . ( The 10th sentence. Each cone is the third part of a cylinder, ... [accessed November 1, 2018]).
-
↑ E. Hartmann: Computer-assisted performing and constructive geometry. Darmstadt University (PDF; 3.4 MB), p. 105.

































![{\ displaystyle V = {\ frac {r ^ {2} \ pi} {h ^ {2}}} \ left [{\ frac {x ^ {3}} {3}} \ right] _ {0} ^ {H}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2138a85318cfab70e0cc2887ec38da21627a4b73)






































































![X \ times [0.1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd76f8aa27cdb748a869ec11fc6548bcab6d396b)



