Stereographic projection

A stereographic projection (also conformal azimuthal projection ) is an image of a spherical surface in a plane with the help of a central projection, whose projection center (PZ) lies on the sphere. The straight line containing the projection center and the center of the sphere is orthogonal to the image plane, which is traditionally the tangential plane lying opposite the projection center .

The stereographic projection was first used to depict the celestial sphere on the astrolabe . It was discovered in antiquity, probably by Hipparchus around 130 BC. It is detailed in the small treatise Planisphaerium of Ptolemyos (approx. 85-160) presented in detail and with geometrical proof that circles on the spherical surface merge into circles of the image plane ( circular fidelity ) . The Nuremberg astronomer and mathematician Johannes Werner (1468–1528) first came up with the idea of using the circular and angular accuracy of this image for cartographic images of the earth's surface .

In the Crystallography the stereographic projection finds practical application in view of the lattice planes of a crystal (usually angle-preserving means of the so-called Wulff'schen network ) and in the structural geology in the representation of terrain data as the strike and falling of layer -, foliation -, discard - and gap areas (usually equal to area using the so-called Schmidt network ).

In pure mathematics , the stereographic projection has an expanded, more abstract meaning. It is also used for higher-dimensional spaces, i.e. not just for mapping from three-dimensional into two-dimensional space.

Figure 1: Stereographic projection of the lower half of a sphere surface and a great circle inclined to the image plane (red, e.g. the ecliptic on the celestial sphere from a celestial pole )

Application examples

Image 2: Rotatable star map (here in the azimuthal projection that is mostly used today and has a similar result ). The name " PLANISPHERE " was adopted from the astrolabe .

Image 1: Stereographic projection of the northern starry sky on an astrolabe

Image 4: If the image plane is on the equator , the meridians and the parallels are shown as circles. The highlighted area of ​​the circle is half of the earth's surface.

Image 3: If the image plane is on the Earth's pole , the meridians are shown as straight lines and the circles of latitude as concentric circles around the pole. The highlighted content of the circle is half of the earth's surface, it ends at the equator .

Astrolabe and star map

The astrolabe in picture 1 contains the northern sky. The projected stars (including the zodiac) are located on the Rete, which can be rotated around the image of the northern celestial pole ( Pole Star ) . The safiha is engraved on the solid base ( tympanum ), which consists of the images of the horizontal circles ( almucantarates ) concentric to the zenith , the horizon (image: a concave line) and the azimuth circles at right angles to it .

A star map similar to the rotatable Planisphere shown in Figure 2 is the useful, but cheaper follow-up product of the astrolabe, which in principle works in the same way. The interrupted circular arc is the ecliptic , a piece of an eccentric circle in the illustration of the polar pattern.

Cartography of the earth's surface

The easy drawing production (only circles and straight lines for circles on the earth's surface) and the angular accuracy were also used in ancient times for maps and for navigation. If the point of contact of the mapping plane is placed in a port city, for example, the shortest routes to destinations are shown as straight lines in all directions.

With the polar stereographic projection (the point of contact of the image plane is in the north or south pole), the meridians of the earth's geographic coordinate system are mapped as straight lines through the earth's pole (see Figure 3). The navigation elements geographical longitude and geographical latitude are therefore clearly displayed by this type of projection for navigation purposes at the poles. The depiction of the earth's poles as parts of the modern international world map is also carried out via stereographic projection.

In geophysics , maps of the distribution of forces or line structures on the globe are built on a stereographic network design.

Mathematical treatment

Conversion of image to object coordinates

Figure 3: Stereographic projection of a sphere (half): projection of parallel circles of equal central angle distance and of meridian circles

Figure 2: Spherical coordinates of the point on the sphere ${\displaystyle r,\theta ,\varphi }$ ${\displaystyle P}$

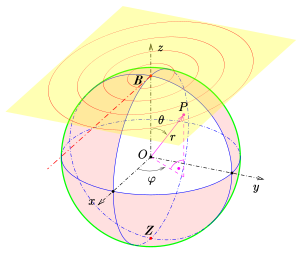
Spherical ( as in Figure 2) and plane polar coordinates (radius , direction , as in Figure 3) are used for the object points . ${\displaystyle r,\theta ,\varphi }$ ${\displaystyle m}$ ${\displaystyle \alpha }$

An object point is mapped onto the image point . ${\displaystyle P:=(r,\varphi ,\theta )}$ ${\displaystyle P':=(\alpha ,m)}$

The same reference direction is assumed for the angles and . Thus: ${\displaystyle \varphi }$ ${\displaystyle \alpha }$

${\displaystyle \alpha =\varphi }$

The distance (radial polar coordinate) can be seen from triangular observations (see Figure 3): ${\displaystyle m}$

${\displaystyle m=2\cdot r\cdot \tan {\frac {\theta }{2}}}$

While the length of the arc on the sphere increases linearly from the point of contact to the circle of latitude, the radius in the plane increases progressively to infinity (up to the projection center). This so-called length distortion is the differential quotient of the normalized function according to : ${\displaystyle m}$ ${\displaystyle h}$ ${\displaystyle r}$ ${\displaystyle {\frac {m}{r}}}$ ${\displaystyle \theta }$

${\displaystyle h={\frac {d}{d\theta }}\left({\frac {m}{r}}\right)={\frac {d}{d\theta }}\left(2\cdot \tan {\frac {\theta }{2}}\right)={\frac {1}{\cos ^{2}\theta /2}}}$

Because of the strongly progressive increase in the distortion (infinitely large at ) the stereographic images remain limited in practice . ${\displaystyle \theta =180^{\circ }}$ ${\displaystyle \theta \leq 90^{\circ }}$

${\displaystyle \theta }$ ${\displaystyle m/r}$ ${\displaystyle h}$ 00 ° 00 ° 1 05 ° 05.003 ° 1.002 10 ° 10.025 ° 1.008 15 ° 15.086 ° 1.017 20 ° 20.206 ° 1.031 25 ° 25.404 ° 1.049 30 ° 30.705 ° 1.072 35 ° 36.131 ° 1,099 40 ° 41.708 ° 1,132

${\displaystyle \theta }$ ${\displaystyle m/r}$ ${\displaystyle h}$ 45 ° 47.47 ° 1.17 50 ° 53.43 ° 1.22 55 ° 59.65 ° 1.27 60 ° 66.16 ° 1.33 65 ° 73.00 ° 1.41 70 ° 80.24 ° 1.49 75 ° 87.93 ° 1.59 80 ° 96.15 ° 1.7 85 ° 105.0 ° 1.84

${\displaystyle \theta }$ ${\displaystyle m/r}$ ${\displaystyle h}$ 90 ° 114.6 ° 2 100 ° 136.6 ° 2.4 110 ° 163.7 ° 3.0 120 ° 198.5 ° 4th 130 ° 245.7 ° 5.6 140 ° 314.8 ° 8.5 150 ° 427.7 ° 14.9 160 ° 649.9 ° 33.2 170 ° 1310, ° 131,

Geographical coordinates of the earth

If you want to depict the northern hemisphere stereographically, the following assignments result:

• The projection center coincides with the south pole, the point of contact with the north pole.
• ${\displaystyle \Theta =\pi /2-\delta }$
• ${\displaystyle \varphi =\lambda }$

In this way, the latitudes appear in the projection plane as concentric circles around the point of contact (= north pole) and the longitudes as semi- straight lines of origin .

The following applies to the southern hemisphere:

• The projection center coincides with the North Pole, the point of contact with the South Pole.
• ${\displaystyle \Theta =\pi /2+\delta }$
• ${\displaystyle \varphi =-\lambda }$

Geometry of plane curves

Let any curve in the plane be given in explicit polar coordinate representation . Now place the projection sphere with radius on the origin of coordinates, the tangential point TP. Through the projection center - the opposite point PZ on the spherical surface - a second plane is now laid, which is parallel to the original plane (i.e. it is created by parallel displacement of the first plane perpendicular to the same ). Now the given curve in the first plane is projected onto the sphere by means of stereographic projection in PZ. By using the original point TP as the new projection center, the curve on the sphere is projected onto the second plane by means of a further stereographic projection - it is described there in polar coordinates by . Then applies . The given curve has thus been inverted by this double stereographic projection on the circle with radius in the (parallel) image plane . ${\displaystyle r(\varphi )}$ ${\displaystyle R}$ ${\displaystyle 2R}$ ${\displaystyle \rho (\varphi )}$ ${\displaystyle \rho (\varphi )={\tfrac {4R^{2}}{r(\varphi )}}}$ ${\displaystyle 2R}$

District loyalty

Figure 4: Proof of loyalty to the district

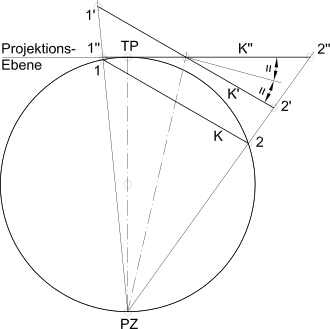
The rays from the projection center PZ (Fig.) To the original circle K (diameter points 1 and 2) form an oblique circular cone , the section K 'of which, parallel to K, is circular. The projection plane K ″ intersects the cone axis at the same angle as the section K ′, which is why the sectional figure lying in it is also a circle (points 1 ″ and 2 ″).
Important: The circle fidelity generally only applies to the circle line. The center of the object circle is z. B. not shown as the center of the image circle. Only the cases in which the circular cone is straight are excluded from this.

Other special features of stereographic projection are:

• The image of the projection center lies in infinity.
• All circles on the spherical surface are mapped as circles (circle fidelity).
  • Circles through the center of the projection are shown as straight lines.

Spherical reflection (inversion)

A stereographic projection can also be interpreted as a reflection on a sphere (inversion) . From the properties of an inversion, the true to the circle and true to angle then immediately follow.

Generalization to ℝ ⁿ

The projection described above is the special case of general stereographic projection: In three-dimensional space , the two-dimensional spherical surface is mapped onto the map plane and thus into two-dimensional space . The general illustration looks like this: ${\displaystyle \mathbb {R} ^{3}}$ ${\displaystyle S_{1}^{2}\left((0,0,1)\right)}$ ${\displaystyle \mathbb {R} ^{2}}$

${\displaystyle \sigma \colon \mathbb {R} ^{n+1}\supset S_{1}^{n}\left((0,\ldots ,0,1)\right)\backslash \{\left(0,\ldots ,0,2\right)\}\to \mathbb {R} ^{n}}$

${\displaystyle \sigma \left(x_{1},x_{2},\ldots ,x_{n+1}\right)=\left({\frac {2x_{1}}{2-x_{n+1}}},{\frac {2x_{2}}{2-x_{n+1}}},\ldots ,{\frac {2x_{n}}{2-x_{n+1}}}\right)}$

However, it is also possible to choose the archetype of this function so that its equator intersects the projection hyperplane :

Figure 5: In this variant of the stereographic projection, the sphere does not lie on the (hyper) plane, but intersects it.

${\displaystyle P_{N}\colon \mathbb {R} ^{n+1}\supset \mathbb {S} ^{n}\backslash \{\left(0,\ldots ,0,1\right)\}\to \mathbb {R} ^{n}}$

${\displaystyle P_{N}\left(x_{1},x_{2},\ldots ,x_{n+1}\right)=\left({\frac {x_{1}}{1-x_{n+1}}},{\frac {x_{2}}{1-x_{n+1}}},\ldots ,{\frac {x_{n}}{1-x_{n+1}}}\right)}$

This mapping is of course not defined for the point , the so-called North Pole. If you look at the figure , whose function term has instead of in the denominator, then the sphere is mapped to the south pole. ${\displaystyle N:=(0,\ldots ,0,1)\in \mathbb {R} ^{n+1}}$ ${\displaystyle P_{S}}$ ${\displaystyle x_{n+1}+1}$ ${\displaystyle 1-x_{n+1}}$

If the archetype of the stereographic projection is changed in this way, the two images and an atlas of the n-sphere are obtained. ${\displaystyle P_{S}}$ ${\displaystyle P_{N}}$

Derivation

The stereographic projection through the North Pole is derived here as an example. The same derivation can be used for the projection through the South Pole. The stereographic projection through the North Pole is intended to map a point of the sphere onto its image point in the hyperplane so that the image point lies on the straight line through the North Pole and . ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle \{x\in \mathbb {R} ^{n+1}\colon x_{n+1}=0\}}$ ${\displaystyle y}$ ${\displaystyle x}$

This straight line can go through

${\displaystyle g(t):=tN+(1-t)x=\left((1-t)x_{1},\ldots ,(1-t)x_{n+1}+t\right)}$

can be parameterized. This straight line intersects the plane , where: ${\displaystyle \{x\in \mathbb {R} ^{n+1}\colon x_{n+1}=0\}}$

${\displaystyle (1-t)x_{n+1}+t=0\Leftrightarrow (1-x_{n+1})t+x_{n+1}=0\Leftrightarrow 1-t=1+{\frac {x_{n+1}}{1-x_{n+1}}}={\frac {1}{1-x_{n+1}}}}$

It follows that the coordinates of the intersection of and through ${\displaystyle g(t)}$ ${\displaystyle \{x\in \mathbb {R} ^{n+1}\colon x_{n+1}=0\}}$

${\displaystyle \left({\frac {x_{1}}{1-x_{n+1}}},{\frac {x_{2}}{1-x_{n+1}}},\ldots ,{\frac {x_{n}}{1-x_{n+1}}},0\right)}$

given are. If we now consider the plane as , we get the stereographic projection through the North Pole. ${\displaystyle \{x\in \mathbb {R} ^{n+1}\colon x_{n+1}=0\}}$ ${\displaystyle \mathbb {R} ^{n}}$

Inverse functions

In addition to the stereographic projections through the north and south poles, there are through

${\displaystyle P_{N}^{-1}(y_{1},\ldots ,y_{n})=\left({\frac {2y_{1}}{\|y\|^{2}+1}},{\frac {2y_{2}}{\|y\|^{2}+1}},\ldots ,{\frac {2y_{n}}{\|y\|^{2}+1}},{\frac {\|y\|^{2}-1}{\|y\|^{2}+1}}\right)}$

${\displaystyle P_{S}^{-1}(y_{1},\ldots ,y_{n})=\left({\frac {2y_{1}}{\|y\|^{2}+1}},{\frac {2y_{2}}{\|y\|^{2}+1}},\ldots ,{\frac {2y_{n}}{\|y\|^{2}+1}},{\frac {1-\|y\|^{2}}{\|y\|^{2}+1}}\right)}$

continuous inverse functions described . Hence, and are homeomorphisms . A possible atlas has been found with the projection from the North Pole and that from the South Pole . This shows that the -sphere is a -dimensional topological manifold . ${\displaystyle P_{N}}$ ${\displaystyle P_{S}}$ ${\displaystyle n}$ ${\displaystyle n}$

District loyalty

Be a hyperplane in . If and , it follows from the plane equation of and the Cauchy-Schwarz inequality : ${\displaystyle E:\sum _{i=1}^{n+1}a_{i}\cdot x_{i}=b}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle x=(x_{1},\ldots ,x_{n+1})^{t}\in \mathbb {S} ^{n}\cap E}$ ${\displaystyle a=(a_{1},\ldots ,a_{n+1})}$ ${\displaystyle E}$

${\displaystyle 1=\|{\frac {a}{\|a\|}}\|\cdot \|x\|\geq {\frac {a}{\|a\|}}\cdot x\Rightarrow a\cdot x\leq \|a\|\Leftrightarrow {\sqrt {\sum _{i=1}^{n+1}a_{i}^{2}}}\geq \sum _{i=1}^{n+1}a_{i}x_{i}=b\Rightarrow {\frac {a_{n+1}+b}{a_{n+1}-b}}+\sum _{i=1}^{n}{\frac {a_{i}^{2}}{(a_{n+1}-b)^{2}}}\geq 0}$

The image of the points of the plane through satisfies the equation: ${\displaystyle P_{N}}$

${\displaystyle a_{1}{\frac {2y_{1}}{\|y\|^{2}+1}}+\cdots +a_{n}{\frac {2y_{n}}{\|y\|^{2}+1}}+a_{n+1}{\frac {\|y\|^{2}-1}{\|y\|^{2}+1}}=b\Leftrightarrow \sum _{i=1}^{n}\left(y_{i}-{\frac {-a_{i}}{a_{n+1}-b}}\right)^{2}={\frac {a_{n+1}+b}{a_{n+1}-b}}+\sum _{i=1}^{n}{\frac {a_{i}^{2}}{(a_{n+1}-b)^{2}}}}$

This is an equation of spheres . Therefore maps all sections from and to any hyperplane, especially spheres that lie in this hyperplane, onto spheres in . ${\displaystyle P_{N}}$ ${\displaystyle \mathbb {S} ^{n}}$ ${\displaystyle \mathbb {R} ^{n}}$

Compactification of the complex number level

→ Main article : Riemann number ball

The stereographic projection can, among other things, be used to compact the complex number plane . One adds an additional point, which is referred to here with . The set is called the one-point compactification of or Riemann number sphere . ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {C} \cong \mathbb {R} ^{2}}$ ${\displaystyle \infty }$ ${\displaystyle {\hat {\mathbb {C} }}}$ ${\displaystyle \mathbb {C} }$

The figure is created by means of the figure ${\displaystyle P_{N}}$

${\displaystyle {\begin{aligned}{\hat {P_{N}}}\colon \mathbb {S} ^{2}&\to {\hat {\mathbb {C} }}=\mathbb {C} \cup \{\infty \}\\(x_{1},x_{2},x_{3})&\mapsto {\begin{cases}P_{N}(x_{1},x_{2},x_{3}),&\mathrm {f{\ddot {u}}r} \ (x_{1},x_{2},x_{3})\neq (0,0,1)\\\infty ,&\mathrm {f{\ddot {u}}r} \ (x_{1},x_{2},x_{3})=(0,0,1)\end{cases}}\end{aligned}}}$

continued. One calls now open exactly when open is in. This induces a topology. ${\displaystyle U\subset {\hat {\mathbb {C} }}=\mathbb {C} \cup \{\infty \}}$ ${\displaystyle \sigma ^{-1}(U)}$ ${\displaystyle \mathbb {S} ^{2}}$ ${\displaystyle {\hat {\mathbb {C} }}}$

Chordal metric

→ Main article : Chordal metric

The same topology is achieved by the

${\displaystyle \chi (z,w):=\|P_{N}^{-1}(z)-P_{N}^{-1}(w)\|_{2}}$

induced defined chordal metric . ${\displaystyle \chi }$

See also

• Planisphere
• Universal polar stereographic projection
• Wulff's network
• Möbius level

literature

Sources for the mathematical explanations:

• Konrad Königsberger : Analysis. Volume 2. Springer-Verlag, Berlin a. a. 1993, ISBN 3-540-54723-1 .

General description n-dim. Sphere: Section 1.3.II, Conformity: Section 3.1.

• Günter Scheja, Uwe Storch : Textbook of Algebra. Volume 1. 2nd revised and expanded edition. Teubner, Stuttgart 1994, ISBN 3-519-12203-0 .

Projective representation: Section VH Ex. 4.

• Günther Bollman, Günther Koch (ed.): Lexicon of cartography and geomatics. Volume 1: A to Karti. Spectrum Academic Publishing House, Heidelberg u. a. 2001, ISBN 3-8274-1055-X .

Web links

Commons : Stereographic Projection  - collection of images, videos and audio files

• Animated explanation of the stereographic projection (German)
• Interactive three-dimensional representation of the stereographic projection (English; Java applet )
• Comparison of different projections .

Individual evidence

1. ↑ ^{a b} Mathematik.de: Circular related figures.
2. ^ Guido Schmitz: Materialphysik I. Lecture notes. University of Münster, 2012, p. 2 f.
3. ^ Jean-Pierre Burg: Structural geology: structural analysis of the polyphase defromation. Lecture notes (Chapter 10), ETH Zurich, 2017, p. 287 ff.
4. ^ Elena Perk: Stereographic projection. ( Memento of the original from January 11, 2016 in the Internet Archive ) Info: The archive link was inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice. P. 2. 
5. ↑ Karl Horst Meyer: stereographic projection. P. 12.
6. ↑ A fundamental difference is the mirror image of the sky on the astrolabe, because ancient astronomers preferred the view of the celestial sphere from outside.
7. ↑ Here you can divide through . Because if this were equal to 0, the North Pole would be in the plane. ${\displaystyle a_{n+1}-b}$