Central projection

Central projection of a cube

Parallel projection or central projection of a row of houses

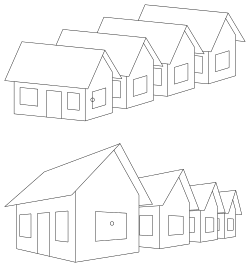
With the help of the central projection, vivid images of spatial objects can be produced in the representing geometry . In contrast to parallel projection, in which parallel rays are used to project onto a plane (image table), central projection uses rays (straight lines) through a fixed point , the eye point. The central projection creates images like those created when looking with one eye in the eye point. While parallel straight lines are mapped onto the same in parallel projection, parallel straight lines that do not run parallel to the image table are mapped onto straight lines that intersect at a point, the vanishing point , in central projection . Central projections reflect the spatial impression of an object much better than a parallel projection (see row of houses). The central projection corresponds to the image of the environment by the human eye and thus results in a natural image impression. It is used in technology and architecture , in cartography , in painting and drawing , as well as in computer graphics . ${\displaystyle O}$

Designations

Central projection: designations

Vanishing and tracking points of straight lines

House with two vanishing points or one vanishing point

Example with a circle of vision

Variation of image plate and eye point

How a pinhole camera works

The eye point , the center of the projection rays of a central projection, is usually designated with O, which creates a relationship to the eye (Latin: oculus = eye). The plumb point from the eye point on the image board is called the main point , as it plays an important role in the creation of a central projection and in the subsequent viewing. The main point is, so to speak, the center of the picture. The distance between the eye point and the image table is called the distance (the current central projection). If the main point is marked in the picture and the distance is known, you know where to position your eye when looking at the picture in order to get a perfect impression. The vanishing point of a parallel bundle of lines that is not parallel to the image table is the common point of intersection of the associated image line and is always the point of intersection with the image table (trace point) of that line of the bundle that contains the eye point (see image). Straight lines that are parallel to the picture table have no vanishing points or one says that the associated vanishing point is at "infinity". A straight line that runs perpendicular to the table is called a depth line . The vanishing point of all contour lines is the main point. With many objects, horizontal lines and thus their vanishing points play an important role. The vanishing points of all horizontal directions together form the horizon h , a horizontal straight line. If the picture board is vertical, the main point is always on the horizon. Cuboid objects have a) three natural vanishing points if none of the edges is parallel to the picture board (see picture of the cube in the first picture), b) two vanishing points if one edge is parallel to the picture board (see 1st house), c) a vanishing point if two directions run parallel to the drawing (see 2nd house). The last case is called a frontal perspective . Mostly, central projections of objects are made with the help of elevations and floor plans. The floor plan level is referred to as the level (of the viewer) based on photography . The line of intersection (track line) s of the floor plan (standing plane) with the picture board is often drawn into the picture for technical reasons and is called the standing line . The base line and the horizon are always parallel to each other. With the help of rays through the eye point O, all points in space except the points in the plane parallel to the image table can be mapped through the eye point. The points of this plane are called vanishing points and the plane is called vanishing plane . When looking at a central projection, one often has the impression that peripheral areas appear distorted. This is always due to the fact that you have not positioned your eye in the eye point. Experience has shown that the area of ​​the image, which can still be seen when the eye is positioned at the eye point and the main point is fixed, is conically restricted. The intersection of this cone of vision with the illustration is the circle of vision (see image of a bridge). Its radius is approximately 0.58 * distance. This corresponds to half an opening angle of the cone of vision of 30 °. ${\displaystyle \pi _{v}}$ ${\displaystyle \pi _{v}}$

In the representational geometry, objects are always shown “in front of” the vanishing plane, i. H. The object and the illustration are on the same side of the vanishing plane. In photography , the object and the image are always on different sides of . As a result, photographic images in the camera are always "upside down", which has no effect on how they are viewed later, as the image is then simply held "the right way round". ${\displaystyle \pi _{v}}$ ${\displaystyle \pi _{v}}$

The advantage of a central projection is that it provides very clear images, namely images that imitate seeing (with one eye) or taking photos. However, lengths from a central projection or even only ratios of lengths cannot be read off. In contrast to the parallel projection, which is true to the relationship , with a central projection only the double ratio (ratio of ratios) remains invariant.

The central projection shows objects in the edge area too large. Thus, the fields of a chess board, which is parallel to the picture board, are all shown the same size and square. In fact, the fields that are further away from the main point are also further away from the viewer and would have to be shown smaller on the picture board in order to obtain a natural image. Indeed, this effect is visible when imaging with fisheye lenses . However, the human eye corrects the resulting crooked edges when looking at large, close objects, so that the fisheye perspective does not appear natural.

Many wide-angle lenses therefore approximate the central perspective by displaying image areas close to the edge in an enlarged manner so that the straight lines lying parallel to the image table are also shown as straight as possible. Although this leads to certain distortions in the corners of the image, these are not perceived as annoying in architectural photography and cause a certain, possibly desirable drama in landscape photography, while the depiction of groups of people with a wide-angle lens often leads to unsatisfactory results. Video recordings with wide angle lead to unnatural "flowing" of the objects in the edge areas when panning. The relationships described are more noticeable for focal lengths with cones of vision than for human.

On the meaning of the main point, distance and eye point

The picture with variations of a house shows the importance of the main parameters main point, distance and eye point. If one holds the eye point and pushes the picture panel towards the eye point, i. H. if the distance is shortened, the image is merely reduced to an image similar to the first image. The angles are retained. If, on the other hand, one holds the picture plate and pushes the eye point towards the main point, i. H. Here, too, the distance is shortened, creating a picture with a new visual effect. The picture is no longer similar to the first picture. Corresponding angles are no longer the same. Shifting the main point along the straight line only causes the image to be reduced or enlarged. A shift along the eye point causes a significant change in the image. ${\displaystyle O}$ ${\displaystyle O}$ ${\displaystyle OH}$ ${\displaystyle OH}$

Construction of the central projection of an object

The construction of a central projection of an object is significantly more complex than a parallel projection. There is a process for this that is similar to the incision process for parallel projections: the architect arrangement . As with the incision process, the floor plan and elevation must be specially positioned. For the construction of the picture only points are connected and lines are cut. Parallels play an important facilitating role in parallel projection. They are also of great help with central projection thanks to their vanishing points. Another relatively simple method is the frontal perspective . It is similar to the cavalier's perspective for a parallel projection (see axonometry ). In the frontal perspective, the panel is to an essential plane of the object, e.g. B. a house front, parallel or the picture panel and this essential level are identical. The latter has the great advantage that you can simply expand the elevation of the object into a frontal perspective. Another important advantage of a frontal perspective is that circles in the essential level are mapped back to circles (see example in frontal perspective). However, there is also a disadvantage: the front plane of the object is strongly emphasized. This is mostly not the case with a central projection with two essential vanishing points.

Projection formulas

To the projection formulas: Basis of the picture table

For an analytical description of the central projection, we choose in the image table

• the main point as the coordinate origin of a new coordinate system and ${\displaystyle H:{\mathbf {h} }}$
• the normal unit vector of the image table pointing from to the eye point . ${\displaystyle \mathbf {n} _{0}}$ ${\displaystyle H}$ ${\displaystyle O}$

With the distance applies: . ${\displaystyle d}$ ${\displaystyle O:{\mathbf {h} }+d{\mathbf {n} }_{0}}$

• We add unit vectors in such a way that ${\displaystyle {\mathbf {n} }_{0}}$ ${\displaystyle {\mathbf {e} }_{1},{\mathbf {e} }_{2}}$

a) is horizontal and b) form an orthonormal system (see picture). ${\displaystyle {\mathbf {e} }_{1}}$ ${\displaystyle \{{\mathbf {e} }_{1},{\mathbf {e} }_{2},{\mathbf {n} }_{0}\}}$

The central projection of an object point is carried out in two steps: ${\displaystyle P}$

1. Coordinate transformation of the point into the system with the zero point and the base : ${\displaystyle P:{\mathbf {p} }=(x,y,z)}$ ${\displaystyle (H;{\mathbf {e} }_{1},{\mathbf {e} }_{2},{\mathbf {n} }_{0})}$ ${\displaystyle H}$ ${\displaystyle \{{\mathbf {e} }_{1},{\mathbf {e} }_{2},{\mathbf {n} }_{0}\}}$

   ${\displaystyle {\mathbf {p} }=(x,y,z)\to {\bar {\mathbf {p} }}=({\bar {x}},{\bar {y}},{\bar {z}})}$ With

   ${\displaystyle {\bar {x}}=({\mathbf {p} }-{\mathbf {h} })\cdot {\mathbf {e} }_{1},\quad {\bar {y}}=({\mathbf {p} }-{\mathbf {h} })\cdot {\mathbf {e} }_{2},\quad {\bar {z}}=({\mathbf {p} }-{\mathbf {h} })\cdot {\mathbf {n} }_{0},}$

2. Central projection in the system on the - plane: ${\displaystyle (H;{\mathbf {e} }_{1},{\mathbf {e} }_{2},{\mathbf {n} }_{0})}$ ${\displaystyle {\bar {x}}-{\bar {y}}}$

   ${\displaystyle {\bar {\mathbf {p} }}=({\bar {x}},{\bar {y}},{\bar {z}})\to \left({\frac {\bar {x}}{1-{\bar {z}}/d}},{\frac {\bar {y}}{1-{\bar {z}}/d}}\right)}$

A clear description of the normal vector can be obtained by using the angular coordinates of the spherical coordinates . The angle describes (in radians) the longitude and latitude: ${\displaystyle {\mathbf {n} }_{0}}$ ${\displaystyle u,v}$ ${\displaystyle u}$ ${\displaystyle v}$

${\displaystyle {\mathbf {n} }_{0}=(\cos u\cos v,\sin u\cos v,\sin v),\quad u\in [0,2\pi ],v\in \left[{\frac {-\pi }{2}},{\frac {\pi }{2}}\right]}$

For the vectors we then get: ${\displaystyle {\mathbf {e} }_{1},{\mathbf {e} }_{2}}$

${\displaystyle {\mathbf {e} }_{1}=(-\sin u,\cos u,0),\quad {\mathbf {e} }_{2}:=(-\cos u\sin v,-\sin u\sin v,\cos v)}$.

In order to establish a specific central projection,

a) the main point , b) the distance and c) the two angles are given. ${\displaystyle H}$ ${\displaystyle d}$ ${\displaystyle u,v}$

So a total of 6 numbers are required.

Note: The formulas for vertical parallel projection are obtained for. Since the main point no longer plays a role here, you can bet. It can be seen that a perpendicular parallel projection is described by a linear mapping . This does not apply to a central projection. However: Using homogeneous coordinates , as is usual in computer vision, one can also display a central projection as a linear image (see projection matrix_ (computer vision) ). ${\displaystyle d\to \infty }$ ${\displaystyle H:(0,0,0)}$

Note: When evaluating measurement images in photogrammetry, other parameters are used, see chap. Orientation .

Applications of central projection

clearly recognizable alignment lines of the central projection

Typical applications of the central projection can be found:

• in descriptive geometry
• in architecture in the perspective graphic representation of objects,
• in painting and drawing
• in computer graphics
• in photography e.g. B. in the reconstruction of buildings from photographs
• in photogrammetry e.g. B. when evaluating and measuring (aerial) images, correcting oblique recordings ,
• in cartography ( called azimuthal projection there), for map network designs ( gnomonic projection ; stereographic projection ),
• in the gnomonic of the theory of the sundial to depict the sun on a dial.

literature

• Fucke, Kirch, Nickel: Descriptive Geometry. Fachbuch-Verlag, Leipzig 1998, ISBN 3-446-00778-4 .
• Cornelie Leopold: Geometric Basics of Architectural Representation. Verlag W. Kohlhammer, Stuttgart 2005, ISBN 3-17-018489-X .
• Fritz Reinhardt, Heinrich Soeder: dtv atlas for mathematics, blackboard and texts, volume I, fundamentals, algebra and geometry. Deutscher Taschenbuch Verlag, Munich 1982.
• W. Rüger, J. Pietschner, K. Regensburger: Photogrammetry, procedures and devices. VEB Verlag für Bauwesen, Berlin 1978.

Web links

• Descriptive geometry for architects (PDF; 1.5 MB). Script (Uni Darmstadt)
• CDKG: Computer-aided Descriptive and Constructive Geometry (TU Darmstadt) (PDF; 3.4 MB), pp. 37–39

Commons : Central projection  - collection of images, videos and audio files