
Axis reflection as an example of a linear mapping
A linear mapping (also called linear transformation or vector space homomorphism ) is an important type of mapping between two vector spaces over the same field in linear algebra . In the case of a linear mapping, it is irrelevant whether you add two vectors first and then map their sum, or map the vectors first and then add the sum of the images. The same applies to the multiplication with a scalar from the basic body.
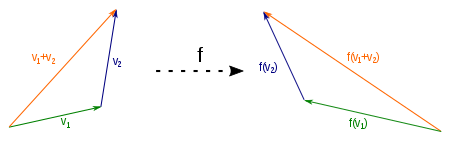
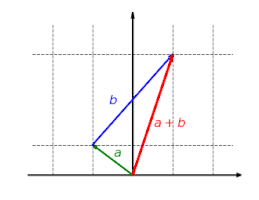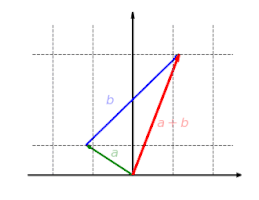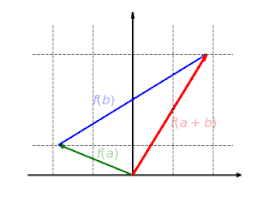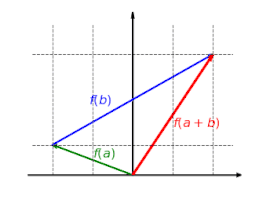
The example shown of a reflection on the Y-axis illustrates this. The vector is the sum of the vectors and and its image is the vector . But you also get if you add the images and the vectors and .









One then says that a linear mapping is compatible with the combinations of vector addition and scalar multiplication . The linear mapping is thus a homomorphism (structure-preserving mapping) between vector spaces.
In functional analysis , when considering infinitely dimensional vector spaces that carry a topology , one usually speaks of linear operators instead of linear mappings. From a formal point of view, the terms are synonymous. In the case of infinite-dimensional vector spaces, however, the question of continuity is significant, while continuity is always present for linear mappings between finite-dimensional real vector spaces (each with the Euclidean norm ) or, more generally, between finite-dimensional Hausdorff topological vector spaces .
definition
Be and vector spaces over a common basic body . A mapping is called a linear mapping if all and the following conditions apply:






-
 is homogeneous:
is homogeneous:

-
 is additive:
is additive:

The two conditions above can also be summarized:

For this goes into the condition for the homogeneity and for the one for the additivity. Another, equivalent condition is the requirement that the graph of the mapping is a subspace of the sum of the vector spaces and .





Explanation
A mapping is linear if it is compatible with the vector space structure. In other words: linear mappings are compatible with both the underlying addition and scalar multiplication of the domain of definition and value. The compatibility with the addition means that the linear mapping receives sums. If we have a sum with in the definition area, then this sum is valid and thus remains in the value area according to the illustration:





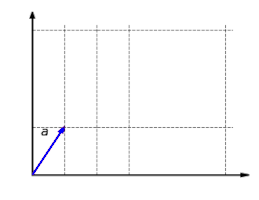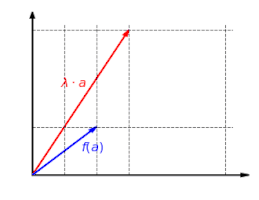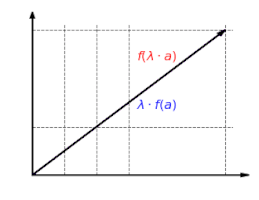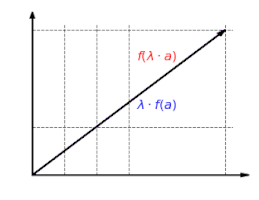
This implication can be shortened by putting the premise in . This is how you get the demand . The compatibility with scalar multiplication can be described analogously. This is fulfilled if it follows from the connection with the scalar and in the definition range that the following also applies in the value range:








After inserting the premise into the conclusion , one receives the demand .



Visualization of the compatibility with scalar multiplication: Each scaling is retained by a linear mapping and it applies .


Examples
- For every linear mapping has the shape with .



- It be and . Then a linear mapping is defined for each matrix with the help of matrix multiplication . Any linear mapping from to can be represented in this way.








- Is an open interval of the vector space of the continuously differentiable functions and the vector space of the continuous functions on , so the picture is , , the each function assigns its derivative, linear. The same applies to other linear differential operators .










This figure is additive: It does not matter if only adding vectors and then mapping or whether only maps the vectors and then added: .

This figure is homogeneous: it does not matter if you only scaled a vector and then mapping or whether only maps and then scales the vector: .

Image and core
Two sets of importance when looking at linear maps are the image and the core of a linear map .

- The image of the illustration is the set of image vectors below , i.e. the set of all with out . The amount of images is therefore also noted by. The image is a subspace of .







- The core of the mapping is the set of vectors from which are mapped onto the zero vector of by. It is a subspace of . The mapping is injective if and only if the kernel contains only the zero vector.






properties
- A linear map between vector spaces and forms the zero vector of the zero vector from from: because






- The homomorphism theorem describes a relationship between the core and the image of a linear mapping : The factor space is isomorphic to the image .



Linear mappings between finite-dimensional vector spaces
Base

Summary of the properties of injective and surjective linear mappings
A linear mapping between finite-dimensional vector spaces is uniquely determined by the images of the vectors of a basis . If the vectors form a basis of the vector space and are vectors in , then there is exactly one linear mapping that maps onto , onto , ..., onto . If any vector is off , it can be clearly represented as a linear combination of the basis vectors:














Here are the coordinates of the vector with respect to the base . His image is given by





The mapping is injective if and only if the image vectors of the basis are linearly independent . It is surjective if and only if it spans the target area .




If one assigns to each element of a base of a vector from arbitrarily, so it is possible with the above formula to a linear mapping, this assignment clearly continue.





If the image vectors are represented with respect to a base of , this leads to the matrix representation of the linear mapping.


Mapping matrix
Are and finite, , , and are bases of and from where, each linear mapping may by a - matrix are presented. This is obtained as follows: For each basis vector from , the image vector can be represented as a linear combination of the basis vectors :
















The , , are the entries of the matrix :





The -th column contains the coordinates of with respect to the base .



With the help of this matrix one can calculate the image vector of each vector
:



For the coordinates of respect so true



-
 .
.
This can be expressed using matrix multiplication:

The matrix is called the mapping matrix or representation matrix of . Other spellings for are and .




![_ {B '} [f] _B](https://wikimedia.org/api/rest_v1/media/math/render/svg/062cd3a0f31d7327c7da18cc418a016a9c4a0279)
Dimensional formula
Image and core are related via the set of dimensions. This states that the dimension is equal to the sum of the dimensions of the image and the core:


Linear mappings between infinite-dimensional vector spaces
In functional analysis in particular , one considers linear mappings between infinite-dimensional vector spaces. In this context, the linear mappings are usually called linear operators. The vector spaces considered mostly still have the additional structure of a normalized complete vector space. Such vector spaces are called Banach spaces . In contrast to the finite-dimensional case, it is not sufficient to investigate linear operators only on a basis. According to Baier's category theorem , a basis of an infinite-dimensional Banach space has an uncountable number of elements and the existence of such a basis cannot be justified constructively, i.e. only using the axiom of choice . A different basic term is therefore used, such as orthonormal bases or more generally shudder bases . This means that certain operators such as Hilbert-Schmidt operators can be represented using "infinitely large matrices", whereby infinite linear combinations must then also be permitted.
Special linear maps
- Monomorphism
- A monomorphism between vector spaces is a linear mapping that is injective . This applies precisely when the column vectors of the representation matrix are linearly independent.

- Epimorphism
- An epimorphism between vector spaces is a linear mapping that is surjective . This is the case if and only if the rank of the representation matrix is equal to the dimension of .


- Isomorphism
- An isomorphism between vector spaces is a linear mapping that is bijective . This is exactly the case when the display matrix is regular . The two spaces and are then called isomorphic.



- Endomorphism
- A endomorphism between vector spaces is a linear map, in which the spaces and are equal to: . The representation matrix of this figure is a square matrix.



- Automorphism
- An automorphism between vector spaces is a bijective linear mapping in which the spaces and are equal. So it is both an isomorphism and an endomorphism. The display matrix of this figure is a regular matrix.


Linear figures vector space

Formation of the vector space L (V, W)
The set of linear mappings from a -vector space into a -vector space is a vector space over , more precisely: a subspace of the -vector space of all mappings from to . This means that the sum of two linear mappings and , component-wise defined by












again is a linear mapping and that the product

a linear mapping with a scalar is also a linear mapping again.

If the dimension and the dimension , and are given in a base and a base , then is the mapping









an isomorphism in the matrix space . The vector space thus has the dimension .



If you consider the set of linear self-mappings of a vector space, i.e. the special case , then these not only form a vector space, but also an associative algebra with the concatenation of mappings as multiplication , which is briefly referred to as


generalization
A linear mapping is a special case of an affine mapping .
If the body is replaced by a ring in the definition of the linear mapping between vector spaces , a module homomorphism is obtained .
Notes and individual references
-
↑ This set of linear mappings is sometimes also written as.

literature
-
Albrecht Beutelspacher : Linear Algebra. An introduction to the science of vectors, maps, and matrices. 6th, revised and supplemented edition. Vieweg Braunschweig et al. 2003, ISBN 3-528-56508-X , pp. 124-143.
- Günter Gramlich: Linear Algebra. An introduction for engineers. Fachbuchverlag Leipzig in Carl-Hanser-Verlag, Munich 2003, ISBN 3-446-22122-0 .
- Detlef Wille: Repetition of Linear Algebra. Volume 1. 4th edition, reprint. Binomi, Springe 2003, ISBN 3-923923-40-6 .
Web links















































































































![_ {B '} [f] _B](https://wikimedia.org/api/rest_v1/media/math/render/svg/062cd3a0f31d7327c7da18cc418a016a9c4a0279)















