Factor space

The quotient vector space , also called quotient space or factor space for short , is a term from linear algebra , a branch of mathematics . It is the vector space that arises as an image of a parallel projection along a sub-vector space . The elements of the quotient vector space are equivalence classes.

definition

Let it be a vector space over a field and a subspace of . By fixing ${\ displaystyle V}$ ${\ displaystyle K}$ ${\ displaystyle U}$ ${\ displaystyle V}$

{\ displaystyle v_ {1} \ sim v_ {2} \;: \! \ iff v_ {1} -v_ {2} \ in U}

For

{\ displaystyle v_ {1}, v_ {2} \ in V}

is defined on an equivalence relation . ${\ displaystyle V}$

The vectors and are therefore equivalent if they differ by one vector . In other words: If the line through the points and to parallel are is, and equivalent. ${\ displaystyle v_ {1}}$ ${\ displaystyle v_ {2}}$ ${\ displaystyle U}$ ${\ displaystyle v_ {1}}$ ${\ displaystyle v_ {2}}$ ${\ displaystyle U}$ ${\ displaystyle v_ {1}}$ ${\ displaystyle v_ {2}}$

The equivalence class of a point is ${\ displaystyle v}$

{\ displaystyle [v]: = v + U: = \ {v + u \ mid u \ in U \}}

,

clearly shows the "parallel" affine subspace . The equivalence classes are also known as secondary classes (this term comes from group theory ). ${\ displaystyle U}$ ${\ displaystyle v}$

The quotient vector space from to is the set of all equivalence classes and is denoted by: ${\ displaystyle V}$ ${\ displaystyle U}$ ${\ displaystyle V / U}$

{\ displaystyle V / U: = \ {[v] \ mid v \ in V \}}

.

It forms a vector space if the vector space operations are defined by proxy:

${\ displaystyle [v_ {1}] + [v_ {2}] = [v_ {1} + v_ {2}]}$
${\ displaystyle \ lambda \ cdot [v] = [\ lambda v]}$

for and . ${\ displaystyle v, v_ {1}, v_ {2} \ in V}$ ${\ displaystyle \ lambda \ in K}$

These operations are well-defined, i.e. independent of the choice of representatives.

properties

There is a canonical surjective linear mapping

{\ displaystyle \ pi \ colon \; V \ to V / U, \; v \ mapsto [v]}

.

Is a complement of in , i.e. H. is the direct sum of and , the restriction of to is an isomorphism . But there is no canonical possibility to understand it as a subspace of . ${\ displaystyle W}$ ${\ displaystyle U}$ ${\ displaystyle V}$ ${\ displaystyle V}$ ${\ displaystyle U}$ ${\ displaystyle W}$ ${\ displaystyle \ pi}$ ${\ displaystyle W}$ ${\ displaystyle V / U}$ ${\ displaystyle V}$

If it is finite-dimensional, then the following relationship results for the dimensions: ${\ displaystyle V}$

{\ displaystyle \ dim U + \ dim V / U = \ dim V}

The dual space of can be identified with those linear forms on that are identical on. ${\ displaystyle V / U}$ ${\ displaystyle V}$ ${\ displaystyle U}$ ${\ displaystyle 0}$

The homomorphism theorem states that a linear mapping has an isomorphism ${\ displaystyle f \ colon \; V \ to W}$

{\ displaystyle V / (\ ker f) \ to \ mathrm {im} \, f}

between the quotient space from after the kernel from and the image from induced, d. H. the concatenation

{\ displaystyle V}

{\ displaystyle f}

{\ displaystyle f}

{\ displaystyle V \ longrightarrow V / (\ ker f) \ longrightarrow \ mathrm {im} \, f \ longrightarrow W}

is the same .

{\ displaystyle f}

Application in functional analysis

Many normed spaces created in the following way: Be a real or complex vector space and let 1 seminorm on . Then is a subspace of . The quotient space then becomes a normalized vector space with the norm . ${\ displaystyle V}$ ${\ displaystyle p}$ ${\ displaystyle V}$ ${\ displaystyle U = \ {v \ in V \ mid p (v) = 0 \}}$ ${\ displaystyle V}$ ${\ displaystyle V / U}$ ${\ displaystyle [v] \ mapsto p (v)}$

More general: Let be a topological vector space that is not Hausdorffian . Then be analogous to above subspace define: . The quotient space with the quotient topology becomes a Hausdorff topological vector space. ${\ displaystyle V}$ ${\ displaystyle U = \ {v \ in V \ mid {\ text {Each}} 0 {\ text {-Environment contains}} v \} = {\ overline {\ {0 \}}}}$ ${\ displaystyle V / U}$

Examples

abstract

The spaces and thus also the Sobolew spaces are quotient vector spaces. ${\ displaystyle L ^ {p}}$

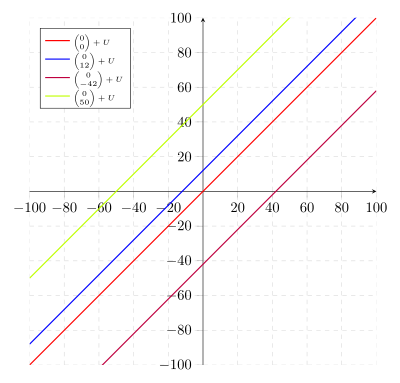
Concrete

The vector space and the one-dimensional sub-vector space are given . Then for example ${\ displaystyle V = \ mathbb {R} ^ {2}}$ ${\ displaystyle U = \ left \ {\ left. {\ bigl (} {\ begin {smallmatrix} x \\ x \ end {smallmatrix}} {\ bigr)} \ right | x \ in \ mathbb {R} \ right \}}$