An orthonormal basis (ONB) or a complete orthonormal (VONS) is in the mathematical areas linear algebra and functional analysis a set of vectors of a vector space with scalar product ( inner product space ) formed on the length of one normalized , mutually orthogonal (hence ortho-normal basis ) and their linear hull is dense in vector space. In the finite-dimensional case this is a basis of the vector space. In the infinite-dimensional case it is not a matter of a vector space basis in the sense of linear algebra.
If one waives the condition that the vectors are normalized to the length one, one speaks of an orthogonal basis .
The concept of the orthonormal basis is of great importance both in the case of finite dimensions and for infinitely dimensional spaces, in particular Hilbert spaces .
Finite-dimensional spaces
In the following we assume a finite-dimensional inner product space, that is, a vector space over or with a scalar product . In the complex case it is assumed that the scalar product is linear in the second argument and semilinear in the first, i.e.





for all vectors and all . The norm induced by the scalar product is denoted by.



Definition and existence
An orthonormal basis of a -dimensional interior product space is understood to be a basis of , which is an orthonormal system , that is:




- Every basis vector has the norm one:
-
 for everyone .
for everyone .
- The basis vectors are orthogonal in pairs:
-
 for everyone with .
for everyone with .

Every finite-dimensional vector space with a scalar product has an orthonormal basis. With the help of the Gram-Schmidt orthonormalization method, every orthonormal system can be supplemented to an orthonormal basis.
Since orthonormal systems are always linearly independent , an orthonormal system of vectors already forms an orthonormal basis in a -dimensional interior product space.


Handedness of the base
Let an ordered orthonormal basis of . Then is the matrix


formed from the vectors noted as column vectors orthogonally and therefore has the determinant +1 or −1. If so , the vectors form a legal system .



Examples
- example 1
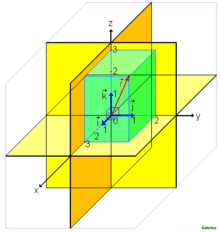
- The standard basis of the , consisting of the vectors


- is an orthonormal basis of the three-dimensional Euclidean vector space (equipped with the standard scalar product ): It is a basis of , each of these vectors has the length 1, and two of these vectors are perpendicular to one another, because their scalar product is 0.


- More generally, in coordinate space or , provided with the standard scalar product, the standard basis is an orthonormal basis.



- Example 2
- The two vectors
-
![\ vec b_1 = \ begin {pmatrix} \ tfrac 3 5 \\ [1ex] \ tfrac 4 5 \ end {pmatrix}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f2f7a2640fbbcce46837d1ee2c3254eca1f4840) and
and ![\ vec b_2 = \ begin {pmatrix} - \ tfrac {4} 5 \\ [1ex] \ tfrac 3 5 \ end {pmatrix}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6680591589975dbdb6095da762f53f080026c289)
- together with the standard scalar product form an orthonormal system and therefore also an orthonormal basis of .


Coordinate representation with respect to an orthonormal basis
Vectors
If is an orthonormal basis of , then the components of a vector can be calculated particularly easily as orthogonal projections with respect to this basis . Has the representation
regarding the base





so applies
-
 For
For 
because

and thus

In example 2 above, the following applies to the vector :

-
 and
and

and thus
![\ vec v = \ frac {34} 5 \, \ vec b_1 + \ frac {13} 5 \, \ vec b_2 = \ frac {34} 5 \, \ begin {pmatrix} \ tfrac 3 5 \\ [1ex] \ tfrac 4 5 \ end {pmatrix} + \ frac {13} 5 \, \ begin {pmatrix} - \ tfrac {4} 5 \\ [1ex] \ tfrac 3 5 \ end {pmatrix}.](https://wikimedia.org/api/rest_v1/media/math/render/svg/511537ffc555c451aef3b6f0c1dd6cc7e0cb8f15)
The scalar product
In coordinates with respect to an orthonormal basis, each scalar product has the form of the standard scalar product. More accurate:
Is an orthonormal basis of and have the vectors and with respect to the coordinate representation
and , then applies








in the real case, resp.

in the complex case.
Orthogonal mappings
Is an orthogonal (in the real case) or a unitary transformation (in the complex case) and is an orthonormal basis of , as is the representation matrix of relative to the base an orthogonal or a unitary matrix .





This statement is incorrect with regard to any base.
Infinite dimensional spaces
definition
Let be a Prehilbert space and let be the norm induced by the scalar product. A subset is called an orthonormal system if and for all with .







An orthonormal system, the linear envelope of which lies close in space, is called an orthonormal basis or Hilbert basis of space.
It should be noted that in the sense of this section, in contrast to the finite dimension, an orthonormal basis is not a Hamel basis , i.e. not a basis in the sense of linear algebra. This means that an element from cannot generally be represented as a linear combination of finitely many elements from , but only with a countable infinite number, i.e. as an unconditionally convergent series .


characterization
The following statements are equivalent for a Prehilbert dream:

-
 is an orthonormal basis.
is an orthonormal basis.
-
 is an orthonormal system and Parseval's equation applies :
is an orthonormal system and Parseval's equation applies :
-
 for everyone .
for everyone .
If it is even complete, i.e. a Hilbert space , this is also equivalent to:

- The orthogonal complement of is the null space, because in general for a subset that .




- More concretely: It applies if and only if the scalar product is for all .



-
 is a maximal orthonormal system with regard to inclusion, i. H. every orthonormal system that contains is the same . If a maximal were not an orthonormal system, then a vector would exist in the orthogonal complement; if this were normalized and added to , an orthonormal system would again be obtained.
is a maximal orthonormal system with regard to inclusion, i. H. every orthonormal system that contains is the same . If a maximal were not an orthonormal system, then a vector would exist in the orthogonal complement; if this were normalized and added to , an orthonormal system would again be obtained.



existence
With Zorn's lemma it can be shown that every Hilbert space has an orthonormal basis: Consider the set of all orthonormal systems with the inclusion as a partial order. This is not empty because the empty set is an orthonormal system. Every ascending chain of such orthonormal systems with regard to inclusion is limited upwards by the union: If the union were not an orthonormal system, it would contain one non-normalized or two different non-orthogonal vectors, which should already have occurred in one of the combined orthogonal systems. According to Zorn's lemma, there is thus a maximal orthonormal system - an orthonormal basis. Instead of all orthonormal systems, one can only consider the orthonormal systems that contain a given orthonormal system. Then one obtains analogously that every orthonormal system can be supplemented to an orthogonal basis.


Alternatively, the Gram-Schmidt method can be applied to or any dense subset and one obtains an orthonormal basis.

Every separable Prähilbert space has an orthonormal basis. To do this, choose a (at most) countable dense subset and apply the Gram-Schmidt method to this. Completeness is not necessary here, since projections only need to be carried out onto finite-dimensional subspaces, which are always complete. This gives a (at most) countable orthonormal basis. Conversely, every Prehilbert space is also separable with a (at most) countable orthonormal basis.
Development according to an orthonormal basis
A Hilbert space with an orthonormal basis has the property that for each the series representation



applies. This series necessarily converges . If the Hilbert space is finite-dimensional, the concept of unconditional convergence coincides with that of absolute convergence . This series is also called a generalized Fourier series . If one chooses the Hilbert space of real-valued square-integrable functions with the scalar product
![L ^ 2 ([0.2 \ pi])](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f3f1c02125a3b161aad32d469cda6a21baff682)

then

With
-
 for and
for and![x \ in [0.2 \ pi]](https://wikimedia.org/api/rest_v1/media/math/render/svg/8cedb963595290bb4f2f9e0b1e140ba8432ccd8b)

an orthonormal system and even an orthonormal basis of . Regarding this base are
![L ^ 2 ([0.2 \ pi])](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f3f1c02125a3b161aad32d469cda6a21baff682)


and

just the Fourier coefficients of the Fourier series of . Hence the Fourier series is the series representation of an element from with respect to the given orthonormal basis.

![L ^ 2 ([0.2 \ pi])](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f3f1c02125a3b161aad32d469cda6a21baff682)
Further examples
Let be the sequence space of the square summable sequences. The set is an orthonormal basis of .



literature



























![\ vec b_1 = \ begin {pmatrix} \ tfrac 3 5 \\ [1ex] \ tfrac 4 5 \ end {pmatrix}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f2f7a2640fbbcce46837d1ee2c3254eca1f4840)
![\ vec b_2 = \ begin {pmatrix} - \ tfrac {4} 5 \\ [1ex] \ tfrac 3 5 \ end {pmatrix}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6680591589975dbdb6095da762f53f080026c289)













![\ vec v = \ frac {34} 5 \, \ vec b_1 + \ frac {13} 5 \, \ vec b_2 = \ frac {34} 5 \, \ begin {pmatrix} \ tfrac 3 5 \\ [1ex] \ tfrac 4 5 \ end {pmatrix} + \ frac {13} 5 \, \ begin {pmatrix} - \ tfrac {4} 5 \\ [1ex] \ tfrac 3 5 \ end {pmatrix}.](https://wikimedia.org/api/rest_v1/media/math/render/svg/511537ffc555c451aef3b6f0c1dd6cc7e0cb8f15)




























![L ^ 2 ([0.2 \ pi])](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f3f1c02125a3b161aad32d469cda6a21baff682)



![x \ in [0.2 \ pi]](https://wikimedia.org/api/rest_v1/media/math/render/svg/8cedb963595290bb4f2f9e0b1e140ba8432ccd8b)





