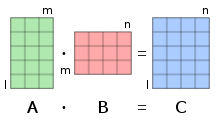
Matrix multiplication
The matrix multiplication or matrix multiplication is in mathematics a multiplicative linking of matrices . In order to be able to multiply two matrices, the number of columns in the first matrix must match the number of rows in the second matrix. The result of a matrix multiplication is then called a matrix product, matrix product or product matrix . The matrix product is again a matrix, the entries of which are determined by component-wise multiplication and summation of the entries of the corresponding row of the first matrix with the corresponding column of the second matrix.
The matrix multiplication is associative and, with the matrix addition, distributive . However, it is not commutative , that is, the order of the matrices must not be interchanged when creating the product. The set of square matrices with elements from a ring , together with the matrix addition and the matrix multiplication, form the ring of square matrices. Furthermore, the set of regular matrices over a unitary ring with the matrix multiplication forms the general linear group . Matrices, which can be converted into one another by special multiplications with regular matrices, form equivalence classes therein .
The standard algorithm for multiplying two square matrices has a cubic running time. Although the asymptotic effort can be reduced with the help of special algorithms, the determination of optimal upper and lower complexity limits for matrix multiplication is still the subject of current research.
Matrix multiplication is widely used in linear algebra . For example, the factorization of a matrix as the product of matrices with special properties is used in the numerical solution of linear systems of equations or eigenvalue problems. Furthermore, the mapping matrix of the successive execution of two linear mappings is precisely the matrix product of the mapping matrices of these maps. Applications of matrix multiplication can be found in computer science , physics and economics , among others .
Matrix multiplication was first described by the French mathematician Jacques Philippe Marie Binet in 1812.
definition
The matrix multiplication is a binary connection on the set of matrices over a ring (often the field of real numbers ), i.e. a mapping
- ,
which assigns two matrices and one more matrix . The matrix multiplication is only defined for the case that the number of columns of the matrix to the row number of the matrix matches. The number of rows in the result matrix then corresponds to that of the matrix and its number of columns to that of the matrix . Each entry of the die product is calculated using
- ,
thus by component-wise multiplication of the entries of the -th row of with the -th column of and by summing all these products. In the notation of a matrix multiplication, the painting point is often left out and written briefly instead . If the order of the factors is to be emphasized, one speaks “A is multiplied by B from the left” for the product and “A is multiplied by B from the right” for the product .
example
The two real matrices are given
- and .
Since the matrix has as many columns as the matrix has rows, the matrix multiplication can be carried out. After having two rows and two columns, the matrix product will also have two rows and columns. To calculate the first matrix element of the result matrix, the products of the corresponding entries in the first row of and the first column of are added up (the asterisks stand for elements that have not yet been calculated):
For the next element of the result matrix in the first row and second column, the first row from and the second column from are used accordingly :
This calculation scheme now continues in the second row and first column:
It is repeated for the last element in the second row and second column:
The result is the die product . Falk's scheme provides visual assistance and support for calculating the die product .
Special cases
Row vector times column vector
If the first matrix consists of only one row and the second matrix consists of only one column, the matrix product results in a matrix. If one interprets a single-row matrix as a row vector and a single-column matrix as a column vector , the standard scalar product is obtained in the case of real vectors
two vectors, where represents the vector to be transposed , both vectors must be of the same length and the result is then a real number. Each entry of a matrix product can thus be viewed as the scalar product of a row vector of the matrix with a column vector of the matrix .
Column vector times row vector
Conversely , if the first matrix consists of only one column of length and the second matrix of only one row of length , the matrix product results in a matrix. If a single-column matrix is again interpreted as a column vector and a single-row matrix as a row vector , the resulting product of vectors becomes a dyadic product
designated. Each entry in the resulting matrix is the product of an element of the first vector with an element of the second vector. The matrix product can thus be written as the sum of dyadic products of the column vectors of with the respective row vectors of .
Matrix times vector
An important special case of matrix multiplication arises when the second matrix consists of only one column. The result of the matrix multiplication is then also a single-column matrix. If a single-column matrix is again interpreted as a column vector, the matrix-vector product is obtained
- ,
where , and are. The matrix-vector product is used, for example, in the matrix notation of linear systems of equations .
Vector times matrix
Conversely, if the first matrix consists of only one row, the result is the vector-matrix product
from a row vector and a matrix again a row vector .
Square of a matrix
Multiplying a square matrix by itself results in another matrix of the same size, which is called the square of the matrix, that is:
Correspondingly, with the matrix power , i.e. the -fold product of a matrix with itself. Matrix powers are used, for example, to define the matrix exponential and the matrix logarithm . Conversely, a square matrix is called for which
holds, square root of the matrix . A matrix can have several, even an infinite number of square roots. Similarly, a matrix whose -th power gives the matrix is called the -th root of this matrix.
Block matrices
If the two matrices and have a block structure , whereby the block widths of the first matrix must match the block heights of the second matrix, then the matrix product can also be noted in blocks. The result matrix then has the block heights of the first and the block widths of the second matrix. In the case of two matrices with two by two blocks each, this results, for example
- ,
with which the result matrix also has two by two blocks.
properties
Associativity
The matrix multiplication is associative , that is, for matrices , and applies:
When multiplying several matrices, it is irrelevant in which order the partial products are formed, as long as the overall order is not changed. The following applies to the entry at the point of the resulting die product:
The matrix multiplication is also compatible with the multiplication of scalars , that is:
Distributivity
If one considers not only the matrix multiplication but also the component-wise matrix addition of two matrices , then the distributive laws are also fulfilled. That is, for all matrices applies
and for all matrices accordingly
- .
The distributive follow directly from the Distributivity of addition with multiplication in the ring on
for the first distributive law and via an analog transformation also for the second distributive law.
Non-commutativity
The commutative law, however, does not apply to matrix multiplication , that is, to and is in general
- .
For the two matrix products applies and , with which they cannot agree in terms of their dimensions. But even if and are square, both matrix products need not be the same, like the counterexample
shows. The non-commutativity of the matrix multiplication therefore even applies if the multiplication in the ring should be commutative, as is the case with numbers, for example . For special matrices, the matrix multiplication can still be commutative, see the following sections.
Further calculation rules
The following applies to the transpose of a die product
- .
The order of the multiplication is reversed by the transposition. The same applies to the adjoint of the product of complex matrices
- .
The trace of the product of two matrices and , on the other hand, is independent of the order:
With the determinant product theorem, the following also applies to the determinant of the product of two square matrices over a commutative ring:
The determinant of the product of two not necessarily square matrices can be calculated using Binet-Cauchy's theorem .
Algebraic structures
Ring of square dies
The set of square matrices of a fixed size, together with the matrix addition and the matrix multiplication, form a non-commutative ring , the matrix ring . The zero element of this ring is the zero matrix . If a unitary ring is a unitary ring , then the associated matrix ring is also unitary with the unit matrix as one element , where for all matrices
applies. In this case , the zero matrix acts as an absorbing element in the matrix ring , which means that the following applies to all matrices :
However, the ring of the square matrices is not zero divisors ; from does not necessarily follow or . Correspondingly, matrix equations must not be shortened, because it does not necessarily follow . The set of square matrices over a field forms an associative algebra with the matrix addition, the scalar multiplication and the matrix multiplication .
Group of regular matrices
The set of regular matrices over a unitary ring forms the general linear group with the matrix multiplication . The matrix inverse to the matrix is then clearly above
Are defined. For the inverse of the product of two regular matrices we then have:
As a result of the inversion, the order in the multiplication is also reversed. If regular, then the reduction rule also applies, i.e. from or then follows .
Groups of orthogonal and unitary matrices
A real square matrix is called orthogonal if
applies. With the matrix multiplication, the orthogonal matrices form the orthogonal group , a subgroup of the general linear group . Correspondingly, a complex square matrix is called unitary if
applies. With the matrix multiplication, the unitary matrices form the unitary group , a subgroup of the general linear group .
Equivalence classes of matrices
With the help of matrix multiplication, equivalence relations between matrices over a body are defined. Important equivalence relations are:
- Equivalence : Two matrices and are called equivalent if there are two regular matrices and such that it holds.
- Similarity : Two square matrices and are called similar if there is a regular matrix such that .
- Congruence : Two square matrices and are called congruent if there is a regular matrix such that .
Matrices which can be converted into one another by such multiplications with regular matrices therefore form equivalence classes .
Algorithms
Standard algorithm
In pseudocode , matrix multiplication can be implemented as follows:
function matmult(A,B,l,m,n)
C = zeroes(l,n) // Ergebnismatrix C mit Nullen initialisieren
for i = 1 to l // Schleife über die Zeilen von C
for k = 1 to n // Schleife über die Spalten von C
for j = 1 to m // Schleife über die Spalten von A / Zeilen von B
C(i,k) = C(i,k) + A(i,j) * B(j,k) // Bildung der Produktsumme
end
end
end
return C
The order of the three for loops can be interchanged as required. Since the three loops are independent of each other, the number of operations required is of the order
- .
The running time of the algorithm is therefore cubic for square matrices , i.e. of the order
- .
In matrix chain multiplication , i.e. the multiplication of three or more non-square matrices, the total number of arithmetic operations can be minimized by a clever choice of the order.
Algorithms with better complexity
Asymptotically more efficient, two square matrices can be multiplied with the Strassen algorithm . The number of multiplications required to multiply two matrices is reduced from eight to seven by cleverly combining them, which is done at the expense of additional additions. If this method is used recursively, the result is a complexity order of
- .
However, due to the constants hidden in Landau's notation, the Strassen algorithm is only worthwhile for very large matrices. The algorithm with the currently best complexity is an improvement of the Coppersmith – Winograd algorithm with a running time of the approximate order
- .
However, this algorithm is not suitable for practical use. There is a lower bound on the complexity of the matrix multiplication
- ,
since each of the elements of the output matrix has to be generated. The determination of the optimal lower and upper complexity bounds for matrix multiplication is the subject of current research.
programming
The matrix product is integrated in programming systems in different ways, in particular there is a risk of confusion with the component-wise Hadamard product . In the numerical software packages MATLAB and GNU Octave , the matrix multiplication is implemented by the asterisk operator *, so that A * Bthe matrix product results. In other programming environments such as Fortran , Mathematica , R or SciPy , however, A * Bthe Hadamard product is used to calculate. The matrix multiplication is then implemented through function calls, as matmul(A,B)in Fortran or dot(A,B)in SciPy, or by separate operators for the matrix multiplication, as .in Mathematica or %*%in R.
use
Factoring
In a sense, the inverse of matrix multiplication is factoring a given matrix as the product of two matrices and , that is, finding a representation of the shape
- .
Such a factorization is not unique, so are the matrices and placed additional requirements, such as orthogonality , symmetry or a specific occupation structure. Important decompositions of real or complex matrices of this kind are:
- the LR decomposition of a square matrix into a lower and an upper triangular matrix
- the Cholesky decomposition , a special LR decomposition of a symmetrically positive definite matrix
- the ILU decomposition , a kind of incomplete LU decomposition specifically for sparse matrices
- the QR decomposition of a matrix into an orthogonal matrix and an upper triangular matrix
- the Schur decomposition of a square matrix into three matrices: a unitary matrix, an upper triangular matrix and the inverse of the first matrix
- the singular value decomposition of a matrix into three matrices: a unitary matrix , a diagonal matrix consisting of the singular values and the adjoint of a unitary matrix
Such decomposition of matrices is often used in numerical linear algebra to solve linear systems of equations or eigenvalue problems. For example, the row and column transformations in the Gaussian elimination method can be specified as the product of elementary matrices.
Linear maps
If general and two finite-dimensional vector spaces are over the same body, then each linear mapping can be represented by a base in each of the two vector spaces using its mapping matrix. The image of a vector below the figure in the respective bases can then be used via the matrix-vector product
be determined. In geometry , for example, every rotation around the origin and every mirroring at an origin plane can be carried out in this way by such a matrix-vector product. If there is now a further vector space and a further linear mapping, then the following applies to the mapping matrix of the sequential execution of these two mappings:
The mapping matrix of a sequential execution of two linear maps is therefore the matrix product of the two associated mapping matrices. In this way, for example, each rotational mirroring can be represented as a product of a rotational matrix and a mirroring matrix. Alternatively, a linear mapping can also be carried out by vector-matrix multiplication of a line vector with the transposed mapping matrix. The execution of mappings one after the other then corresponds to a matrix multiplication from the right instead of from the left.
Applications
Applications of matrix multiplication include:
- in analysis when composing differentiable functions of several variables according to the multidimensional chain rule
- in computer graphics when performing coordinate transformations in a graphics pipeline
- in optics when calculating light rays through optical components using matrix optics
- in economics in the input-output analysis of a production as well as in the internal interlinking of materials
- in robotics when describing kinematic chains using the Denavit-Hartenberg transformation
- in electrical engineering in the two-port theory of electrical networks
- in quantum mechanics within the framework of matrix mechanics , here also for "infinitely large" matrices
Generalizations
Matrices over half rings
More generally, matrices can be viewed over a half-ring , whereby the most important properties of matrix multiplication, such as associativity and distributivity, are retained. The half-ring of the square matrices then forms accordingly . The zero matrix is again the zero element in the matrix half-ring and is also absorbent if the zero element in the underlying half-ring is absorbent. If the underlying half-ring is unitary, then the unit matrix again forms the unitary element in the matrix half-ring.
Important examples of half rings are distributive lattices , such as Boolean algebras . If one understands the elements of such a lattice as truth values , then matrices over a lattice are two-digit relations . The matrix multiplication in this case corresponds to the composition of relations .
Die categories
Algebraic structures like rings and groups whose elements are matrices are restricted to square matrices of fixed size. The matrix multiplication, however, is not so restricted. One way to overcome this limitation is to consider instead categories of matrices, each over a solid unitary ring or half-ring. The objects are natural numbers and an arrow is a matrix. The composition of arrows is given by the matrix multiplication. If matrices are also to be added, this is a pre-additive category . If matrices of all finite sizes occur, one gets an Abelian category . If there are only invertible matrices, it is a groupoid . In this case it can be interesting to allow arbitrary finite sets as objects instead of natural numbers.
similar products
In addition to the die product, there are a number of other die products:
- The Hadamard product of two matrices results in a matrix whose entries are determined simply by component-wise multiplication of the entries of the output matrices. However, it is far less significant compared to the die product.
- The Kronecker product of two matrices results in a large matrix that is created by considering all possible products of entries of the two output matrices.
- The Frobenius scalar product of two real or complex matrices results in a number that is calculated by component-wise multiplication of the entries in the output matrices and subsequent summation of all these products. In the complex case, an entry is always complex conjugated .
literature
- Tilo Arens, Frank Hettlich, Christian Karpfinger, Ulrich Kockelkorn, Klaus Lichtenegger, Hellmuth Stachel : Mathematics . 2nd Edition. Spektrum Akademischer Verlag, 2011, ISBN 3-8274-2347-3 .
- Michael Artin : Algebra . Springer, 1998, ISBN 3-7643-5938-2 .
- Gene Golub , Charles van Loan: Matrix Computations . JHU Press, 2012, ISBN 1-4214-0794-9 .
- Charles Leiserson , Ronald L. Rivest , Clifford Stein: Algorithms - An Introduction . Oldenbourg, 2010, ISBN 3-486-59002-2 .
References and comments
- ^ John J. O'Connor, Edmund F. Robertson : Jacques Philippe Marie Binet. In: MacTutor History of Mathematics archive .
- ↑ Horst Stöcker: Pocket book of mathematical formulas and modern methods . Verlag Harri Deutsch , Frankfurt am Main 2007, ISBN 978-3-8171-1811-3 , pp. 371 .
- ↑ A counterexample are two matrices, each with exactly one entry not equal to zero at the same off-diagonal position.
- ↑ Paolo D'Alberto, Alexandru Nicolau: Using recursion to boost ATLAS's performance . In: High-Performance Computing (= Lecture Notes in Computer Science ). Volume 4759. Springer, 2010, p. 142-151 , doi : 10.1007 / 978-3-540-77704-5_12 .
- ^ Virginia Vassilevska Williams: Multiplying matrices faster than coppersmith-winograd . In: STOC '12 Proceedings of the 44th symposium on Theory of Computing . ACM, 2012, p. 887-898 , doi : 10.1145 / 2213977.2214056 .
- ↑ Christoph W. Überhuber, Stefan Katzenbeisser, Dirk Praetorius: MATLAB 7: An Introduction . Springer, 2007, p. 81 .
- ↑ NumPy for Matlab Users. SciPy.org, February 22, 2014, accessed January 3, 2015 .
- ↑ Christoph Mayer, David Francas, Carsten Weber: Linear Algebra for economists . 3. Edition. GBV Fachverlage, Wiesbaden 2007, ISBN 978-3-8349-9529-2 , p. 75 f .
Web links
- Eric W. Weisstein : Matrix Multiplication . In: MathWorld (English).
- djao: Matrix operations . In: PlanetMath . (English)
- Matrix multiplication online calculator