Distributive Association

A distributive lattice is a special structure in mathematics . Compared to general associations in which the two (double-digit) operations and only the associative laws that Kommutativgesetze and the absorption laws are required, are in a distributive lattice additionally distributive for both directions . ${\displaystyle \vee }$ ${\displaystyle \wedge }$

The validity of the distributive laws makes associations more interesting. They are easier to examine because terms that occur are easier to transform and, in a certain sense, there are simple representations. Distributive associations occur very frequently, also in areas outside of mathematics. Boolean algebras are special distributive associations.

Clarification

In the following, by association V we always mean the association . ${\displaystyle \left(V,\vee ,\wedge \right)}$

A union is called a distributive union if the following applies to all : ${\displaystyle V}$ ${\displaystyle a,b,c\in V}$

• ${\displaystyle a\vee (b\wedge c)=(a\vee b)\wedge (a\vee c)}$
• ${\displaystyle a\wedge (b\vee c)=(a\wedge b)\vee (a\wedge c)}$.

Each of the two statements can be derived from the other with the help of the association axioms. It is therefore sufficient to demand the validity of one of these two distributive laws.

Every distributive association is modular , but not the other way around.

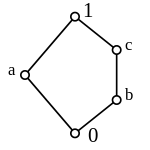
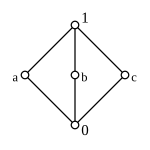
A modular lattice that is not distributive always contains the lattice , the lattice of the subgroups of Klein's group of four , as a sublattice. This results in the criterion: ${\displaystyle M_{3}}$

• If a lattice has neither a subdivision of the form nor one of the form , then it is distributive. ${\displaystyle N_{5}}$ ${\displaystyle M_{3}}$

Examples

Distributive associations can be found in many fields inside and outside of mathematics. Distributive associations are:

• any totally ordered set
• for every natural number the set of its divisors with the divisibility as an order relation ( i.e. GCD and LCM as links) ${\displaystyle n}$ ${\displaystyle T_{n}}$
• any amount association with and ${\displaystyle \cap }$ ${\displaystyle \cup }$
• any Boolean algebra
• the open sets of a topological space with as order ${\displaystyle \subseteq }$

Examples of distributive associations

Association of subsets of ordered by subsets relation ${\displaystyle \{x,y,z\}}$

Association of the divisors of 60, with GCD and LCM

${\displaystyle \mathbb {N} _{0}\times \mathbb {N} _{0}}$ with the product order

non-distributive associations

${\displaystyle N_{5}}$, the minimal non-modular association

${\displaystyle M_{3}}$, the minimal modular, non-distributive lattice:, but ${\displaystyle a\wedge (b\vee c)=a}$ ${\displaystyle (a\wedge b)\vee (a\wedge c)=0}$

Reduction rule

In a distributive lattice the reduction rule: Apply to the two equations ${\displaystyle a,b,c\in V}$

• out and follows . ${\displaystyle a\wedge b=a\wedge c}$ ${\displaystyle a\vee b=a\vee c}$ ${\displaystyle b=c}$

The example shows that this rule does not apply in any association. It is typical of distributive associations in the following sense: ${\displaystyle M_{3}}$

• If the reduction rule is valid for any choice of in a lattice V, then is distributive. ${\displaystyle a,b,c}$ ${\displaystyle V}$

Complements in distributive associations

→ Main article : Complement (lattice theory)

For a given element a of a bounded lattice one calls an element b with the property

• ${\displaystyle a\wedge b=0}$ and ${\displaystyle a\vee b=1}$

a complement of a.

While there can generally be several complementary elements to an element , the following applies:

• if there is a complement of a in a distributive lattice , then it is uniquely determined.

One designates a clearly defined complement of with or (especially in applications in logic) or . ${\displaystyle a}$ ${\displaystyle a^{c}}$ ${\displaystyle \neg a}$ ${\displaystyle {\overline {a}}}$

A distributive lattice in which every element has a (uniquely determined) complement is called Boolean algebra . ${\displaystyle a}$ ${\displaystyle \neg a}$

See also : Boolean algebra

Even in a non-distributive lattice, each element can have exactly one complement. In order to be able to deduce the distributivity, one has to demand more:

• A lattice is distributive if each element has at most one relative complement in each interval . ${\displaystyle V}$

If V is a distributive lattice and have complements, then also and have complements and it applies ${\displaystyle a,b\in V}$ ${\displaystyle a\wedge b}$ ${\displaystyle a\vee b}$

• ${\displaystyle (a\wedge b)^{c}=a^{c}\vee b^{c}}$ and ${\displaystyle (a\vee b)^{c}=a^{c}\wedge b^{c}}$

This is another formulation of de Morgan's rules .

Representation set for distributive associations

${\displaystyle T_{60}}$, the lattice of the divisors of 60 (ordered by divisibility) and the representation by the set lattice of the (irreducible) prime power elements

Distributive associations can also be characterized differently, because Birkhoff (1933) and Stone (1936) have shown:

• A lattice is distributive if and only if it is isomorphic to a set ring.

Of course, it follows from this that every distributive lattice can be embedded in a Boolean algebra.

Other properties

Every sub-lattice of a distributive lattice is distributive, but sub-lattices are not always distributive.

The homomorphic image of a distributive lattice is distributive.

The direct product of any number of distributive associations is distributive.

Complete distributivity

complete distributive association that is fully distributive but not fully distributive . It is true , but ${\displaystyle \wedge }$ ${\displaystyle \bigvee _{i\in \mathbb {N} }\left(B\wedge A_{i}\right)=A_{5}}$ ${\displaystyle B\wedge \bigvee _{i\in \mathbb {N} }A=B}$

An association is -volldistributiv when of each choice and each subset is valid ${\displaystyle \wedge }$ ${\displaystyle a\in V}$ ${\displaystyle M\subseteq V}$

${\displaystyle a\wedge \bigvee _{x\in M}x=\bigvee _{x\in M}(a\wedge x)}$.

${\displaystyle \vee }$-Full distributivity is defined in two ways.

The term full distributivity without an addition is used differently:

• It can mean that one of these two conditions is met and in the other case one speaks of dual fully distributive or explicitly uses the above designation.
• It can mean that both conditions are met.
• It can mean that the following infinite distributive law and its dual form apply

The following applies to all : ${\displaystyle \emptyset \neq I,J\subseteq V}$ ${\displaystyle \bigwedge \left\{\bigvee \left\{a_{ij}|j\in J\right\}|i\in I\right\}=\bigvee \left\{\bigwedge \left\{a_{i\varphi (i)}|i\in I\right\}|\varphi \colon I\to J\right\}}$

The following applies to all three terms:

Every fully distributive union is distributive and every finite distributive union is fully distributive.

A complete distributive union does not have to be fully distributive, as the example shows.

References and comments

1. ↑ The proof is an equation transformation. We assume that D2 is true, and want to show D1: ; Applying the second axiom: ; after Absoptionsgesetz: ; Applying the second axiom in parenthesis: ; by associative law: ; the left side corresponds to the absorption law : . The opposite direction follows dual.
   ${\displaystyle (a\vee b)\wedge (a\vee c)}$
   ${\displaystyle =((a\vee b)\wedge a)\vee ((a\vee b)\wedge c)}$
   ${\displaystyle =a\vee ((a\vee b)\wedge c)}$
   ${\displaystyle =a\vee ((a\wedge c)\vee (b\wedge c))}$
   ${\displaystyle =(a\vee (a\wedge c))\vee (b\wedge c)}$ ${\displaystyle a}$
   ${\displaystyle =a\vee (b\wedge c)}$
   
2. ↑ The proof (with several intermediate steps) can be found e.g. B. in: H. Gericke, Theory of Associations, Mannheim, 1967, p. 111
3. ↑ This is also demonstrated with a simple set of equations in which the absorption law, the distributive and the conditions are used: ; after H. Gericke, Theory of Associations, 1967, p. 114 ${\displaystyle b=b\vee (a\wedge b)=b\vee (a\wedge c)=(b\vee a)\wedge (b\vee c)}$ ${\displaystyle =(a\vee c)\wedge (b\vee c)}$ ${\displaystyle =(a\wedge b)\vee c=(a\wedge c)\vee a=c}$
4. ↑ The idea of ​​proof is that in and the reduction rule does not apply. See H. Gericke, Theory of Associations, 1967, p. 113f ${\displaystyle N_{5}}$ ${\displaystyle M_{3}}$
5. ↑ This follows directly from the reduction rule
6. ↑ G. Grätzer, Lattice Theory , 1971, p. 75
7. ↑ So z. BH Gericke, Theory of Associations, 1967, p. 114
8. ↑ This form was taken from G. Grätzer, Lattice Theory, p 118, Exercise 7.
9. ^ H. Gericke, Theory of Associations, Mannheim, 1967, p. 114 f.
10. ↑ The association without the 1 is a product of distributive. It is easy to see that the whole association is complete and distributive. The example can be found (with a slightly different Hasse diagram) in H. Gericke, Theory of Associations, Mannheim, ²1967, p. 115 ${\displaystyle \mathbb {N} \times \{0,1\}}$

literature

• Garrett Birkhoff : Lattice Theory . 3. Edition. AMS, Providence, RI 1973, ISBN 0-8218-1025-1 .
• Marcel Erné: Introduction to Order Theory . Bibliographisches Institut, Mannheim 1982, ISBN 3-411-01638-8 .
• George Grätzer: General Lattice Theory . 2nd Edition. Birkhäuser, 1998, ISBN 978-0-8176-5239-5 .
• Hans Hermes : Introduction to Association Theory . 2nd Edition. Springer, Berlin / Heidelberg 1967.